逻辑回归算法分析

    逻辑回归可以解决分类问题，属于监督学习。

一、sigmoid函数

    定义：$\sigma (x)=\frac{1}{1+e^{-x}},xϵ\mathbb{R}$，其值范围为(0, 1)，函数图形如下图所示：
            

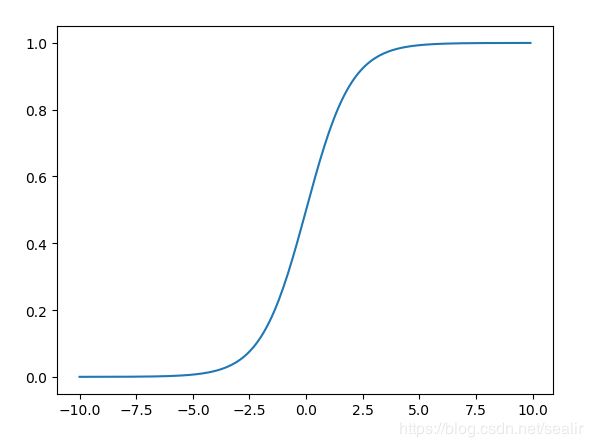
    sigmoid函数有以下的性质：

    1、${\sigma }^{\prime }(x)=\sigma (x)[1-\sigma (x)]$

    2、$\sigma (x)+\sigma (-x)=1$

    3、$[log\sigma (x){]}^{\prime }=\frac{{\sigma }^{\prime }(x)}{\sigma (x)}=1-\sigma (x)$

    4、$[log(1-\sigma (x)){]}^{\prime }=\frac{-{\sigma }^{\prime }(x)}{1-\sigma (x)}=-\sigma (x)$

---

二、二分类

    设$X=\left\{x_1,x_2,\cdots ,x_n\right\}$，可以把$X$理解成某种对象，$x_1,x_2,\cdots ,x_n$是对象的特征。

    引入分类向量$\theta =\left\{{\theta }_1,{\theta }_2,\cdots ,{\theta }_n\right\}$

    定义：$\sigma (X|\theta )=\frac{1}{1+e^{-X^T\theta }}$，在给定$\theta$时，$\sigma$函数可以将$X$映射到(0,1)之间，如果将$\sigma (x)>0.5$视为正类，$\sigma (x)<0.5$视为负类，则可以将sigmoid函数用于解决分类问题。

    在$\sigma (X|\theta )$函数中，有一个$\theta$参数，如果已知这个参数，那么该函数可以用于分类。但如果只有数据集$\left\{x_1,x_2,\cdots ,x_n\right\}$，并已经数据集的分类标签$\left\{y_1,y_2,\cdots ,y_n\right\}$，那么怎样得到参数$\theta$呢？这就是训练问题了。

---

三、逻辑回归训练

    给定样本集$X=\left\{x_1,x_2,\cdots ,x_n\right\}$和样本对应的分类标签$\left\{y_1,y_2,\cdots ,y_n\right\},y_iϵ\left\{0,1\right\}$，怎样从样本集中训练得到$\theta$参数呢？

    定义：
        极大似然函数：${\prod }_{xϵX}p(y|x,\theta )$，将其取对数后得到：

        极大对数似然函数：$\pounds ={\sum }_{xϵX}logp(y|x,\theta )$

        条件概率：$p(y|x,\theta )=\{\begin{array}{cc}\sigma (x^T\theta ),y=1& \\ & \\ 1-\sigma (x^T\theta ),y=0& \end{array}$

    怎么理解上面的极大似然呢？考虑到分类的目的，最理想的结果是：分类器将样本集分成两类，一类包含全部的正类，一类包含全部的负类。但由于样本集存在噪声，这种理想结果是不可能达到的，在这种情况下，分类器的最优结果是：将更多的真实的正类样本标记为正类，将更多的真实的负类样本标记为负类。

    所以在优化的过程中，采用梯度上升法，对$\theta$进行优化，让${\prod }_{xϵX}p(y|x,\theta )$到达极大值。

    将$p(y|x,\theta )$写成整体得：$p(y|x,\theta )=[\sigma (x^T\theta ){]}^y\cdot [1-\sigma (x^T\theta ){]}^{1-y}$，代入对数似然函数得：

    $\pounds ={\sum }_{xϵX}logp(y|x,\theta )$

       $={\sum }_{xϵX}log[\sigma (x^T\theta ){]}^y\cdot [1-\sigma (x^T\theta ){]}^{1-y}$

       $={\sum }_{xϵX}\left\{y\cdot \log [\sigma (x^T\theta )]+[1-y]\cdot log[1-\sigma (x^T\theta )]\right\}$

    函数中只有一个参数$\theta$，$\pounds$关于$\theta$的梯度：

        $\frac{\partial \pounds }{\partial \theta }=\frac{\partial }{\partial \theta }\left\{y\cdot log[\sigma (x^T\theta )]+[1-y]\cdot log[1-\sigma (x^T\theta )]\right\}$

            $=y\cdot [1-\sigma (x^T\theta )]x-[1-y]\cdot [\sigma (x^T\theta )]x$

            $=\left\{y\cdot [1-\sigma (x^T\theta )]-[1-y]\cdot [\sigma (x^T\theta )]\right\}x$

            $=[y-\sigma (x^T\theta )]x$

    按梯度上升法，$\theta$的更新可写为：

        $\theta :=\theta +\eta [y-\sigma (x^T\theta )]x$

    在机器学习中$\eta$为学习率。

    在给定样本集$\left\{X:Y\right\}=\left\{(x_1:y_1),(x_2:y_2),\cdots ,(x_n:y_n)\right\}$，训练伪代码如下：

    $FOR(x:y)=(x_1:y_1):(x_n:y_n)DO$
     {
         $\tilde{y}=\sigma (x^T\theta )$

         $e=\eta [y-\tilde{y}]x$

         $\theta :=\theta +e$
     }

    即迭代训练样本集中的每一个样本，对其进行一次二分类，将分类的误差更新到$\theta$上，当迭代完成时，$\theta$达到最优。

    当得到参数$\theta$后，便可以将其运用于分类了。