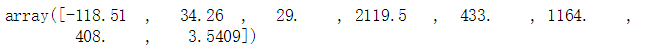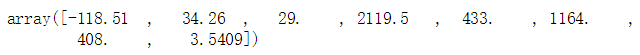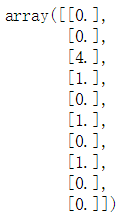character2 End-to-End Machine Learning Project （median_house_value）

一、项目概览

利用加州普查数据，建立一个加州房价模型，这个数据包含每个街区组的人口、收入的中位数、房价中位数等指标。街区组是美国调查局发布样本数据的最小地理单位（600到3000人），简称“街区”。

目标：模型利用该数据进行学习，然后根据其他指标，预测任何街区的房价中位数。

二、划定问题
 

1、应该认识到，该问题的商业目标是什么？
建立模型不可能是最终目标，而是公司的受益情况，这决定了如何划分问题，选择什么算法，评估模型的指标和微调等等。

你建立的模型的输出（一个区的房价中位数）会传递给另一个机器学习系统，也有其他信号传入该系统，从而确定该地区是否值得投资。

2、第二个问题是现在的解决方案效果如何？
比如现在截取的房价是靠专家手工估计的，专家队伍收集最新的关于一个区的信息（不包括房价的中位数），他们使用复杂的规则进行估计，这种方法浪费资源和时间，而且效果不理想，误差率大概有15%。

开始设计系统
1、划定问题：监督与否、强化学习与否、分类与否、批量学习或线上学习。

2、确定问题：

该问题是一个典型的监督学习任务，我们使用的是有标签的训练样本，每个实例都有预定的产出，即街区的房价中位数，并且是一个典型的回归任务，因为我们要预测的是一个值。

更细致一些：该问题是一个多变量的回归问题，因为系统要使用多个变量来预测结果。

最后，没有连续的数据流进入系统，没有特别需求需要对数据变动来做出快速适应，数据量不大可以放到内存中，因此批量学习就够了。
提示：如果数据量很大，你可以要么在多个服务器上对批量学习做拆分（使用Mapreduce技术），或是使用线上学习。

三、选择性能指标

回归问题的典型指标是均方根误差（RMSE），均方根误差测量的是系统预测误差的标准差，例如RMSE=50000，意味着68%的系统预测值位于实际值的50000美元误差
以内，95%的预测值位于实际值的100000美元以内，一个特征通常都符合高斯分布，即满足68-95-99.7规则，大约68%的值位于1σ内，95%的值位于2σ内，99.7%的值位于3σ内，此处的σ=50000，RMSE计算如下：

虽然大多数时候的RMSE是回归任务可靠的性能指标，在有些情况下，你可能需要另外的函数，例如，假设存在许多异常的街区，此时可能需要使用平均绝对误差（MAE）,也称为曼哈顿范数，因为其测量了城市中的两点，沿着矩形的边行走的距离：

范数的指数越高，就越关注大的值而忽略小的值，这就是为什么RMSE比MAE对异常值更敏感的原因，但是当异常值是指数分布的时候（类似正态曲线），RMSE就会表现的很好

四、核实假设

最好列出并核对迄今做出的假设，这样可以尽早发现严重的问题，例如，系统输出的街区房价会传入到下游的机器学习系统，我们假设这些价格确实会被当做街区房价使用，但是如果下游系统将价格转化为分类（便宜、昂贵、中等等），然后使用这些分类来进行判定的话，就将回归问题变为分类问题，能否获得准确的价格已经不是很重要了。

五、代码

设置

from __feature__import division,print_function,unicode_literals

import numpy as np
np.random.seed(42)

%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['xtick.labelsize'] = 12

import os
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "end_to_end_project"
def save_fig(fig_id,tight_layout = True):
    path = os.path.join(PROJECT_ROOT_DIR,"images",CHAPTER_ID,fig_id + '.png')
    print("saving figure",fig_id)
    if tight_layout:
        plt.tight_layout()
    plt.savefig(path,format = 'png',dpi = 300)

import warnings
warnings.filterwarnings(action = "ignore",module = "scipy",message = "internal gelsd")

获取数据

import os 
import tarfile 
from six.moves import urllib

DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml/master/"
HOUSING_PATH = os.path.join("datasets", "housing")
HOUSING_URL = DOWNLOAD_ROOT + "datasets/housing/housing.tgz"

def fetch_housing_data(housing_url=HOUSING_URL, housing_path=HOUSING_PATH):
    if not os.path.isdir(housing_path)
        os.makedirs(housing_path)
    tgz_path = os.path.join(housing_path, "housing.tgz")
    urllib.request.urlretrieve(housing_url, tgz_path) 
    housing_tgz = tarfile.open(tgz_path)
    housing_tgz.extractall(path=housing_path)
    housing_tgz.close()

fetch_housing_data()

加载数据并查看数据结构 

import pandas as pd
def load_housing_data(housing_path = HOUSING_PATH)：
    csv_path = os.path.join(housing_path,"housing.csv")
    return pd.read_csv(csv_path)
housing = load_housing_data()
housing.head() #查看前5行信息

 每一行表示一个街区，共有10个属性，经度、纬度、房屋年龄中位数、总房间数、总卧室数、人口数、家庭数、收入中位数、房屋价值中位数、离大海的距离。 

housing.info() #查看属性信息

数据集中有20640个实例，按机器学习的标准来说，该数据量很小，但是非常适合入门，我们注意到总房间数只有20433个非空值，也就是有207个街区缺少该值。

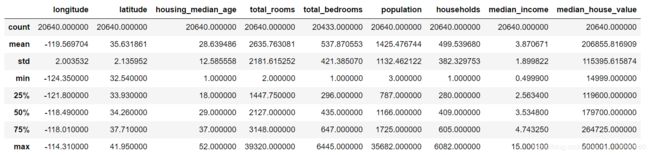
housing["ocean_proximity"].value_counts() #该属性包含几类且每类的数量

housing.describe() #属性的数学描述

卧室总数total_bedrooms为20433，所以空值被忽略了，std是标准差，揭示数值的分散度，25%的街区房屋年龄中位数小于18，50%的小于19，75%的小于37，这些值通常称为第25个百分位数（第一个四分位数）、中位数、第75个百分位数（第三个四分位数），不同大小的分位数如果很接近，说明数据很集中，集中在某个段里。 

%matplotlib inline
import matplotlib.pyplot as plt
housing.describe() #属性的数值描述
saving_fig("attribute_histogram_plots")
plt.show()

Saving figure attribute_histogram_plots

（1）收入中位不是美元，而是经过缩放调整的，过高收入的中位数会变为15，过低会变成0.5，也就是设置了阈值。

（2）房屋年龄中位数housing_median_age和房屋价值中位数median_house_value也被设了上限，房屋价值中位数是目标属性，我们的机器学习算法学习到的价格不会超过该界限。有两种处理方法：

对于设了上限的标签，重新收集合适的标签；
将这些街区从训练集中移除，也从测试集中移除，因为这会导致不准确。

（3） 这些属性有不同的量度，会在后续讨论特征缩放。

（4）柱状图多为长尾的，是有偏的，对于某些机器学习算法，这会使得检测规律变得困难，后面我们将尝试变换处理这些属性，使其成为正态分布，比如log变换。

划分训练集和测试集

#法一：自写函数通过随机直接分割数据
import numpy as np 
np.random.seed(42)
def split_train_test(data,test_ratio):
    shuffled_indices = np.random.permutation(len(data))
    test_set_size = int(len(data) * test_ratio)
    train_indices = shuffle_indices[test_set_size:]
    test_indices = shuffle_indices[:test_set_size]
    return data.iloc[train_indices],data.iloc[test_idices]
train_set,test_set = split_train_test(housing,0.2)
print(len(train_set),"train +",len(test_set),"test ")

#法二：自写函数通过hash编码+随机分割数据
import hashlib
def test_set_check(identifier,test_ratio,hash = hashlib.md5):
    return bytearray(hash(np.int64(identifier)).digest())[-1] < 256 * test_ratio
def split_train_test_by_id(data,test_ratio,id_column):
    ids = data[id_column]
    in_test_set = ids.apply(lambda id_:test_set_check(id_,test_rayio))
    return data.loc[~in_test_set],data.loc[in_test_set]

housing_with_id = hosing.reset_index()
train_set,test_set = split_train_test_by_id(housing_with_id,0.2."id")

housing_with_id["id"] = hosing["longitude"] * 1000 + housing["latitude"]
train_set,test_set = split_train_test_by_id(housing_with_id,0.2."id")

test_set.head() 

 

#法三：调用sklearn中的split_train_test_split()
from sklearn.model_selection import train_test_split
train_set,test_set = train_test_split(housing,test_size = 0.2,random_state = 42)

test_set.head()

上述为随机的取样方法，当数据集很大的时候，尤其是和属性数量相比很大的时候，通常是可行的，但是如果数据集不大，就会有采样偏差的风险，当一个调查公司想要对1000个人进行调查，不能是随机取1000个人，而是要保证有代表性，美国人口的51.3%是女性，48.7%是男性，所以严谨的调查需要保证样本也是这样的比例：513名女性，487名男性，这称为分层采样。

分层采样：将人群分成均匀的子分组，称为分层，从每个分层去取合适数量的实例，保证测试集对总人数具有代表性，如果随机采样的话，会产生严重的偏差。

若我们已知收入的中位数对最终结果的预测很重要，则我们要保证测试集可以代表整体数据集中的多种收入分类，因为收入中位数是一个连续的数值属性，首先需要创建一个收入类别属性，再仔细看一下收入中位数的柱状图。

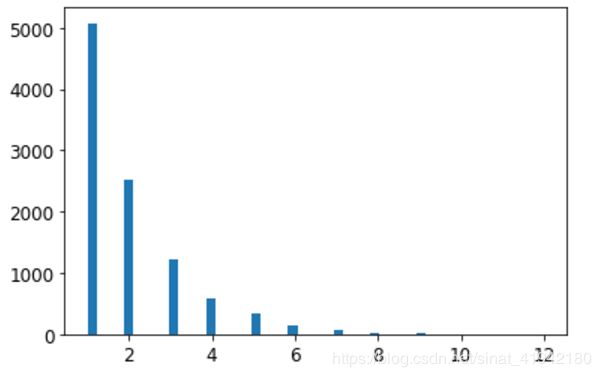
housing["median_income"].hist() 

大多数的收入的中位数都在2-5（万美元），但是一些收入中位数会超过6，数据集中的每个分层都要有足够的实例位于你的数据中，这点很重要，否则，对分层重要性的评估就会有偏差，这意味着不能有过多的分层，并且每个分层都要足够大。

随机切分的方式不是很合理，因为随机切分会将原本的数据分布破坏掉，比如收入、性别等，可以采用分桶、等频切分等方式，保证每个桶内的数量和原本的分布接近，来完成切分，保证特性分布是很重要的。

创建收入的类别属性

housing["income_cat"] = np.ceil(housing["median_income"] / 1.5)
housing["income_cat"].where(housing["income_cat"] < 5,5.0,inplace = True)
housing["income_cat"].value_counts()

housing["income_cat"].hist() 

#法四：分层抽样分割数据
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits = 1,test_size = 0.2,random_state = 42)
for train_index,test_index in split.split(housing,housing["income_cat"]):
    strat_train_set = housing.loc[train_index]
    strat_test_set = housing.loc[test_index]

strat_test_set["income_cat"].value_counts() / len(strat_test_set)

housing["income_cat"].value_counts() / len(housing)

def income_cat_proporations(data):
    return data["income_cat"].value_counts() / len(data)

train_set,test_set = train_test_split(housing,test_size = 0.2,random_state = 42)

compare_props = pd.DataFrame({
        "Overall":income_cat_proporations(housing),
        "Stratified":income_cat_proporations(strat_test_set),
        "Random":income_cat_proporations(test_set),
}).sort_index()

compare_props["Rand,%error"] = 100 * compare_props["Random"] / compare_props["Overall"] - 100
compare_props["Strat,%error"] = 100 * compare_props["Stratified"] / compare_props["Overall"] - 100

compare_props

for set_ in(strat_train_set,strat_test_set):
    set_.drop("income_cat",axis = 1,inplace = True)

数据可视化并发现规律

housing = strat_train_set.copy()
housing.plot(kind = "scatter",x = "longitude",y = "latitude")
save_fig("bad_visualization_plot")

housing.plot(kind = "scatter",x = "longitude",y = "latitude",alpha = 0.1)
save_fig("better_visualization_plot")

housing.plot(kind = "scatter",x = "longitude",y = "latitude",alpha = 0.4,
    s = housing["population"]/100,label = "population",figsize = (10,7),
    c = "median_house_value",cmap = plt.get_cmap("jet"),colorbar = True,
    sharex = False)
plot.legend()
save_fig("housing_prices_scatterplot")

import matplotlib.image as mping
california_img = mping.imread(PROJECT_ROOT_DIR + '/images/end_to_end_project/california.png')
ax = housing.plot(kind = "scatter",x = "longitude",y = "latitude",alpha = 0.4,
    s = housing["population"]/100,label = "population",figsize = (10,7),
    c = "median_house_value",cmap = plt.get_cmap("jet"),colorbar = True,
    sharex = False)
plt.imshow(california_img,extent = [-124.55,-113.80,32.45,42.05],alpha = 0.5,
    cmap = plt.get_cmap("jet"))
plt.ylabel("Latitude",fontsize = 14)
plt.xlabel("Longtitude",fontsize = 14)

#绘制右侧Median House Value的颜色条
prices = housing["median_house_value"]
tick_values = np.linspace(prices.min(),prices.max(),11)
cbar = plt.colorbar()
cbar.ax.set_yticklabels(["$%dk"%(round(v / 1000)) for v in tick_values],fontsize = 14)
cbar.set_label('Median House Value',fontsize = 16)

plot.legend(fontsize = 16)
save_fig("califorina_housing_prices_plot")
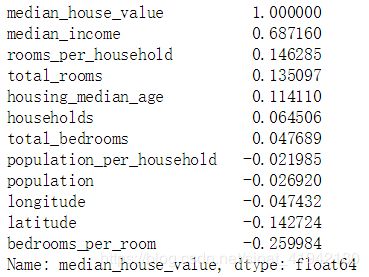
plt.show()

corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending = False)

from pandas.plotting import scatter_matrix
attributes = ["median_house_value","median_income","total_rooms","housing_median_age"]
scatter_matrix(housing[attributes],figsize = (12,8))
save_fig("scatter_matrix_plot")

housing.plot(kind = "scatter",x = "median_income",y = "median_house_value",alpha = 0.1)
plt.axis([0,16,0,550000])
save_fig("income_vs_house_value_scatterplot")

housing["rooms_per_household"] = housing["total_rooms"] / housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"] / housing["total_rooms"]
housing["population_per_household"] = housing["population"] / housing["households"]
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending = False)

housing.plot(kind = "scatter",x = "rooms_per_household",y = "media_house_value",alpha = 0.2)
plt.axis([0,5,0,520000])
plt.show()

housing.describe()

准备ML算法的数据

数据处理分为两类：

（1）数值型数据

缺失值填充（Imputer）、属性融合（Pipeline）、归一化处理（Standard）

（2）类别型数据

One-hot编码

housing = strat_train_set.drop("median_house_value",axis = 1)
housing_labels = strat_train_set["median_house_value"].copy()

sample_incomplete_rows = housing[housing.isnull().any(axis = 1)].head()
sample_incomplete_rows

处理缺失值 

sample_incomplete_rows.dropna(subset = ["total_bedrooms"])

sample_incomplete_rows.drop("total_bedrooms",axis = 1)

median = housing["total_bedrooms"].median()
sample_incomplete_rows["total_bedrooms"].fillna(median,inplace = True)
sample_incomplete_rows

try:
    from sklearn.impute import SimpleImputer
except ImportError:
    from sklearn.preprocessing import Imputer as SimpleImputer

imputer = SimpleImputer(strategy = "median") 

housing_num = housing.drop('ocean_proximity',axis = 1)#删除文本属性
imputer.fit(housing_num)  #计算中位数

imputer.statistics_
#每个属性的中位数 

housing_num.median().values #手工计算的每个属性的中位数 

X = imputer.transform(housing_num) #将缺失值替换成中位数
housing_tr = pd.DataFrame(X,columns = housing_num.columns,index = list(housing.index.values))
housing_tr.loc[sample_incomplete_rows.index.values]

imputer.strategy

housing_tr = pd.DataFrame(X,columns = housing_num.columns,index = housing_num.index))
housing_tr.head()

将文本信息转化为类别信息 

housing_cat = housing[['ocean_proximity']]
housing_cat.head(10)

try:
    from sklearn.preprocessing import OrdinalEncoder
except ImportError:
    from future_encoders import OrdinalEncoder

ordinal_encoder = OrdinalEncoder()
housing_cat_encoded = ordinal_encoder.fit_transform(housing_cat)
housing_cat _encoded[:10]

ordinal_encoder.categories_

try:
    from sklearn.preprocessing import OrdinalEncoder
    from sklearn.preprocessing import OneHotEncoder
except ImportError:
    from future_encoders import OneHotEncoder

cat_encoder = OneHotEncoder()
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)
housing_cat _1hot

housing_cat_1hot.toarray()

cat_encoder = OneHotEncoder(sparse = False)
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)
housing_cat_1hot  

cat_encoder.categories_ 

自定义参数转换器

from sklearn.base import BaseEstimator,TransformerMixin

rooms_ix,bedrooms_ix,population_ix,household_ix = 3,4,5,6

class CombinedAttributesAdder(BaseEstimator,TransformerMixin):
    def __init__(self,add_bedrooms_per_room = True):
        self.add_bedrooms_per_room = add_bedrooms_per_room
    def fit(self,X,y = None):
        return self
    def transform(self,X,y = None):
        rooms_per_household = X[:,rooms_ix] / X[:,household_ix]
        population_per_household = X[:,population_ix] / X[:,household_ix]
        if self.add_bedrooms_per_room:
            bedrooms_per_room =  X[:,bedrooms_ix] / X[:,rooms_ix]
            return np.c_[X,rooms_per_household,population_per_household,bedrooms_per_room]
        else:
            return np.c_[X,rooms_per_household,population_per_household]

attr_adder = CombinedAttributesAdder(add_bedrooms_per_room = False)

housing_extra_attribs = attr_adder.transform(housing.values)

housing_extra_attribs = pd.DataFrame(
        housing_extra_attribs,
        columns = list(housing.columns)+["rooms_per_household","population_per_household"])

housing_extra_attribs.head()

构建流水线

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

num_pipeline = Pipeline([
    ('imputer',Imputer(strategy = "median")),
    ('attribs_adder',CombineAttributesAdder()),
    ('std_scaler',StandardScaler()),
    ])
housing_num_tr = num_pipeline.fit_transform(housing_num)
housing_num_tr

try:
    from sklearn.compose import ColumnTransformer
expect ImportError:
    from future_encoders import ColumnTransformer

num_attribs = list(housing_num)
cat_attribs = ["ocean_proximity"]
full_pipeline = ColumnTransformer([
        ("num",num_pipeline,num_attribs),    
        ("cat",OneHotEncoder(),cat_attribs),
    ])
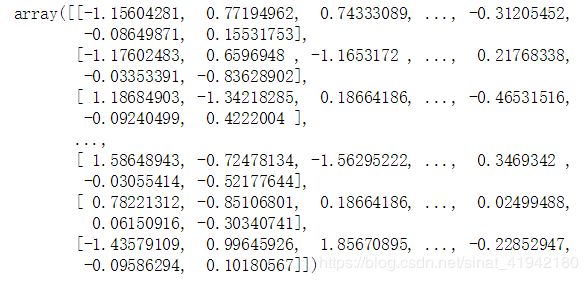
housing_prepares = full_pipeline.fit_transform(housing)

housing_prepared

housing_prepared.shape

from sklearn.base import BaseEstimator,TransformerMixin
#rooms_ix,bedrooms_ix,population_ix,household_ix = 3,4,5,6
class OldDataFrameSelector(BaseEstimator,TransformerMixin):
    def __init__(self,attribute_names):
        self.attribute_names = attribute_names
    def fit(self,X,y = None):
        return self
    def transform(self,X):
            return X[self.attribute_names].values


num_attribs = list(housing_num)
cat_attribs = ["ocean_proximity"]
old_num_pipeline = Pipeline([
    ('selector',OldDataFrameSelector(num_attribs)),
    ('imputer',Imputer(strategy = "median")),
    ('attribs_adder',CombineAttributesAdder()),
    ('std_scaler',StandardScaler()),
    ])
old_cat_pipeline = Pipeline([
        ('selector',OldDataFrameSelector(cat_attribs)),    
        ("cat_encoder",OneHotEncoder(sparse = False)),
    ])


from sklearn.pipeline import FeatureUnion
old_full_pipeline = FeatureUnion(transformer_list = [
        ("num_pipeline",old_num_pipeline),
        ("cat_pipeline",old_cat_pipeline), 
    ])


old_housing_prepared = nold_full_pipeline.fit_transform(housing)
old_housing_prepared

np.allclose(housing_prepared,old_housing_prepared)

选择模型并进行

#模型一：线性回归
from sklearn.linear_model import  LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(housing_prepared,housing_labels) 

some_data = housing.iloc[:5]
some_labels = housing_labels.iloc[:5]
some_data_prepared = full_pipeline.transform(some_data)
print("Predictions:",lin_reg.predict(some_data_prepared))

print("Labels:",list(some_labels))

some_data_prepared

from sklearn.metrics import mean_squared_error
housing_predictions = lin_reg.predict(housing_prepared)
lin_mse = mean_squared_error(housing_labels,housing_predictions)
lin_rmse = np.sqrt(lin_mse)
lin_rmse

from sklearn.metrics import mean_absolute_error
lin_mae = mean_absolute_error(housing_labels,housing_predictions)
lin_mae

#模型二：决策树
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor(random_state = 42)
tree_reg.fit(housing_prepared,housing_labels)

housing_predictions = tree_reg.predict(housing_prepared)
tree_mse = mean_squared_error(housing_labels,housing_predictions)
tree_rmse = np.sqrt(tree_mse)
tree_rmse

微调模型

from sklearn.model_selection import cross_val_score
scores = cross_val_score(tree_reg,housing_labels,scoring = "neg_mean_squared_error",cv = 10)
tree_rmse_scores = np.sqrt(-scores)

def display_scores(scores):
    print("Scores:",scores)
    print("Mean:",scores.mean())
    print("Standard deviation:",scores.std())
display_scores(tree_rmse_scores)

lin_scores = cross_val_score(lin_reg,housing_prepared,housing_labels,
    scoring = "neg_mean_squared_error",cv = 10)
lin_rmse_scores = np.sqrt(-scores)

display_scores(lin_rmse_scores)

#模型三：随机森林
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor(random_state = 42)
forest_reg.fit(housing_prepared,housing_labels) 

housing_predictions = forest_reg.predict(housing_prepared)
forest_mse = mean_squared_error(housing_labels,housing_predictions)
forest_rmse = np.sqrt(forest_mse)
forest_rmse

from sklearn.model_selection import cross_val_score
forest_scores = cross_val_score(forest_reg,housing_prepared,housing_labels,
    scoring = "neg_mean_squared_error",cv = 10)
forest_rmse_scores = np.sqrt(-forest_scores)

display_scores(forest_rmse_scores)

scores = cross_val_score(lin_reg,housing_prepared,housing_labels,
    scoring = "neg_mean_squared_error",cv = 10)
rmse_scores = np.sqrt(-scores)
pd.Series(rmse_scores).describe()

#模型四：SVM
from sklearn.svm import SVR
svm_reg = SVR(kernel = "Linear")
svm_reg.fit(housing_prepared,housing_labels) 
housing_predictions = svm_reg.predict(housing_prepared)
svm_mse = mean_square_error(housing_labels,housing_predictions)
svm_rmse = np.sqrt(svm_mse)
svm_rmse

调参 

网络搜索和随机搜索，实际项目中应该是先通过随机搜索确定一个较小的范围之后再应用网络搜索对指定范围进行详细的搜索。
网络搜索是当已经将参数组合确定在一个小范围时候使用的。参数范围较大的情况下应该用Randomized Search随机搜索，RandomizedSearchCV。这个类类似于grid_search，但是它不会搜索所有可能的组合，只是随机选择其中的一部分。

网格搜索方法有两个好处：

（1）随机1000次会对1000种不同的参数组合进行测试；

（2）只需要设置迭代次数就可以控制计算。

from sklearn.model_selection import GridSearchCV
param_grid = [
    {'n_estimators': [3,10,30],'max_features':[2,4,6,8]},
    {'bootstrap': [False],'n_estimators': [3,10],'max_features':[2,3,4},
    ]
forest_reg = RandomForestRegressor(random_state = 42)
grid_search = GridSearchCV(forest_reg,param_grid,cv = 5,
    scoring = 'neg_mean_squared_error',return_train_score = True)
grid_search.fit(housing_prepared,housing_labels) 

grid_search.best_params_

grid_search.best_estimator_

cvres = grid_search.cv_results_
from mean_score,params in zip(cvres["mean_test_score"],cvres["params"])
    print(np.sqrt(- mean_socre),params)

pd.DataFrame(grid_search,cv_results_)

from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint
param_distribs = {'n_estimators': randint(low = 1,high = 200),
                  'max_features':randint(low = 1,high = 8),}
forest_reg = RandomForestRegressor(random_state = 42)
rnd_search = RandomizedSearchCV(forest_reg,
                   param_distributions = param_distribs,
                   n_iter = 10,cv = 5,
                   scoring = 'neg_mean_squared_error',
                   random_state = 42)
rnd_search.fit(housing_prepared,housing_labels) 

cvres = rnd_search.cv_results_
from mean_score,params in zip(cvres["mean_test_score"],cvres["params"])
    print(np.sqrt(- mean_socre),params)

feature_importances = grid_search.best_estimator_.feature_importances
feature_importances

extra_attribs = ["rooms_per_hhold","pop_per_hhold","bedrooms_per_room"]
cat_encoder = full_pipeline.name_transformers_["cat"]
cat_one_hot_attribs = list(cat_encoder.categories_[0])
attributes = num_attribs + extra_attribs + cat_one_hot_attribs
sorted(zip(featere_importances,attributes),reverse = True)

final_model = grid_search.best_estimator_

X_test = strat_test_set.drop("median_house_value",axis = 1)

y_test = strat_test_set["median_house_value"].copy()


X_test_prepared = full_pipeline.transform(X_test)
final_predictions = final_model.predict(X_test_prepared)

final_mse = mean_squared_error(y_test,final_predictions)
final_rmse = np.sqrt(final_mse) 
final_rmse

为测试的RMSE计算95%置信区间

from scipy import stats
confidence = 0.95
squared_errors = (final_predictions - y_test) ** 2
mean = squared_error.mean()
m = len(squared_errors)

np.sqrt(stats.t.interval(confidence,m-1,
                         loc = np.mean(squared_errors),
                         scale = stats.sem(squared_error))
        )

tscore = stats.t.ppf((1 + confidence) / 2,df = m - 1)
tmargin = tscore * squared_errors.std(ddof = 1) / np.sqrt(m)
np.sqrt(mean - tmargin),np.sqrt(mean + tmargin)

zscore = stats.norm.ppf((1 + confidence) / 2)
zmargin = zscore * squared_errors.std(ddof = 1) / np.sqrt(m)
np.sqrt(mean - zmargin),np.sqrt(mean + zmargin)

额外材料

集准备与预测为一体的流水线

full_pipeline_with_predictor = Pipeline([
        ("preparation",full_pipeline),
        ("linear",LinearRegression())       
        ])

full_pipeline_with_predictor.fit(housing,housing_labels)
full_pipeline_with_predictor.predict(some_data)

使用joblib保存模型

my_model = full_pipeline_with_predictor
from sklearn.externals import joblib
joblib.dump(my_model,"my_model.pkl")
my_model_loaded = joblib.load("my_model.pkl")

RandomizedSearchCV的Scipy示例描述

from scipy.stats import geom,expon
geom_distrib = geom(0.5).rvs(10000,random_state = 42)
expon_distrib = expon(scale = 1).rvs(10000,random_state = 42)
plt.hist(geom_distrib,bins = 50)
plt.show()
plt.hist(expon_distrib,bins = 50)
plt.show()

课后练习

1.使用不同的超参数，如kernel=“linear”（具有C超参数的多种值）或kernel=“rbf”（C超参数和gamma超参数的多种值），尝试一个支持向量机回归器，不用担心现在不知道这些超参数的含义。最好的SVR预测期是如何工作的？

from sklearn.model_selection import GridSearchCV
param_grid = [
              {'kernel': ['linear'],'C':[10.,30.,100.,300.,1000.,3000.,10000.,30000.0]},
              {'kernel': ['rbf'],'C':[1.0,3.0,10.,30.,100.,300.,1000.0],
               'gamma':[0.01,0.03,0.1,0.3,1.0,3.0]},
]

svm_reg = SVR()
grid_search =GridSearchCV(svm_reg,param_grid,cv = 5,
               scoring = 'neg_mean_squared_error',verbose = 2,
                n_jobs = 4)
grid_search.fit(housing_prepared,housing_labels)

negative_mse = grid_search.best_score_
rmse = np.sqrt(-negative_mse)
rmse

grid_search.best_params_

分析： 通过网格搜索可以看出，线性核的SVR比rbf核更适合。而且需要注意的是C的值是候选参数中最大的，所以我们可以尝试更大的C值，因为C越大越好。

2.尝试用RandomizedSearchCV替换GridSearchCV

scipy统计分析库（含各种概率分布函数）

from sklearn.model_selection import RandomizedSearchCV
param_distribs = {
          'kernel': ['linear','rbf'],
          'C':reciprocal(20,200000),
          'gamma':expon(scale = 1.0),
}

svm_reg = SVR()
rnd_search =RandomizedSearchCV(svm_reg,
                               param_distributions = param_distribs,
                               n_iter = 50,cv = 5,
                               scoring = 'neg_mean_squared_error',
                               verbose = 2,n_jobs = 4,random_state = 42)
rnd_search.fit(housing_prepared,housing_labels)

negative_mse = rnd_search.best_score_
rmse = np.sqrt(-negative_mse)
rmse

rnd_search.best_params_

这次搜索为rbf核找到了一组很好的超参数。在相同的时间内，随机搜索比网格搜索更容易找到超参数。

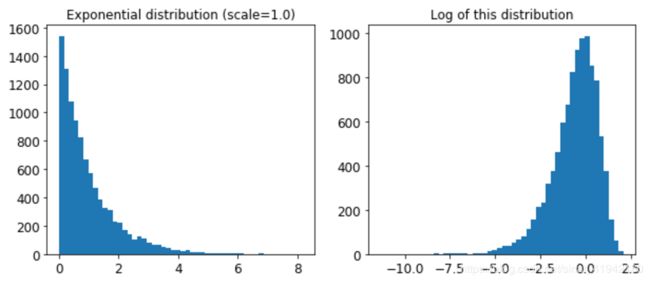
看看使用的指数分布，scale=1.0。注意，有些样本比1.0大得多或小得多，但是当查看分布的日志时，可以看到大多数值实际上大致集中在exp(-2)到exp(+2)的范围内，大约是0.1到7.4。

expon_distrib = expon(scale = 1.)
samples =expon_distrib.rvs(10000,random_state = 42)
plt.figure(figsize = (10,4))
plt.subplot(121)
plt.title("Exponential distribution (scale = 1.0)")
plt.hist(samples,bins = 50)
plt.show()
plt.subplot(122)
plt.title("Log of this distribution")
plt.hist(np.log(samples),bins = 50)
plt.show()

C的选取是从给定范围的均匀分布内选取的，所以2张图看起来差别不是很大。当不知道目标比例时，这种分布非常有用。

这里C和gamma分别是用reciprocal分布和指数分布去采样的。模拟采样过程：

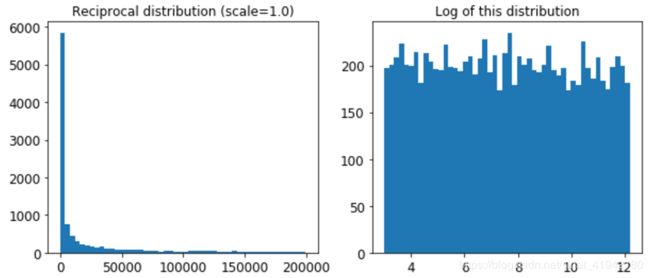
reciprocal_distrib = reciprocal(20,200000)
samples =reciprocal_distrib.rvs(10000,random_state = 42)
plt.figure(figsize = (10,4))
plt.subplot(121)
plt.title("Reciprocal distribution (scale = 1.0)")
plt.hist(samples,bins = 50)
plt.subplot(122)
plt.title("Log of this distribution")
plt.hist(np.log(samples),bins = 50)
plt.show()

当你不知道的规模hyperparameter应该是什么，reciprocal的分布是非常有用的。（事实上,正如你可以看到在右边的图,在给定的范围内，所有的标度都是等可能的,reciprocal的分布是一个 对数均匀分布)，而当您知道(或多或少)超参数的标度时，指数分布是最好的。）

3.尝试再准备流水线中添加一个转换器，从而只选出最重要的属性

首先，实现选择TopK的方法。

from sklearn.base import BaseEstimator,TransformerMixin

def indices_of_top_k(arr,k):
    return np.sort(np.argpartition(np.array(arr),-k)[-k:])

class TopFeatureSelector(BaseEstimator,TransformerMixin):
    def __init__(self,feature_importances,k):
        self.feature_importances = feature_importances
        self.k = k
    def fit(self,X,y = None):
        self.feature_indices = indices_of_top_k(self.feature_importances,self.k)
        return self
    def transform(self,X):
        return X[:,self.feature_indices_]

注意:这个特性选择器假设您已经以某种方式计算了特性的重要性(例如使用RandomForestRegressor)。您可能想直接在TopFeatureSelector的fit()方法中计算它们，但是这可能会降低网格/随机搜索的速度，因为必须为每个超参数组合计算特征的重要性(除非实现某种缓存)。

让我们来定义我们想要保留的顶级功能的数量,并看看前k个特征的索引:

k = 5
top_k_feature_indices = indices_of_top_k(feature_importances,k)
top_k_feature_indices

np.array(attributes)[top_k_feature_indices]

让我们再次检查这些确实是前k个功能:

sorted(zip(featere_importances,attributes),reverse = True)

现在，让我们创建一个新的管道来运行前面定义的准备管道，并添加top k特性选择:

preparation_and_feature_selection_pipeline = Pipeline([
        ("preparation",full_pipeline),
        ("feature_selection",
TopFeatureSelector(feature_importances,k))       
        ])

housing_prepared_top_k_features = preparation_and_feature_selection_pipeline.fit_transform(housing)
housing_prepared_top_k_features[0:3]

现在让我们再次检查这些确实是前k个功能:

housing_prepared[0:3,top_k_feature_indices]

4.尝试创建一个单独的流水线用来完成完整的数据准备和最终预测

prepare_select_and_predict_pipeline = Pipeline([
        ("preparation",full_pipeline),
        ("feature_selection",
TopFeatureSelector(feature_importances,k)),
        ('svm_reg',SVR(**rnd_search.best_params_))       
        ])

prepare_select_and_predict_pipeline.fit(housing,housing_labels)

让我们在几个实例中尝试完整的流水线:

some_data = housing.iloc[:4]
some_labels = housing_labels.iloc[:4]
print("Predictions:\t",prepare_select_and_predict_pipeline.predict(some_data))
print("Labels:\t\t",list(some_labels))

嗯，整个流程似乎运作良好。当然，这些预测并不是异想天开:如果我们使用之前发现的最好的RandomForestRegressor，而不是最好的SVR，预测结果会更好。

5.使用GridSearchCV自动搜索一些准备选项

param_grid = [    
    {'preparation_num_imputer_strategy':['mean','median','most_frequent'],
     'feature_selection_k':list(range(1,len(feature_importances) + 1))}
]
grid_search_prep =GridSearchCV(prepare_select_and_predict_pipeline,param_grid,cv = 5,
               scoring = 'neg_mean_squared_error',verbose = 2,
                n_jobs = 4)
grid_search_prep.fit(housing,housing_labels)

grid_search_prep.best_params_

最好的估算策略是最频繁的，显然几乎所有的特征都是有用的(16个中的15个)。最后一个(岛)似乎只是增加了一些噪音。