【算法导论】最大流算法
最大流问题就是在容量容许的条件下,从源点到汇点所能通过的最大流量。
1 流网络
网络流G=(v, E)是一个有向图,其中每条边(u, v)均有一个非负的容量值,记为c(u, v) ≧ 0。如果(u, v) ∉ E则可以规定c(u, v) = 0。网络流中有两个特殊的顶点,即源点s和汇点t。
与网络流相关的一个概念是流。设G是一个流网络,其容量为c。设s为网络的源点,t为汇点,那么G的流是一个函数f:V×V →R,满足一下性质:
容量限制:对所有顶点对u,v∈V,满足f(u, v) ≦ c(u, v);
反对称性:对所有顶点对u,v∈V,满足f(u, v) = - f(v, u);
流守恒性:对所有顶点对u∈V-{s, t},满足Σv∈Vf(u,v)=0。
本文开始讨论解决最大流问题的Ford-Fulkerson方法,该方法也称作“扩充路径方法”,该方法是大量算法的基础,有多种实现方法。
Ford-Fulkerson算法是一种迭代算法,首先对图中所有顶点对的流大小清零,此时的网络流大小也为0。在每次迭代中,通过寻找一条“增广路径”(augument path)来增加流的值。增广路径可以看作是源点s到汇点t的一条路径,并且沿着这条路径可以增加更多的流。迭代直至无法再找到增广路径位置,此时必然从源点到汇点的所有路径中都至少有一条边的满边(即边的流的大小等于边的容量大小)。
其基本思想为:
给定一个流网络G和一个流,流的残留网Gf拥有与原网相同的顶点。原流网络中每条边将对应残留网中一条或者两条边,对于原流网络中的任意边(u, v),流量为f(u, v),容量为c(u, v):
如果f(u, v) > 0,则在残留网中包含一条容量为f(u, v)的边(v, u);
如果f(u, v) < c(u, v),则在残留网中包含一条容量为c(u, v) - f(u, v)的边(u, v)。
残留网允许我们使用任何广义图搜索算法来找一条增广路径,因为残留网中从源点s到汇点t的路径都直接对应着一条增广路径。在关于基本思想的解读方面,算法导论的理论讲解令我一知半解,后来在网上找到了下面的图解过程,个人觉得十分清晰易懂,因此借鉴如下:
以图为例,具体分析增广路径及其相应残留网,如图(a~d)。
(a)原始图流网络,每条边上的流都为0。因为f(u, v) = 0 < c(u, v),则在残留网中包含容量为c(u, v)的边(u, v),所以此时残留图中顶点与原始流网络相同,边也与原始流网络相同,并且边的容量与原始流网络相同。
在残留网中可以找到一条增广路径
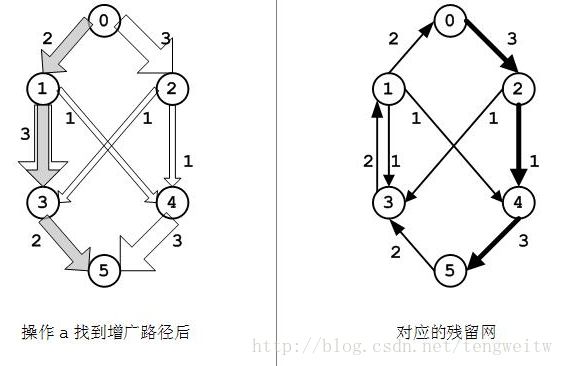
(b)在操作(a)之后,路径
f(0, 1) > 0,在残留图中有容量为2的边(1, 0);
c(1, 3) > f(1, 3) > 0,在残留图中有容量为1的边(1, 3)和容量为2的边(3, 1);
f(3, 5) > 0,在残留图中有容量为2的边(5, 3).
在残留网中可以找到一条增广路径
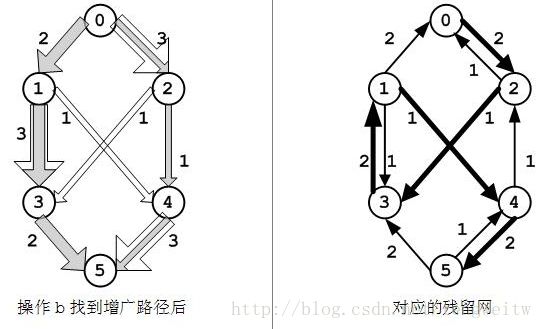
(c)在操作(b)之后,路径
c(0, 2) > f(0, 2) > 0,在残留图中有容量为2的边(0, 2)和容量为1的边(2, 0);
f(2, 4) > 0,在残留图中有容量为1的边(4, 2);
c(4, 5) > f(4, 5) > 0,在残留图中有容量为2的边(4, 5)和容量为1的边(5, 4).
进一步在残留网中可以找到一条增广路径
(d)在操作(c)之后,路径
c(0, 2) > f(0, 2) > 0,在残留图中有容量为1的边(0, 2)和容量为2的边(2, 0);
f(2, 3) > 0,在残留图中有容量为1的边(3, 2);
c(3, 1) > f(3, 1) > 0,在残留图中有容量为1的边(3, 1)和容量为2的边(1, 3);
f(1, 4) > 0,在残留图中有容量为1的边(4, 1);
c(4, 5) > f(4, 5) > 0,在残留图中有容量为1的边(4, 5)和容量为2的边(5, 4);
此时残留图中无法再找到顶点0到顶点5的路径,则迭代结束,我们认为图d中即为寻找到的最大流(该结论可以由最大流最小割定理证明)。
最大流最小割定理:一个网中所有流中的最大值等于所有割中的最小容量。并且可以证明一下三个条件等价:
f是流网络G的一个最大流;
残留网Gf不包含增广路径;
G的某个割(S, T),满足f(S, T) = c(S, T).
寻找增广路径方法的影响
增广路径事实上是残留网中从源点s到汇点t的路径,可以利用图算法中的任意一种被算法来获取这条路径,例如BFS,DFS等。其中基于BFS的算法通常称为Edmonds-Karp算法,该算法是“最短”扩充路径,这里的“最短”由路径上的边的数量来度量,而不是流量或者容量。
这里所选的路径寻找方法会直接影响算法的运行时间,例如,对图采用DFS的方法搜索残留网中的增广路径。图(b)中是第一次搜索得到的增广路径为
如果换一种方法对残留网中的进行遍历将会很快求得流网络的最大流。如图,第一次在顶点1搜索下一条边时,不是选择边(1, 2)而是选择容量更大的边(1, t);第二次在顶点2处搜索下一条边时,选择边(2, t)。这样只要两次遍历即可求解最大流。可见,在残留网中搜索增广路径的算法直接影响Ford-Fulkerson方法实现的效率。
下面我采用BFS算法来寻找增广路径,具体的程序实现如下:
#include
#define N 6 //顶点数
/********************************************************\
函数功能:从残留网络中找到从源点s到汇点t的增广路径
输入:残留网络矩阵、记录前一顶点的矩阵
输出:0表示未找到路径,1表示找到了路径
\********************************************************/
int search(int dist1[N][N],int vertex[N])
{
int queue[20]={-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1};//初始化,-1作为标记
int flag[N]={0};//标记顶点是否被访问过
int front=0;//队列头指针
int rear=0;//队列尾指针
int temp=0;
int i;
queue[rear]=0;//将源点入队列
flag[0]=1;
rear++;
while(queue[front]!=-1)//队列不为空
{
temp=queue[front];//取队头元素
for(i=0;i0)//更改残余图
dist1[j][i]=dist1[i][j];
dist1[i][j]=dist1[i][j]-min;
dist[i][j]=dist[i][j]+min-dist[j][i];//更改原始流网路
if(dist[i][j]<0)
{
dist[j][i]=-dist[i][j];
dist[i][j]=0;
}
j=i;
i=vertex[i];
}
printf("原始流网络矩阵:\n");
for(int i=0;i 显示结果如下:
原始流网络矩阵:
0 2 0 0 0 0
0 0 0 2 0 0
0 0 0 0 0 0
0 0 0 0 0 2
0 0 0 0 0 0
0 0 0 0 0 0
残留网络矩阵:
0 0 3 0 0 0
2 0 0 1 1 0
0 0 0 1 1 0
0 3 0 0 0 0
0 0 0 0 0 3
0 0 0 2 0 0
原始流网络矩阵:
0 2 1 0 0 0
0 0 0 2 0 0
0 0 0 0 1 0
0 0 0 0 0 2
0 0 0 0 0 1
0 0 0 0 0 0
残留网络矩阵:
0 0 2 0 0 0
2 0 0 1 1 0
3 0 0 1 0 0
0 3 0 0 0 0
0 0 1 0 0 2
0 0 0 2 3 0
原始流网络矩阵:
0 2 2 0 0 0
0 0 0 1 1 0
0 0 0 1 1 0
0 0 0 0 0 2
0 0 0 0 0 2
0 0 0 0 0 0
残留网络矩阵:
0 0 1 0 0 0
2 0 0 3 0 0
2 0 0 0 0 0
0 2 1 0 0 0
0 1 1 0 0 1
0 0 0 2 2 0
最大流为4
请按任意键继续. . .
注:如果程序出错,可能是使用的开发平台版本不同,请点击如下链接: 解释说明
原文:http://blog.csdn.net/tengweitw/article/details/17766133
作者:nineheadedbird