《再学一周光线追踪》 学习 二 绑定界体层次
蒙特卡洛光线追踪技术系列 见 蒙特卡洛光线追踪技术
这部分是迄今为止我们正在研究的光线跟踪器中最困难和最复杂的部分。我把它放在第二章中,这样代码可以运行得更快,而且因为它重构了一些hitable,当我添加矩形和框时,我们就不必回去重构它们了。
光线与物体的相交是光线跟踪器的主要时间瓶颈,并且时间与物体的数量成线性关系。但它是对同一模型的重复搜索,所以我们应该能够使用二分搜索的速度来进行对数级复杂度的搜索。因为我们在同一个模型上发送数百万到数十亿条射线,我们可以做一个排序模型的模拟,然后每个射线交叉点可以是一个次线性搜索。两种最常见的排序方法是1)划分空间,2)划分对象。对于大多数模型来说,后者通常更容易编写代码,运行速度也同样快。
在一组基本体上包围体的关键思想是找到一个完全包围(包围)所有对象的体。例如,假设计算了10个对象的边界球体。任何错过边界球体的光线肯定会错过所有十个对象。如果光线击中边界球体,则可能会击中十个对象之一。所以边界代码的形式总是:
if (ray hits bounding object)
return whether ray hits bounded objects
else
return false关键的一点是我们将对象划分为子集。我们不分屏幕和音量。任何对象都只在一个边界体中,但边界体可以重叠。
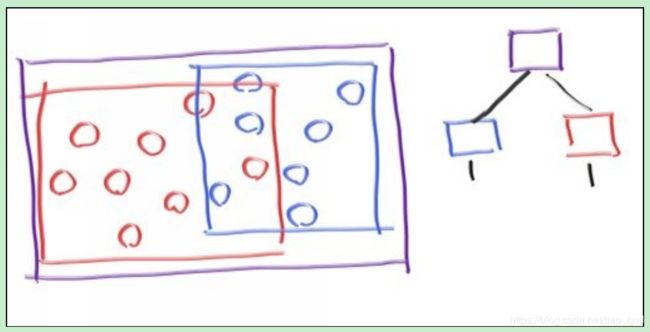
要使事物呈次线性,我们需要使边界体积层次化。例如,如果我们将一组对象分为两组,红色和蓝色,并使用矩形边界体积,我们将得到:
请注意,蓝色和红色的边界卷包含在紫色的边界体中,但它们可能重叠,并且它们没有顺序-它们都在内部。所以右边显示的树没有对左右两个子元素排序的概念;它们只是在里面。代码是:
如果(击中紫色)
hit0=命中蓝色封闭对象
hit1=击中红色封闭对象
如果(hit0或hit1)
返回true和近身命中信息
返回false要使所有这些工作,我们需要一种方法,得到良好的分割而不是不好的分割,以及一种方法,使Ray射线与边界体积相交。光线边界体交点需要快速计算,边界体积需要非常紧凑。在大多数模型的实践中,轴对齐的框比其他替代的效果更好,但是如果遇到不寻常的模型类型,这种设计选择总是需要记住的。
从现在起,我们将称之为轴对齐的边界矩形平行六面体(实际上,如果精确的话,这就是它们需要被称为的)轴对齐的边界框,或AABBs。任何方法,你想使用交叉与AABB射线是好的。我们需要知道的是我们是否击中了它;我们不需要击中点、法线或任何我们想要显示的对象所需要的东西。
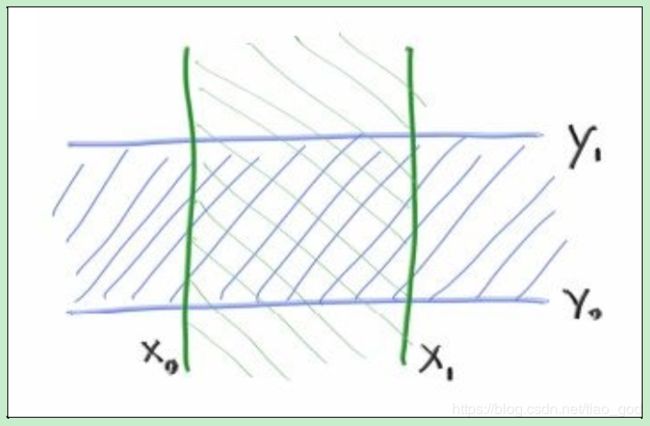
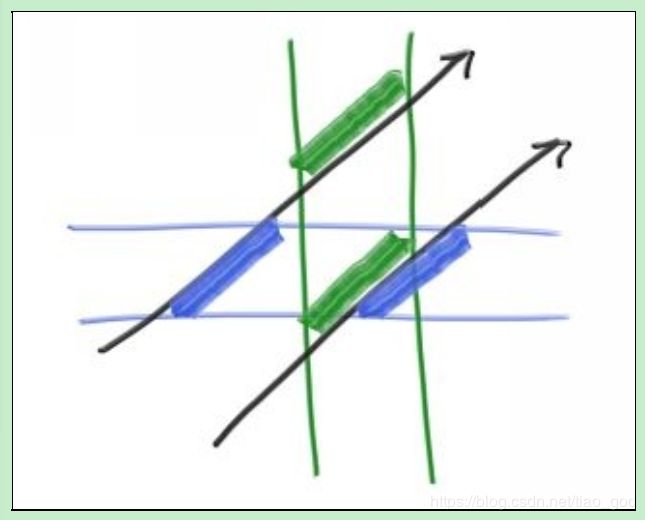
大多数人使用“slab”方法。这是基于一个观察,一个n维AABB只是n轴对齐间隔的交点,通常称为“slab”。间隔只是两个端点之间的点,例如x,使得3 要使光线到达一个间隔,我们首先需要确定光线是否到达边界。例如,同样在2D中,这是光线参数t0和t1。(如果光线与平面平行,则这些将是未定义的。) 在3D中,这些边界是平面。平面的方程是x=x0和x=x1。射线在哪里击中哪个平面?回想一下,光线可以被看作是一个给定t返回位置p(t)的函数: p(t) = A + tB x0 = Ax + t0* Bx t0 = (x0 - Ax) / Bx 将一维数学转化为命中测试的关键观察是,对于命中,t间隔需要重叠。例如,在2D中,绿色和蓝色重叠仅在命中时发生: 什么“板中的t间隔重叠?“代码中的“希望”类似于: 这是非常简单的,事实上,3D版本也可以工作,这就是人们喜欢slab方法的原因: 有一些注意事项使它比最初看起来更不漂亮。首先,假设射线在负x方向运动。上面计算的间隔(tx0,tx1)可能是相反的,例如(7,3)。第二,这里的分界可以给我们无穷大。如果光线的原点在一个平板边界上,我们可以得到一个NaN(非正常数据)。在各种光线跟踪器的AABB中,有许多方法可以处理这些问题(还有一些矢量化问题,如SIMD,我们将不在这里讨论)。如果你想在速度矢量化方面多学习一些内容的话,英戈·沃尔德的论文是一个很好的起点。)就我们的目的而言,只要我们把它做得相当快,这就不太可能成为一个主要的瓶颈,所以让我们去做最简单的,这通常是最快的!首先让我们看一下计算间隔: 一个麻烦的事情是完全有效的ray将有Bx=0,导致除以0。其中一些射线在板内,而另一些则不在板内。此外,在IEEE浮点下,零将有一个正负号。Bx=0的好消息是,如果不是在x0和x1之间,tx0和tx1都是+infty或都是-infty。所以,使用min和max应该能得到正确的答案: 如果我们这样做,剩下的麻烦是如果Bx=0,x0-Ax=0或x1-Ax=0,那么我们得到一个NaN。在这种情况下,我们可能会接受击中或没有击中的答案,但我们将稍后再讨论。 现在,让我们看看重叠函数。假设我们可以假设间隔没有反转(因此第一个值小于间隔中的第二个值),并且我们希望在这种情况下返回true。计算区间(d,d)和(e,e)的重叠区间(f,f)的布尔重叠为: 如果有任何NaN在那里运行,比较将返回false,因此我们需要确保我们的边界框有一点填充,如果我们关心擦边的情况(我们可能应该去关心,因为在光线跟踪器中所有情况最终都会出现)。当所有三维空间都在一个循环中,并在间隔tmin,tmax中传递时,我们得到: 注意,内置的fmax()被ffmax()替换,因为它不担心NaNs和其他异常,所以速度要快得多。在回顾这种交集方法时,Pixar的Andrew Kensler做了一些实验,提出了这个版本的代码,它在许多编译器上都非常有效,我把它作为我的入门方法: 我们现在需要添加一个函数来计算所有hitable的边界框。然后我们将在所有基本体上建立一个框的层次结构,各个基本体(如球体)将在叶子上。该函数返回布尔值,因为并非所有元素都有边界框(例如无限平面)。此外,对象会移动,因此帧的间隔需要时间1和时间2,并且边界框将绑定通过该间隔移动的对象。 对于移动的球体,我们可以取t0处的球体的长方体,t1处的球体的长方体,然后计算这两个长方体的长方体: BVH也将是一个hitable-就像list上的hitable。它实际上是一个容器,但它可以响应“this ray hit you?”. 一个设计问题是我们是否有两个类,一个用于树,一个用于树中的节点;或者我们是否只有一个类,并且根只是我们指向的节点。如果可行的话,我是用一个类设计的爱好者。我们设计这样一个类: 注意,子指针指向的是泛型hitables。它们可以是其他的bvh_notes,或球体,或任何其他hitable。 hit函数非常简单:检查节点的框是否被击中,如果是,则检查子节点并整理任何详细信息: 任何效率结构中最复杂的部分,包括BVH,都是在建造它。我们在构造函数中这样做。bvh的一个很酷的地方是,只要bvh_节点中的对象列表被分成两个子列表,hit函数就可以工作。如果分割做得好,这样两个子对象的边界框比父对象的边界框小,效果最好,但这是为了速度而不是正确性。我将选择中间位置,并在每个节点沿一个轴拆分列表。我要简单一点: 1) 随机选择轴 2) 使用库qsort对元素排序 3) 每子树放一半 我使用旧的C排序qsort,而不是C++排序sort,因为我需要一个不同的比较运算符取决于轴,q排序采取比较函数,而不是使用less-than运算符。我传入一个指向指针的指针-这只是“指针数组”的C,因为C中的指针也可以只是指向数组第一个元素的指针。当传入的列表是两个元素时,我在每个子树中放入一个元素并结束递归。 遍历算法应该是平滑的,不必检查空指针,所以如果我只有一个元素,我会在每个子树中复制它。显式地检查三个元素并遵循一个递归可能会有点帮助,但我想整个方法稍后会得到优化。这将产生: 检查是否有一个边界框是为了以防您发送的内容类似于一个没有边界框的无限平面。我们没有这些元素,所以在添加这些元素之前我们不需要进行检查。那个compare函数必须接受您所转换的空指针。这是老的C函数,提醒我为什么C++被发明了。我把这个搞的真的很乱了,才把所有的指针都弄好。如果你喜欢这部分,你未来将会成为一个能够实现系统的人! 写好以后,下一节我们来测试一下。
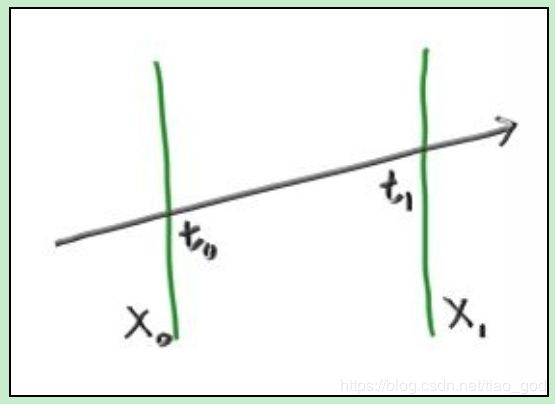
这个方程适用于所有三个x/y/z坐标。例如x(t)=Ax+t*Bx。射线在满足以下等式的t处撞击平面x=x0:
因此 t 在撞击点是:
我们得到了x1的类似表达式t1=(x1-Ax)/Bx。compute (tx0, tx1)
compute (ty0, ty1)
return overlap?( (tx0, tx1), (ty0, ty1))compute (tx0, tx1)
compute (ty0, ty1)
compute (tz0, tz1)
return overlap?( (tx0, tx1), (ty0, ty1), (tz0, tz1))tx0 = (x0 - Ax) / Bx
tx1 = (x1 - Ax) / Bxtx0 = min((x0 - Ax) / Bx, (x1 - Ax) / Bx);
tx1 = max((x0 - Ax) / Bx, (x1 - Ax) / Bx);bool overlap(d, D, e, E, f, F)
f = max(d, e)
F = min(D, E)
return (f < F)#ifndef __AABB_H__
#define __AABB_H__
#include "vec3.h"
#include "ray.h"
inline float ffmin(float a, float b) { return a < b ? a : b; }
inline float ffmax(float a, float b) { return a > b ? a : b; }
class aabb {
public:
aabb(){}
aabb(const vec3&a, const vec3&b) { _min = a;_max = b; }
vec3 min()const { return _min; }
vec3 max()const { return _max; }
bool hit(const ray& r,float tmin,float tmax)const {
for (int a = 0;a < 3;a++) {
float t0 = ffmin((_min[a]-r.origin()[a])/r.direction()[a],
(_max[a]-r.origin()[a])/r.direction()[a]);
float t1 = ffmax((_min[a]-r.origin()[a])/r.direction()[a],
(_max[a] - r.origin()[a]) / r.direction()[a]);
tmin = ffmax(t0, tmin);
tmax = ffmin(t1, tmax);
if (tmax <= tmin)return false;
}
}
vec3 _min;
vec3 _max;
};
#endifbool sphere::bounding_box(float t0, float t1, aabb& box)const {
box = aabb(center - vec3(radius, radius, radius), center + vec3(radius, radius, radius));
return true;
}aabb surrounding_box(aabb box0, aabb box1) {
vec3 small(fmin(box0.rmin().x(),box1.rmin().x()),
fmin(box0.rmin().y(),box1.rmin().y()),
fmin(box0.rmin().z(), box1.rmin().z()));
vec3 big(fmax(box0.rmax().x(), box1.rmax().x()),
fmax(box0.rmax().y(), box1.rmax().y()),
fmax(box0.rmax().z(), box1.rmax().z()));
}
bool moving_sphere::bounding_box(float t0, float t1, aabb&box)const {
vec3 v_radius(radius, radius, radius);
box = surrounding_box(aabb(center0-v_radius,center0+v_radius),aabb(center1 - v_radius, center1 + v_radius));
return true;
}class bvh_node :public hitable {
public:
bvh_node() {}
bvh_node(hitable **l, int n, float time0,float time1);
virtual bool hit(const ray&r, float t_min, float t_max, hit_record&rec)const;
virtual bool bounding_box(float t0, float t1, aabb&box)const;
hitable *left;
hitable *right;
aabb box;
};
bool bvh_node::bounding_box(float t0, float t1, aabb& b)const {
b = box;
return true;
}bool bvh_node::hit(const ray&r, float t_min, float t_max, hit_record &rec)const {
if (box.hit(r, t_min, t_max)) {
hit_record left_rec, right_rec;
bool hit_left = left->hit(r, t_min, t_max, left_rec);
bool hit_right = right->hit(r, t_min, t_max, right_rec);
if (hit_left && hit_right) {
if (left_rec.t < right_rec.t)
rec = left_rec;
else
rec = right_rec;
return true;
}
else if (hit_left) {
rec = left_rec;
return true;
}
else if (hit_right) {
rec = right_rec;
return true;
}
else
return false;
}
else return false;
}
bvh_node::bvh_node(hitable **l, int n, float time0, float time1) {
int axis = int(3 * myRandom());
if (axis == 0)
qsort(l, n, sizeof(hitable*), box_x_compare);
else if (axis == 1)
qsort(l, n, sizeof(hitable *), box_y_compare);
else
qsort(l, n, sizeof(hitable *), box_z_compare);
if (n == 1) {
left = right = l[0];
}
else if (n == 2) {
left = l[0];
right = l[1];
}
else {
left = new bvh_node(l,n/2,time0,time1);
right = new bvh_node(l+n/2,n-n/2,time0,time1);
}
aabb box_left, box_right;
if (!left->bounding_box(time0, time1, box_left) || !right->bounding_box(time0, time1, box_right));
box = surrounding_box(box_left, box_right);
}int box_x_compare(const void *a, const void *b) {
aabb box_left, box_right;
hitable *ah = *(hitable**)a;
hitable *bh = *(hitable**)b;
if (!ah->bounding_box(0, 0, box_left) || !bh->bounding_box(0, 0, box_right))
return 0;//输出错误信息
if (box_left.rmin().x() - box_right.rmin().x() < 0.0)return -1;
else return 1;
}
int box_y_compare(const void *a, const void *b) {
aabb box_left, box_right;
hitable *ah = *(hitable**)a;
hitable *bh = *(hitable**)b;
//if (!ah->bounding_box(0, 0, box_left) || !bh->bounding_box(0, 0, box_right))
// return 0;//输出错误信息
if (box_left.rmin().y() - box_right.rmin().y() < 0.0)return -1;
else return 1;
}
int box_z_compare(const void *a, const void *b) {
aabb box_left, box_right;
hitable *ah = *(hitable**)a;
hitable *bh = *(hitable**)b;
//if (!ah->bounding_box(0, 0, box_left) || !bh->bounding_box(0, 0, box_right))
// return 0;//输出错误信息
if (box_left.rmin().z() - box_right.rmin().z() < 0.0)return -1;
else return 1;
}