机器学习---降维之PCA主成分分析法
(一)、主成分分析法PCA简介
- PCA 目的:降维——find a low dimension surface on which to project data ~
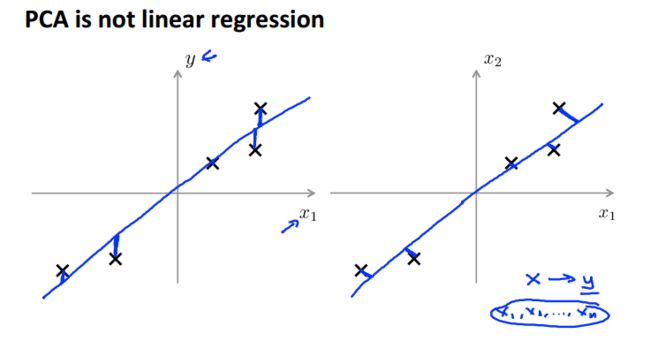
如图所示,寻找蓝色的点到直线的垂直距离的和最小的直线(向量)
PCA 与 Linear Regression 的区别:
PCA衡量的是点到直线的垂直距离, 而linear regression是所有x点对应的真实值y=g(x)与估计值f(x)之间的vertical distance距离,如下图所示:
(二)、PCA 算法流程
第二步:PCA算法选取k个主分量
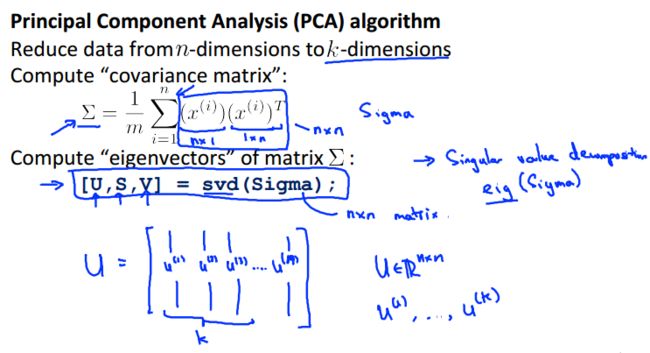
1. 求n×n的协方差矩阵Σ:
2. 根据SVD求取特征值和特征向量:
[U,S,V] = SVD(Σ)
其中,SVD为奇异值分解(singular value decomposition),在matlab中有函数[U,S,V] = svd(A) 返回一个与A同大小的对角矩阵S(由Σ的特征值组成),两个酉矩阵U和V,且满足= U*S*V'。若A为m×n阵,则U为m×m阵,V为n×n阵。奇异值在S的对角线上,非负且按降序排列。
那么对于方阵Σ呢,就有
Σ = USV'
ΣΣ' = USV'*VS'U' = U(ΣΣ')U'
Σ'Σ = VS'U'*USV' = V(Σ'Σ)V'
i.e. U是ΣΣ'的特征向量矩阵;V是Σ'Σ的特征向量矩阵,都是n*n的矩阵
由于方阵的SVD相当于特征值分解,所以事实上U = V, 即Σ = USU', U是特征向量组成的正交矩阵(数值分析这门课中关于矩阵分解有相关介绍)
我们的目的是,从n维降维到k维,也就是选出这n个特征中最重要的k个,也就是选出特征值最大的k个~so...goto next step
3. 按特征值从大到小排列,重新组织U
如果使用matlab的svd求得特征值,就可以直接跳过这步了,因为该函数返回值中,奇异值在S的对角线上按照降序排列。否则的话应进行排序,并按照该次序找到对应的特征向量重新排列。
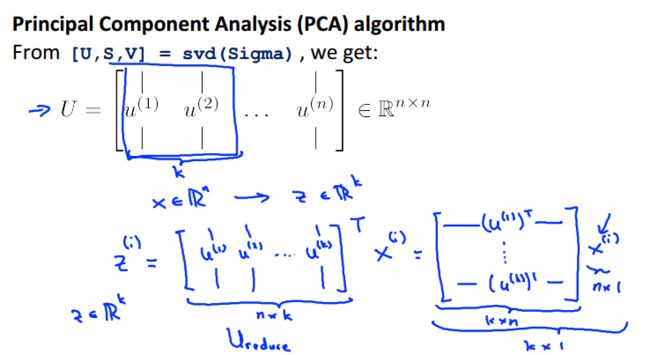
4. 选择k个分量
按照第五、六步中讲的svd过后,我们得到了一个n×n的矩阵Σ和U,这时,我们就需要从U中选出k个最重要的分量;即选择前k个特征向量,即为Ureduce, 该矩阵大小为n×k
这样对于一个n维向量x,就可以降维到k维向量z了:
=====================================
(三)、从压缩数据中恢复原数据
由于Ureduce是正交矩阵(下面Ureduce简记为U),即U' = U-1, 所以
xapprox = (U')-1×z = (U-1)-1×z = Uz
(PS:这里的逆操作为伪逆操作)
注意:这里恢复出的xapprox并不是原先的x,而是向量x的近似值。(恢复后相当于将2D到1D时,将投影作为原先的点)
=====================================
(四)、怎样决定降维个数/主成分个数
首先从一个general一点的思路去想呢,我们是希望,选出主成分之后进行数据分析,不会造成大量特征的丢失,也就是说可以用下式的error ratio表示经过压缩后的性能如何。
error ratio =
然后呢,我们定义一个threshold(10% for example),如果error ratio
从数学上可以证明,上面这个error ratio 可以表示为
所以,可以用下式进行k的合理选取:
(五)、应用PCA进行降维的建议
Ans:NO!应用PCA提取主成分可能会解决一些overfitting的问题,但是呢,不建议用这种方法解决overfitting问题,还是建议用第三章中讲过的加入regularization项(也称为ridge regression)来解决。毕竟,PCA降维过程中是丢弃了某些特征,存在数据损失。
2. PCA中主成分分析应用到那部分数据呢?
Ans:Only Training Data!可以用Cross-Validation data 和 test Data进行检验,但是选择主分量的时候只应用training data.
3. 不要盲目PCA
Notice:只有当你在源数据上处理结果不理想时,可以考虑用PCA处理。
参考:http://blog.csdn.net/abcjennifer/article/details/8002329