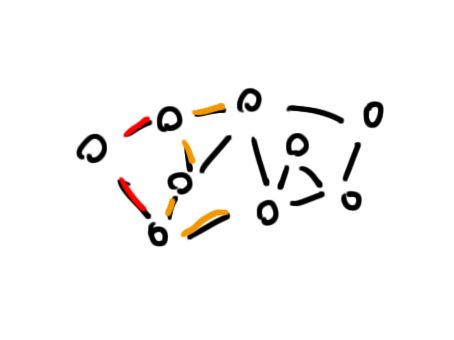深入理解Bellman-Ford(SPFA)算法
前言
Bellman-Ford算法,限于资料匮乏和时间复杂度比Dijkstra算法高,包括白书在内的很多资料,都没说得太明白。对于优化后的SPFA算法也没有提及。
而且最短路问题通常是作为图论的入门问题,学习者通常没有图论基础,不知道图论的一些基本常识,看已有的资料很容易产生疑惑。其实,从Bellman-ford算法优化到SPFA算法实际上是顺理成章的。
本文旨在阐明这两个算法思想和步骤,如果有什么晦涩或者疏漏之处在所难免,烦劳读者们指出。
这里是我的个人网站:
https://endlesslethe.com/bellmanford-spfa-tutorial.html
有更多总结分享,最新更新也只会发布在我的个人网站上。
排版也可能会更好看一点=v=
Bellman-Ford算法有什么用
Bellman-Ford算法是用来解决单源最短路问题的。
在现实生活旅游途中,我们通常想知道一个景点到其他所有景点的最短距离,以方便我们决定去哪些比较近的景点。而这时候,Bellman-Ford算法就有用了。
Bellman-Ford算法的优点是可以发现负圈,缺点是时间复杂度比Dijkstra算法高。
而SPFA算法是使用队列优化的Bellman-Ford版本,其在时间复杂度和编程难度上都比其他算法有优势。
算法流程
(1)初始化:将除起点s外所有顶点的距离数组置无穷大 d[v] = INF, d[s] = 0
(2)迭代:遍历图中的每条边,对边的两个顶点分别进行一次松弛操作,直到没有点能被再次松弛
(3)判断负圈:如果迭代超过V-1次,则存在负圈
我们用距离数组d[i]来记录起点s到点i的最短距离。
看了上面的算法流程,通常我们会有四个问题:
- 什么是松弛操作
- 迭代多少次?
- 迭代的实际意义是什么?
- 为什么迭代超过v-1次就存在负圈?
直观理解松弛操作

如图,假设选取边<3,4>来进行松弛操作,那么进行两次如下操作(w为边权):
d[3] = min(d[3], d[4]+w) // 对点3
d[4] = min(d[4], d[3]+w) // 对点4
这样做的目的是让距离数组d尽量的小。
而每一次让d[i]减小的松弛操作,我们都称其“松弛成功”。
而实际中,我们使用的松弛操作可以是选取一条边,也可以是从一个点from到另一个点to。后者对应的松弛操作为:
d[to] = min(d[to], d[from] + w)
从最短路的角度来讲,如果对点3的松弛操作成功,意味着从s到4再从4到3这条路比其他从s到3的路都短,距离数组中的d[3]就是目前起点到点3的最短距离。
我们可以总结为:每一次成功的松弛操作,都意味着我们发现了一条新的最短路。
直观理解迭代
第二第三个问题实际上都是同一个问题:迭代的实际意义是什么?
这里我先给出迭代的定义:每次都遍历图中的所有边,对每条边(的两个端点)都进行松弛操作。
下面,我们以上图中的点和边为例,讲清楚迭代的实际意义:
第一次迭代
第二次迭代
从这次迭代中,我们可以发现一个定理:只有上一次迭代中松弛过的点才有可能参与下一次迭代的松弛操作。
这里的“参与”指让邻点距离数组d[i]改变。
这个定理很容易理解,如果两个点的距离数组d[i]在上一次迭代后没有改变,那么这次也不会改变。只有上一次改变了的点才会影响周围的点。
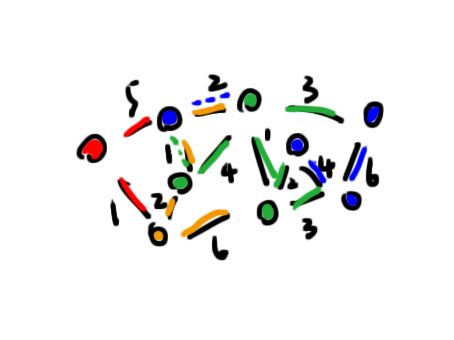
第三次迭代
这次的示意图比上两次都要复杂许多,我给每条边都标注上了权值,不同迭代中改变过值的点也用不同颜色标注了出来。每条松弛过的边我也标注了出来。

我们重点注意边<3,4>中的点3被松弛了,图中标注为一条虚线。
回忆一下前面的内容,这意味着,我们发现了点3新的最短路,这个最短路经历了3条边。
这里揭示了迭代的实际意义:每次迭代k,我们找到了经历了k条边的最短路。
值得注意的是,在迭代还没结束时的最短路不一定是最终的最短路。有可能最终的最短路经历的边很多,但每条边的权值很小,比经历边少的路线距离更短。
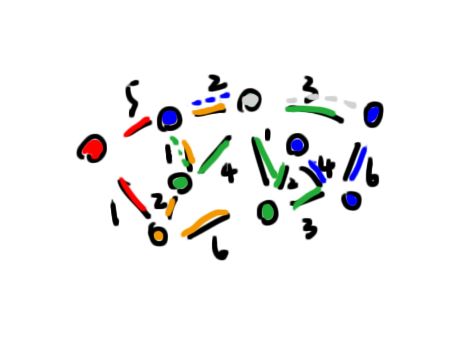
第四次迭代
第五次迭代
第六次迭代
注意到没有点能够被松弛,根据之前发现的定理“只有上一次迭代中松弛过的点才有可能参与下一次迭代的松弛操作”,因为不再存在能够被松弛的点了,迭代结束。
总结
- 定理一:只有上一次迭代中松弛过的点才有可能参与下一次迭代的松弛操作
- 迭代的实际意义:每次迭代k中,我们找到了经历了k条边的最短路。
- “没有点能够被松弛”时,迭代结束
根据定理一“只有上一次迭代中松弛过的点才有可能参与下一次迭代的松弛操作”,似乎算法中遍历每条边的做法比较菜,我们只需要考虑那些被成功松弛的点的邻点不就好了吗?答案是肯定的。我们可以简单地通过一个队列来维护这些被成功松弛的点,这个小小的改进可以带来巨大加速,改进之后的算法被称为SPFA。
直观理解负圈
符合常识地,有定理二:如果在边权都为正的图中,最短路一定是一条路径,而不是一个圈,且长度不会大于等于V
拓展到存在负边权的图中,有定理三:对于存在负圈的图,最短路无意义
定理四:对于不存在负圈的图,最短路一定是一条路径,且长度不会大于等于V

如图所示,因为有边长为1、-2、-1的负圈存在,起点到其余所有点的距离都是-INF,因为到其余所有点的路上都可以经过这个负圈无穷次,这时候最短路没有意义。
对于Bellman-Ford算法,因为一个最短路如果不存在负圈的话,不会经历超过V-1条边,所以假如迭代次数大于等于V,就存在负圈。
Note:网上很多代码没有理解每次迭代的意义,采用每个节点的入队次数来判断负圈,当然也是可以,但是大大增加了运行时间。
写在最后
在SPFA的基础上,我们或许还能进行一些优化,比如参考文献表中的SLF和LLL,这里我就不多提了,有兴趣可以看一下,就一两行代码的事。
希望大家看完本文能够完全理解SPFA。
Bellman-ford实现代码
因为这道题点比较少,就使用了邻接矩阵来储存图。实际上,用得比较多的储存方法是邻接表和前向星,有兴趣了解的戳——“浅谈图的组织(邻接表、前向星)”【TBC】
/**
* @Date: 28-Jun-2018
* @Email: [email protected]
* @Filename: POJ 3259【bellman-ford】.cpp
@Last modified time: 04-Jul-2018
* @Copyright: ©2018 EndlessLethe. All rights reserved.
*/
#pragma comment(linker, "/STACK:102400000,102400000")
#include
#include
#include
#include
using namespace std;
const int MAXN = 500+10;
int G[MAXN][MAXN];
int d[MAXN];
int vis[MAXN];
bool bellman_ford(int s, int N) {
int flag;
for (int i = 0; i < N; i++) {
flag = 0;//如果不能松弛,则停止
for (int j = 0; j < N; j++) {
for (int k = 0; k < N; k++) {
if (d[k] > d[j] + G[j][k]) {
d[k] = d[j] + G[j][k];
flag = 1;
}
}
}
if (!flag) return 1;//不存在负环
}
flag = 0;
for (int j = 0; j < N; j++) {
for (int k = 0; k < N; k++) {
if (d[k] > d[j] + G[j][k]) {
flag = 1;
}
}
}
return !flag;
}
int main() {
int F, N, M, W, S, E, T;
cin >> F;
while (F--) {
memset(G, 0x3f, sizeof(G));
memset(d, 0x3f, sizeof(d));
memset(vis, 0, sizeof(vis));
cin >> N >> M >> W;
for (int i = 0; i < M; i++) {
cin >> S >> E >> T;
S--, E--;
if (T < G[S][E]) G[S][E] = G[E][S] = T;
}
for (int i = 0; i < W; i++) {
cin >> S >> E >> T;
S--, E--;
G[S][E] = -T;
}
if (bellman_ford(0, N)) cout << "NO" << endl;
else cout << "YES" << endl;
}
return 0;
}
SPFA实现代码
/**
* @Date: 28-Jun-2018
* @Email: [email protected]
* @Filename: POJ 3259【bellman-ford】.cpp
@Last modified time: 04-Jul-2018
* @Copyright: ©2018 EndlessLethe. All rights reserved.
*/
#pragma comment(linker, "/STACK:102400000,102400000")
#include
#include
#include
#include
#include
#include
using namespace std;
const int MAXN = 500+10;
int G[MAXN][MAXN];
int d[MAXN];
int vis[MAXN];
queue q;
bool bellman_ford(int s, int N) {
d[s] = 0;
int cnt = 0;
q.push(s);
q.push(cnt);
vis[s] = 1;
while (!q.empty()) {
int x = q.front(); q.pop();
cnt = q.front(); q.pop();
vis[x] = 0;
if (cnt > N) return 0;
for (int i = 0; i < N; i++) {
if (d[i] > d[x] + G[x][i]) {
d[i] = d[x] + G[x][i];
if (!vis[i]) {
q.push(i);
q.push(cnt+1);
vis[i] = 1;
}
}
}
}
return 1;
}
int main() {
int F, N, M, W, S, E, T;
cin >> F;
while (F--) {
while (!q.empty()) q.pop();
memset(G, 0x3f, sizeof(G));
memset(d, 0x3f, sizeof(d));
memset(vis, 0, sizeof(vis));
cin >> N >> M >> W;
for (int i = 0; i < M; i++) {
cin >> S >> E >> T;
S--, E--;
if (T < G[S][E]) G[S][E] = G[E][S] = T;
}
for (int i = 0; i < W; i++) {
cin >> S >> E >> T;
S--, E--;
G[S][E] = -T;
}
if (bellman_ford(0, N)) cout << "NO" << endl;
else cout << "YES" << endl;
}
return 0;
}
题目总结
- POJ 3259
有重边,使用邻接矩阵要注意。算法本身不在乎重边的情况,使用邻接表的话,对于虫洞直接添加一条新的边即可 - POJ 1860
参考文献
I. 《挑战程序设计竞赛》
II. Bellman-Ford 算法及其优化
III. 最短路径算法—Bellman-Ford(贝尔曼-福特)算法分析与实现(C/C++)
IV. SPFA的两种优化SLF和LLL
V. 请柬(双向SPFA及SLF LLL优化法模板题)