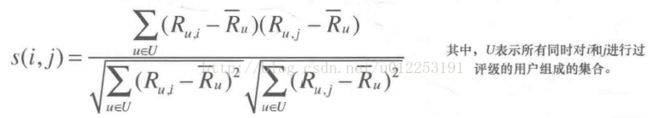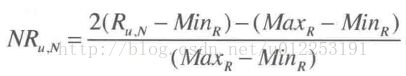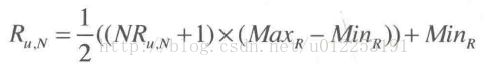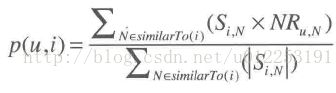数据挖掘python学习——《写给程序员的数据挖掘实践指南》第3章

第3章  协同过滤——隐式评级及基于物品的过滤

对于一些5分区间，10分区间等的评分机智，用户的评分方式可能倾向于极端化，集中在高分或是集中在低分，这样参差不平的评分对于结果的准确性产生较大的影响。这一章考察对协同过滤的调优方法，目的是高效地产生更精准的预测结果。

讨论了显式评级和隐式评级：

显示评级：用户直接评级。

问题1：用户大都具有惰性，不愿意对物品评级；

问题2：用户可能撒谎或者只给出部分信息；

问题3：用户不会更新其评级结果。

隐式评级：不需要用户给出任何评级得分，而是观察用户的行为来获得结果。

问题：可能由于多用户共用账号或是多目的行为使得预测不准确。

基于用户的过滤（也叫基于内存的协同过滤——memory based collaborative filtering）：

此前的考虑都是找寻最近的比配用户，这种做法在有些情况下存在以下两种问题：

1. 扩展性。现实生活中，用户的数量级往往不止成百上千。一旦用户的数量过于庞大，其扩展性存在一定问题；

2. 稀疏性。在大部分推荐系统中，用户和商品都很多，但是用户评级的平均商品数目却很小，可能找不到最近邻居。

我们在进行数据挖掘的时候，需要针对不同的数据的意义和数量调整预测方案。

为解决以上问题，提出基于物品的过滤——Item-based Filtering（也叫基于模型的协同过滤——model based collaborative filtering）。与基于内存的方法相比，基于模型的方法扩展性更好。对于大型数据集，这种方法更快，需要的内存更少。

分数贬值（分数夸大）现象：分数很高，超过实际应得的分数。

为抵消这种状况，从每个评级结果中减去平均的评级结果，以下为对余弦相似度的调整。

做归一化处理。求得用户对所有物品评分的平均值，每次计算将该物品的评分减去平均值。余弦相似度计算公式经过处理后如下：

依照上述公式实现函数如下：

from math import sqrt

def computeSimilarity (band1, band2, users):
    averages = {}
    for (key, ratings) in users.items():
        averages[key] = (float(sum(ratings.values())))/len(ratings.values())

    sum1 = 0
    sum2 = 0
    sum3 = 0

    for (user, ratings) in users.items():
        if band1 in ratings and band2 in ratings:
            avg = averages[user]
            sum1 += (ratings[band1] - avg) * (ratings[band2] - avg)
            sum2 += (ratings[band1] - avg) ** 2
            sum3 += (ratings[band2] - avg) ** 2

    sum23 = sqrt(sum2) * sqrt(sum3)
    if sum != 0:
        return sum1/sum23
    else:
        return 0

users = {"David": {"Imagine Dragons": 3, "Daft Punk": 5,
                    "Lorde": 4, "Fall Out Boy": 1},
          "Matt":  {"Imagine Dragons": 3, "Daft Punk": 4,
                    "Lorde": 4, "Fall Out Boy": 1},
          "Ben":   {"Kacey Musgraves": 4, "Imagine Dragons": 3,
                    "Lorde": 3, "Fall Out Boy": 1},
          "Chris": {"Kacey Musgraves": 4, "Imagine Dragons": 4,
                    "Daft Punk": 4, "Lorde": 3, "Fall Out Boy": 1},
          "Tori":  {"Kacey Musgraves": 5, "Imagine Dragons": 4,
                    "Daft Punk": 5, "Fall Out Boy": 3}}

print(computeSimilarity('Lorde', 'Kacey Musgraves', users))

输出结果如下：

基于以上的内容，我们可以利用余弦相似度的计算公式计算两个物品间的相似度进行预测。

为了预测公式能够以最佳的方式进行，需要将用户的评分结果先转换为-1到1之间的数值，计算得到结果之后再转换为1到5的评级。

用户评分结果归一化公式如下：

复原公式如下：

预测公式如下：

【Slope One 算法】

也是基于物品过滤的算法。利用物品对的偏差进行预测。

主要优点：简洁性，容易实现。

第一步：

第二步：