趣谈递归算法

　　记得之前小罗师傅给我写过一个有趣的VBS程序，代码就不说了，它讲的是一个有趣的小故事：“山上有座庙，庙里有个老和尚很爱跟人家讲故事，故事是这样的：山上有座庙，庙里有个老和尚很爱跟人家讲故事，故事是这样的...”你一定凌乱了：这老和尚是什么鬼！！总是一直重复自己说的话呢？？？

[自拍也是递归哟]

一、什么是递归调用

　　哈哈，一个小玩笑，引出递归的定义，程序调用自身的编程技巧就是递归。当然不是无限的死循环啦！！看了本Java的书，发现在三大控制结构这章，多了一节递归。开始还在想，为什么作者要这样编写这本书，敲了一个小例子跟“当循环”一对比才发现啊，递归是一种特殊的循环。

二、递归的基本思想

　　递归被发明出来是解决什么问题的呢？当需要解决一个很复杂的问题的时候，需要我们把这个大的问题化解为类似的几个小问题，直到问题简单到可以直接求解。其中需要注意的是，要有两点条件需要满足才能形成递归：

一是，保证函数中需要调用到自身；

二是，要有一个递归出口，即当满足一定条件的时候，有一个明确的结束。（return）

作用：少量的程序去解决重复的计算，大大减少了代码量。

三、例子分析（递归就是循环）

　　先来说一个Fibonacci函数（数列从第三项开始，每个都是前两个的和）：1,1,2,3,5,8.......

public class Test2{
		public static void main(String arg[]){
				System.out.println(f(5));
			}
		public static int f(int n){
				if(n==1||n==2){
						return 1;
					}
				else {
						return f(n-1)+f(n-2);
					}
			}
	}

结果：

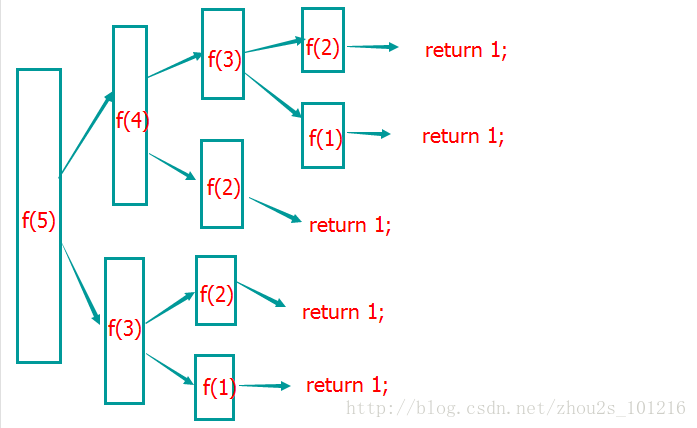
递归过程：

　　看到了上面的图，是不是很容易就理解了5是怎么得来的。这样如果问你复杂的100,1000,10000通过一个F()，也可以很容易推算出来了。看到上面的代码获取你会发现IF 下的语句就是递归出口，当满足括号中的条件时就可以跳出递归，否则（ELSE）就一直执行自己。这里括号中的作用就是While的作用。所以，我觉得可以把递归看出一种特殊的循环。

四、汉诺塔下的递归算法

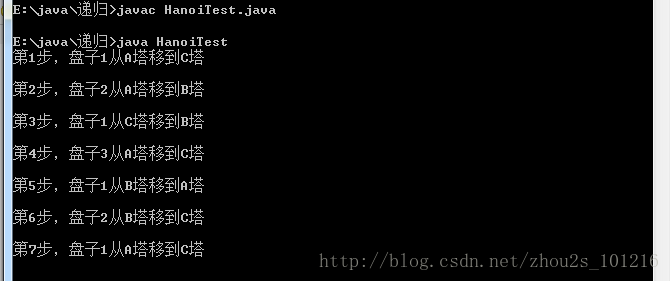
　　不知道大家有没有玩过下面这个游戏。有三根柱子a，b，c（从左向右依次命名），a柱子上有3个盘子，从小到大依次叠放，要求把a上的盘子都移到c上，b可以作为临时存放，移动的时候必须始终遵循小盘子在大盘子上面，且所有的塔只能从下而上依次变小，小盘子不能罗在大的下面。这就是经典的汉诺塔游戏。

代码实现：

public class HanoiTest {

	static int step = 0;
	/**
	 * @param args
	 */
	public static void main(String[] args) {
		hanioSort(3, "A", "B", "C");
	}
	
	/**
	 * 递归函数，用来遍历hanoi步骤
	 *@param num 是盘子的编号，第1,2,3个盘子
	 *@param a\b\c是塔名，指A,B,C塔
	 
	 
	 */
	public static void hanioSort(int num ,String a ,String b ,String c){
		if(num == 1){
			move(num,a,c);
		} else{
			hanioSort(num-1, a, c, b);
			move(num,a,c);
			hanioSort(num-1, b, a, c);
		}
	}
	public static void move(int num ,String a,String b){
		step ++ ;
		System.out.println("第"+step+"步，盘子"+num+"从"+a+"塔移到"+b+"塔\n");
	}
}

结果：

五、小结

　　通过上面的例子相信你对递归也有一定的了解了，其实在VB学习的时候就用循环实现过Fibonacci函数的例子，在C++学习的时候也学过汉诺塔的例子。当时没有搞懂，只是停留在看的阶段，原来是我还没遇到递归算法啊！哈哈。