机器学习-*-DBSCAN聚类及代码实现
DBSCAN
DBSCAN(Density-Based Spatial Clustering of Applications with Noise,具有噪声的基于密度的聚类方法)
原理
首先描述以下几个概念,假设我们有数据集 D = { x 1 , x 2 , x 3 , . . . , x n } D=\{x_1,x_2,x_3,...,x_n\} D={x1,x2,x3,...,xn},则
1. ϵ \epsilon ϵ邻域:对于 ∀ x i ∈ D \forall x_i\in D ∀xi∈D,有 N ϵ ( x i ) = { x j ∣ d i s t a n c e ( x i , x j ) < ϵ , 此 处 认 为 i 可 以 等 于 j } N_{\epsilon}(x_i)=\{x_j|distance(x_i,x_j)<\epsilon,此处认为i可以等于j\} Nϵ(xi)={xj∣distance(xi,xj)<ϵ,此处认为i可以等于j},该邻域的数据个数为 C ( N ϵ ( x i ) ) C(N_{\epsilon}(x_i)) C(Nϵ(xi))
2.核心点:设最小邻域内个数为 m i n p t s minpts minpts,若一点 x i x_i xi的 ϵ \epsilon ϵ邻域的 C ( N ϵ ( x i ) ) > = m i n p t s C(N_{\epsilon}(x_i))>=minpts C(Nϵ(xi))>=minpts,则称该点为核心点
3.边界点:若一点 x i x_i xi的 ϵ \epsilon ϵ邻域内 C ( N ϵ ( x i ) ) < m i n p t s C(N_{\epsilon}(x_i))<minpts C(Nϵ(xi))<minpts,且处于核心点邻域内的点,则称该点为边界点
4.噪声点:不是核心点和边界点的其他点为噪声点。
5.密度直达:如果 x i x_i xi在核心点 x j x_j xj的邻域内,则它俩就是密度直达的
6.密度可达:若有核心对象序列 k 1 , k 2 , k 3 , . . . , k m k_1,k_2,k_3,...,k_m k1,k2,k3,...,km,若 k t + 1 k_{t+1} kt+1均可以由 k t k_t kt密度直达,则称 k 1 k_1 k1与 k m k_m km密度可达
密度直达和密度可达是不对称的,不能绝对的反向导出,参见参考文献1
7.密度相连:有点 x i x_i xi x j x_j xj,若他们与核心对象 x k x_k xk密度可达,那么他们俩是密度相连的。这个概念可以对称的。
下边是网上截取的相关示例
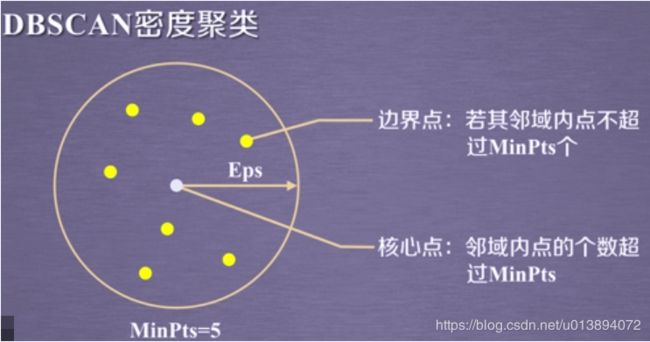
聚类流程
首先阐述一下聚类的思想:以某一核心点为基点,根据密度可达关系、密度相连关系,导出最大样本集类簇,此为第一个类簇;再从剩下的核心点中选取新的为基点重复上述过程;直到所有的核心点被选取完毕,若剩下了样本点,每一个样本点均为一个类别。
具体流程:
1.初始化核心点集合 Ψ \Psi Ψ,遍历数据找到所有的核心点,建立类簇集合 C C C
2.若 Ψ = ∅ \Psi =\emptyset Ψ=∅ 停止迭代 转6,否则 Ψ \Psi Ψ中随机选取一个核心点 o o o(不放回),转3
3.以当前核心点为原点建立一个新的类簇 C o C_o Co,建立当前子样本集 D o D_o Do,子核心点集 Ψ o \Psi_{o} Ψo,将核心点加入 Ψ o \Psi_{o} Ψo和 D o D_o Do
4.遍历 Ψ o \Psi_{o} Ψo,拿取一个核心点(不放回),查询其相关邻域内的点 N ϵ o N_{\epsilon}o Nϵo, N ϵ o N_{\epsilon}o Nϵo中的点加入 D o D_o Do,将 N ϵ o N_{\epsilon}o Nϵo与原始核心点集 Ψ \Psi Ψ做交集,得到的集合再与 Ψ o \Psi_{o} Ψo做并集。
5.不断重复3-4,直到 Ψ o \Psi_{o} Ψo为空,将 D o D_o Do中的点作为类簇 C o C_o Co的成员, C o C_o Co加入 C C C,转2
6.查找余下的未加入到 C C C中的数据,分别单独形成一个类簇加入。
Group的定义及import导入包,请见K均值聚类及代码实现
class Dbscan(object):
"""
dbscan- Density-Based Spatial Clustering of Application with Noise
基于密度的噪声应用空间聚类
"""
def __init__(self,epos=0.1,minpts=5):
self._epos = epos # 邻域半径范围
self._minpts = minpts # 邻域内最小数据个数
self._groups = [] #类簇集合
self._kernel_points = [] #核心对象集合
self._X = {} # 转化后的数据
def _find_nearbours(self,xi,XX):
"""
查找满足邻域值大小的数据索引列表
:param xi:
:param XX:
:return:
"""
if XX.shape[0] == 0:
return []
distances= eculide(xi,XX)
nearst_indexes = np.where(distances <= self._epos)[0].tolist()
return nearst_indexes
def _compat_X(self,X):
"""
转化输入数据格式
为了方便删除、存取操作
:param X:
:return:
"""
rows,_ = X.shape
CX = {}
for row in range(rows):
CX[row]=[False,X[row]]
self._X = CX
def _get_data(self,index):
"""
获取索引的数据
:param index:
:return:
"""
if isinstance(index,int):
data = self._X.get(index)[-1]
if isinstance(index,list):
data = []
for i in index:
data.append(self._X.get(i)[-1])
return data
def _delete_data(self,indexes):
"""
删除索引对应的数据
:param indexes:
:return:
"""
if isinstance(indexes,int):
self._X.get(indexes)[0] = True
if isinstance(indexes, list):
for index in indexes:
self._X.get(index)[0] = True
def _get_live_data(self):
"""
获取未被加入到类簇集合的数据
:return:
"""
live_data = {}
for key,value in self._X.items():
if value[0]==False:
live_data[key] = value
return live_data
def fit(self,X):
"""
聚类主体
:param X:
:return:
"""
self._compat_X(X)#组合X的记录
# 1.首先遍历数据集 找到所有的核心对象
rows,_ = X.shape
for i in range(rows):
# 找到小于邻域参数的数据
nearbours = self._find_nearbours(X[i],X)
if len(nearbours)>=self._minpts:
self._kernel_points.append(i)
if len(self._kernel_points) == 0 :
# 若没有核心对象,那么每个点都为单独的一类
for i in range(rows):
g = Group()
g.name = i+1
g.members = X[i]
g.center = X[i]
self._groups.append(g)
return
while(True):
if len(self._kernel_points) == 0:
break
# 2.4直到当前核心对象集合为空
# 2.从核心对象集合中取出一个核心对象,完成对一个类簇的生成
init_index = int(np.random.randint(0,len(self._kernel_points),size=1).squeeze())
kernel_points = self._kernel_points[init_index]
self._kernel_points.remove(kernel_points)
# 2.1拿取第一个核心对象生成类簇,加入当前核心对象集合
current_points = set() # 当前簇的样本集合
current_kernel_points = set()
g = Group()
g.center = X[kernel_points]
self._delete_data(kernel_points)
current_kernel_points.add(kernel_points)
delete_kernel_points = set()
while len(current_kernel_points)!= 0:
# 2.2然后当前核心对象集合中取一个核心点 找到该核心对象的所有邻域点,则邻域点即为该类簇的成员数据
current_point_index = current_kernel_points.pop()
current_points.add(current_point_index)
delete_kernel_points.add(current_point_index)
nearbours_points_indexes = self._find_nearbours(X[current_point_index],X)
current_points = current_points.union(set(nearbours_points_indexes))
# 2.3用这些成员与原始核心对象集合做交集,若有重合则将其加入当前核心对象集合中,重复上述查询邻域过程
union_kernel_points = current_points.intersection(set(self._kernel_points))
current_kernel_points = current_kernel_points.union(union_kernel_points)
current_kernel_points = current_kernel_points.difference(delete_kernel_points)
# 3 重复上述步骤
current_datas = self._get_data(list(current_points))
self._delete_data(list(current_points))
g.members = current_datas
g.name = len(self._groups) + 1
self._groups.append(g)
s = set(self._kernel_points)
s = s.difference(current_points)
self._kernel_points = list(s)
# 查询现有余下的数据 也就是噪声点
live_datas = self._get_live_data()
for key ,value in live_datas.items():
g = Group()
g.name = len(self._groups) + 1
g.center = value[-1]
g.members = value[-1]
self._groups.append(g)
def plot_example(self):
"""
画图
"""
figure = plt.figure()
ax = figure.add_subplot(111)
ax.set_title("Dbscan Iris Example")
plt.xlabel("first dim")
plt.ylabel("two dim")
legends = []
cxs = []
cys = []
for i in range(len(self._groups)):
group = self._groups[i]
members = group.members
x = [member[0] for member in members]
y = [member[1] for member in members]
cx = group.center[0]
cy = group.center[1]
cxs.append(cx)
cys.append(cy)
ax.scatter(x, y, marker='o')
#ax.scatter(cx,cy,marker='+',c='r')
legends.append(group.name)
plt.scatter(cxs,cys,marker='+',c='k')
plt.legend(legends, loc="best")
plt.show()
def test_dbscan():
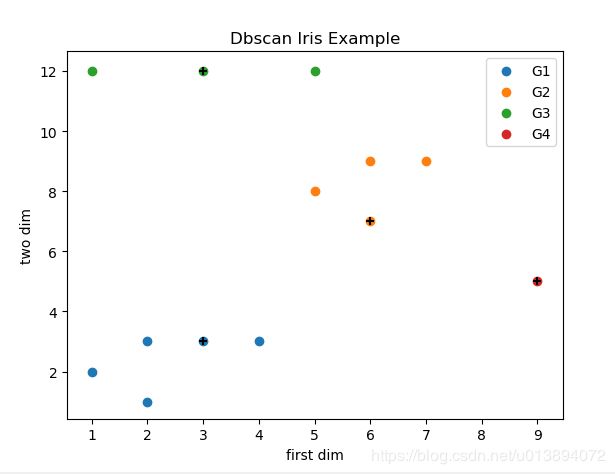
X=np.array([[1,2],[2,1],[2,3],[4,3],[5,8],[6,7],[6,9],[7,9],[9,5],[1,12],[3,12],[5,12],[3,3]])
data,t,tname = load_data()
dbscan = Dbscan(2,3)
dbscan.fit(X)
dbscan.plot_example()
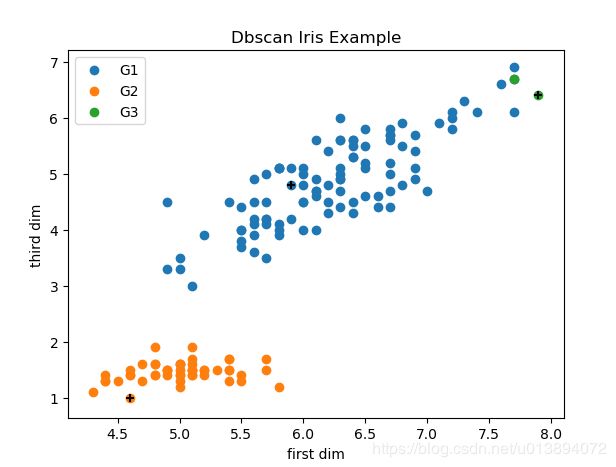
此处分别用了test_dbscan()中的X和data进行实验。
data是iris数据集
总结一下dbscan的特点:
DBSCAN的主要优点有(参考文献1):
1) 可以对任意形状的稠密数据集进行聚类,相对的,K-Means之类的聚类算法一般只适用于凸数据集。
2) 可以在聚类的同时发现异常点,对数据集中的异常点不敏感。
3) 聚类结果没有偏倚,相对的,K-Means之类的聚类算法初始值对聚类结果有很大影响。
DBSCAN的主要缺点有:
1)如果样本集的密度不均匀、聚类间距差相差很大时,聚类质量较差,这时用DBSCAN聚类一般不适合。
2) 如果样本集较大时,聚类收敛时间较长,此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。
3) 调参相对于传统的K-Means之类的聚类算法稍复杂,主要需要对距离阈值ϵ,邻域样本数阈值MinPts联合调参,不同的参数组合对最后的聚类效果有较大影响。
参考文献
1.DBSCAN密度聚类算法
2.无监督学习-DBSCAN聚类算法及应用