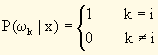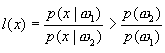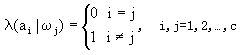贝叶斯(Bayes)决策理论
在博文【模式识别PR和模式的概念】介绍了相关的模式识别与模式的概念。在本节描述所要讨论的问题之前,再提一下对于待识别的物理对象的描述问题。假设一个待识别的物理对象用其d个属性观察值描述,称之为d个特征,这组成一个d维的特征向量,而这d维待征所有可能的取值范围则组成了一个d维的特征空间。
======ps为了说明这句话,我们讨论一个具体的例子======
假设苹果的直径尺寸限定在7厘米到15厘米之间,它们的重量在3两到8两之间变化。如果直径长度x用厘米为单位,重量y以两为单位。那么,由x值从7到15,y值从3到8包围的二维空间就是对苹果进行度量的特征空间。
贝叶斯决策理论方法所讨论的问题是:
已知总共有c类物体,也就是说待识别物体属于这c类中的一个类别,对这c类不同的物理对象,以及各类在这d维特征空间的统计分布,具体说来是各类别ωi=1,2,…,c的先验概率P(ωi)及类条件概率密度函数p(x|ωi)已知的条件下,如何对某一样本按其特征向量分类的问题。由于属于不同类的待识别对象存在着呈现相同观察值的可能,即所观察到的某一样本的特征向量为X,而在c类中又有不止一类可能呈现这一X值,这种可能性可用P(ωi|X)表示。如何作出合理的判决就是贝叶斯决策理论所要讨论的问题。
=================================================
我们知道,一般地,机器实现自动分类有两大类方法:一种是模板匹配方法,另一种是对特征空间划分为子空间(每类的势力范围)的方法。本节是针对第二种方法的。核心问题是:样本为特征向量X时,它属于哪一类可能性有多大,如能确定属于各个类别的百分比(概率)分类决策就有了依据。如:某个样本的特征向量为X,X属于第一类样本的可能性为60%,而第二类的可能性为40%。在没有任何样本信息的情况下,则应将样本决策为第一类以使错分类可能性小(40%),这是本节考虑分类问题的出发点。接下来我们将讨论几种常用的决策规则。不同的决策规则反映了分类器设计者的不同考虑,对决策结果有不同的影响。其中最有代表性的是基于最小错误率的贝叶斯决策与基于最小风险的贝叶斯决策。
基于最小错误率的贝叶斯决策
一般说来,c类不同的物体应该具有各不相同的属性,在d维特征空间,各自有不同的分布。当某一特征向量值X只为某一类物体所特有,即
对其作出决策是容易的,也不会出什么差错。问题在于出现模棱两可的情况。此时,任何决策都存在判错的可能性。这一节讨论的是使错误率为最小的决策方法,称为基于最小错误率的贝叶斯决策理论。最小错误率是在统计的意义上说的,请注意其含义。在这里要弄清楚条件概率这个概念。P(*|#)是条件概率的通用符号,在“|”后边出现的#为条件,之前的*为某个事件,即在某条件#下出现某个事件*的概率。P(ωK|X)是表示在X出现条件下,样本为ωK类的概率。一个事物在某条件下出现的概率P(*|#)与该事件在不带任何条件下出现的概率(写成P(*))是不相同的。例如全世界人口有60亿。因此你见到一个人在不带任何条件下,有20%的可能性是中国人P(*)=0.2,但是如果你在中国,或香港、台湾,那么中国、香港、台湾都是指一种条件(#),这种地理条件下,你所见到的某一个人是中国人(*)的概率就要大得多,此时P(*|#)就应该大于20%,甚至更多了。
在此我们先讨论一个例子:癌细胞的识别,以此说明解决问题的过程。假设每个要识别的细胞已作过预处理,并抽取出了d个特征描述量,用一个d维的特征向量X表示,识别的目的是要依据该X向量将细胞划分为正常细胞或者异常细胞。这里我们用ω1表示是正常细胞,而ω2则属于异常细胞。
类别的状态是一个随机变量,而某种状态出现的概率是可以估计的。概率的估计包含两层含义,一是由统计资料表明,正常细胞与异常细胞在统计意义上的比例,这称为先验概率P(ω1)及P(ω2),另一种则分别表示所检查细胞呈现出不同属性的概率密度函数P(x|ω1)和P(x|ω2),显然在一般情况下正常细胞占比例大,即P(ω1)>P(ω2),因此如果我们不对具体的细胞化验值作仔细观察,我们作出该细胞是正常细胞的判决,在统计的意义上来说,也就是平均意义上说,错判可能性比判为异常细胞时小。但是仅按先验概率来决策,就会把所有细胞都划归为正常细胞,并没有达到将正常细胞与异常细胞区分开的目的。这表明由先验概率所提供的信息太少。
为此我们还必须利用对细胞作病理分析所观测到的信息,也就是所抽取到的d维观测向量。为简单起见,我们假定只用其一个特征进行分类,即d=1,并已知这两类的类条件概率密度函数分布已知,如图1所示,其中P(x|ω1)是正常细胞的属性分布,P(x|ω2)是异常细胞的属性分布。那末,当观测向量为X值时,它属于各类的概率又是多少呢?为此我们可以利用贝叶斯公式, 来计算这种条件概率,称之为状态的后验概率P(ωi|X)。
Bayes(贝叶斯)公式是根据联合概率这一概念推出的,同时出现两个事件X及ωi的概率为P(x,ωi)。它是某个条件出现的概率(如P(ωi)),以及在此条件下某事件出现概率(P(x|ωi))的乘积,在此写为:
P(x,ωi)=P(x|ωi)P(ωi)=P(ωi|x)P(x)
先验概率是针对ωi,I=1,2,…,c,这c个事件出现的可能性而言的,不考虑其它任何条件。例如世界上有60亿人口,而中国人口12亿,因此不管其它条件,应有20%的可能是中国人。类条件概率密度函数P(x|ωi)是指ωi条件下在一个连续的函数空间出现X的概率密度,在我们这里指第ωi类样本他的属性X是如何分布的。

- 如果
 ,则
,则 .............................. <2>
.............................. <2> - 如用先验概率及类条件概率密度函数表示,则有:
其中<4>式中的l(x)在统计学中称为似然比,而
=====例子1========
例: 假设在某地区切片细胞中正常(ω1)和异常(ω2)两类的先验概率分别为P(ω1)=0.9,P(ω2)=0.1。现有一待识别细胞呈现出状态x,由其类条件概率密度分布曲线查得p(x|ω1)=0.2,p(x|ω2)=0.4,试对细胞x进行分类。
解:利用贝叶斯公式,分别计算出状态为x时ω1与ω2的后验概率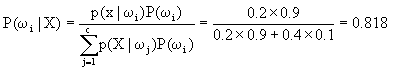 ,而
,而![]() .根据贝叶斯决策<2>则有P(ω1|x)=0.818>P(ω2|x)=0.0182.因此判定该细胞为正常细胞比较合理。我们注意一下,使用公式<3>与<5>计算,检查一下结果是否一样呢?
.根据贝叶斯决策<2>则有P(ω1|x)=0.818>P(ω2|x)=0.0182.因此判定该细胞为正常细胞比较合理。我们注意一下,使用公式<3>与<5>计算,检查一下结果是否一样呢?
================
从这个例子可以看出,尽管类别ω2呈现出状态x的条件概率要高于ω1类呈现此状态的概率,但是考虑到P(ω1)远大于P(ω2),因此状态x属于类别ω1的可能性远比属于类别ω2的可能性大。将该细胞判为正常在统计的意义上讲出错率要小得多。
为了搞清楚一些基本概念,我们还要强调一下条件概率这个概念。我们举出两对概率,一对是P(ω1|x)和P(ω2|x),另一对是P(x|ω1)和P(x|ω1)。从表面上看,只是条件符号两边的项对换了位置,但实质上却有很大区别。前一对是在同一条件x下,比较ω1与ω2出现的概率,如果我们只考虑两类ω1和ω2,则有P(ω1|x)+P(ω2|x)=1。而对两者进行数值上的比较,如P(ω1|x)> P(ω2|x)则可以下结论,在x条件下,事件ω1出现的可能性大。
对后一对概率来说,与第一对完全不同,因为它们是在不同条件下讨论的问题因此比较两者没有意义,而且即使只有两类ω1与ω2,P(x|ω1)+P(x|ω1)≠1。这里要特别强调一点是P(x|ω1)与P(x|ω2)两者没有联系,都是指各自条件下出现x的可能性,不能仅因为前者比后者大,就认为x是第一类事物的可能性较大,只有考虑先验概率这一因素,才能决定x条件下,ω1类还是ω2类的可能性比较大。
另外,为什么后验概率要利用Bayes公式从先验概率和类条件概率密度函数计算获得。这是因为计算概率都要拥有大量数据才行。在估计先验概率与类条件概率密度函数时都可搜集到大量样本,而对某一特定事件(如x)要搜集大量样本是不太容易的。因此只能借助Bayes公式来计算得到。
对基于最小错误率的贝叶斯决策来说,以后验概率值的大小作判据是最基本的方法,而其它形式的作用都基本相同,但使用时更方便些。
以上讨论的是在两类情况下基于最小错误概率的贝叶斯决策规则,下面需证明按这种规则进行分类确实使错误率为最小。下面仅以一维情况来证明,其结果并不难推广到多维的情况。
由于统计判别方法是基于统计参数作出决策,因此错误率也只能从平均的意义上讲,表示为在观测值可能取值的整个范围内错识率的均值。在连续条件下,平均错误率,以P(e)表示,应有
其中p(e,x)表示错误率为e观测值为x的联合概率密度,P(e|x)是观测值为x时的条件错误概率密度函数,P(x)为x值出现的概率,而积分运算则表示为在整个d维特征空间上的总和。在此一维情况下,x取从-∞到+∞的整个范围。
在两类别问题中,按<2>式给出的决策规则,当P(w2|x)>p(w1|x)时决策为w2。显然这个决策意味着,对观测值x有P(w1|x)概率的错误率。例如在上例中所作的w1决策,实际上包含有P(w2|x)=0.182的错误概率。在两类别的情况下,可以将p(e|x)表示成当
如果我们把作出w1决策的所有观测值区域称为R1,则在R1区内的每个x值,条件错误概率为p(w2|x)。另一个区R2中的x,条件错误概率为p(w1|x)。因此平均错误率P(e)可表示成
由于在R1区内任一个x值都有P(w2|x)<P(w1|x),同样在R2区内任一个x值都有P(w1|x)<P(w2|x)错误率在每个x值处都取小者,因而平均错误率P(e)也必然达到最小,这就证明了按<2>式作出的决策,其平均错误率为最小。
为了形象地说明以上证明,图3表示了在某种概率分布下R1与R2区的分布情况,该图分别画出p(x|ω1)P(ω1)及p(x|ω2)P(ω2)的分布情况,由于P(e)也可以<8>式写成
因此错误率为图中两个划线部分之和,显而易见只有这种划分才能使对应的错误率区域面积为最小。
以上讨论的是两类别问题情况,在C类别情况下,很容易写成相应的最小错误率贝叶斯决策规则:
至于计算多类别决策过程中的错误率,需把特征空间分割成R1,R2,…,Rc个区域,在每个区域Ri统计将所有其它类错误划为该区域对应的i类的概率,则每个区域共有c-1项错误率,总共有c(c-1)计算项,计算是很繁琐的。为此,可以改成计算平均正确分类概率P(c)即
由于上式中只有c项,计算要简单得多。然后通过式子P(e)=1-P(c),就可计算出平均错误率。
基于最小风险的贝叶斯决策
上面我们讨论了使错误率最小的贝叶斯决策规则。然而当接触到实际问题时,可以发现使错误率最小并不一定是一个普遍适用的最佳选择。譬如,在上面讨论过的细胞分类的例子中,把正常细胞错分为癌细胞,或相反方向的错误,其严重性是截然不同的。把正常细胞误判为异常细胞固然会给人带来不必要的痛苦,但若将癌细胞误判为正常细胞,则会使病人因失去及早治疗的机会而遭受极大的损失。由此可见,根据不同性质的错误会引起不同程度的损失这一考虑出发,我们宁肯扩大一些总的错误率,但也要使总的损失减少。这会引进一个与损失有关联的,更为广泛的概念——风险。在作出决策时,要考虑所承担的风险。基于最小风险的贝叶斯决策规则正是为了体现这一点而产生的。
在讨论基于风险的决策方法的具体内容之前,让我们首先回顾一下讨论的基于最小错误概率的决策方法。从式<10>可以看出,在分类时所作的判决(称之为决策)单纯取决于观测值X对各类(也称自然状态)的后验概率中之最大值,因而也就无法估计作出错误决策所带来的损失。为此不妨将作出判决的依据从单纯考虑后验概率最大值,改为对该观测值X条件下各状态后验概率求加权和的方式,表示成
其中![]() 表示观测样本X实属类别j,而被判为状态i时所造成的损失,Ri则表示了观测值X被判为i类时损失的均值。如果我们希望尽可能避免将某状态ωj,错判为状态ωi,则可将相应的
表示观测样本X实属类别j,而被判为状态i时所造成的损失,Ri则表示了观测值X被判为i类时损失的均值。如果我们希望尽可能避免将某状态ωj,错判为状态ωi,则可将相应的![]() 值选择得大些,以表明损失的严重性。加权和Ri用来衡量观测样本X被判为状态ωi所需承担的风险。而究竟将X判为何类则应依据所有Ri,(i=1,…,c)中的最小值,即最小风险来定。
值选择得大些,以表明损失的严重性。加权和Ri用来衡量观测样本X被判为状态ωi所需承担的风险。而究竟将X判为何类则应依据所有Ri,(i=1,…,c)中的最小值,即最小风险来定。
我们再从另一角度把这个问题说清楚。我们见到一个病理切片X,要确定其中有没有癌细胞(用ω1表示正常,ω2表示异常),则P(ω1|X)与P(ω2|X)分别表示了两种可能性的大小。如果X确实是癌细胞(ω2),但被判作正常(ω1),则会有损失,这种损失用![]() 表示,X确实是正常(ω1),却被判定为异常(ω2),则损失表示成
表示,X确实是正常(ω1),却被判定为异常(ω2),则损失表示成![]() ,另外为了使式子写的更方便,我们也可以定义
,另外为了使式子写的更方便,我们也可以定义![]() 与
与![]() ,是指正确判断也可有损失。那么把X判作ω1引进的损失应该与
,是指正确判断也可有损失。那么把X判作ω1引进的损失应该与![]() 以及
以及![]() 都有关,哪一个占主要成分,则取决于P(ω1|X)与P(ω2|X)。因此变成了一个加权和
都有关,哪一个占主要成分,则取决于P(ω1|X)与P(ω2|X)。因此变成了一个加权和
同样将X判为ω2的风险就成为
此时作出哪一种决策就要看是R1(X)小还是R2(X)小了,这就是基于最小风险的贝叶斯决策的基本出发点。有关该例的数值例子在例2。
以上讨论是为了说明这种方法的概念。下面我们给出一些确切的定义。
- 自然状态与状态空间。其中自然状态是指待识别对象的类别,而状态空间Ω则是由所有自然状态所组成的空间,Ω={ω1,ω2,…,ωc}
- 决策与决策空间。在决策论中,对分类问题所作的判决,称之为决策,由所有决策组成的空间称为决策空间。决策不仅包括根据观测值将样本划归哪一类别(状态),还可包括其它决策,如“拒绝”等,因此决策空间内决策总数a可以不等于类别数c,表示成
 .
. - 损失函数λ(αi|ωj)(或写成λ(αi,ωj))。这就是前面我们引用过的
 。它明确表示对自然状态ωj,作出决策αi时所造成的损失。
。它明确表示对自然状态ωj,作出决策αi时所造成的损失。 - 观测值X条件下的期望损失R(αi|X),
 ,i=1,2,…,a. .........<14>
,i=1,2,…,a. .........<14>
这就是前面引用的符号Ri,也称为条件风险。与式<10>类似,最小风险贝叶斯决策规则可写成:
如果
,则α=αk ...................<15>
但与<10>式不同的是,这里计算的是最小值。与上一小节中基于最小错误概率的决策方法中所引用的平均错误率P(e)相类似,在这里引入一个期望风险R,
它表示对所有X取值所作的决策α(X)所带来的平均风险。与上一节证明基于最小错误概率的贝叶斯决策方法相类似,当所采取的每一个决策都使其条件风险最小,则对所有的X所作的决策,其期望风险也必然最小。
对于实际问题,最小风险贝叶斯决策可按下列步骤进行:
a). 在已知P(ωi),P(X|ωi),i=1,…,c及给出待识别的X的情况下,根据贝叶斯公式计算出后验概率:
b). 利用计算出的后验概率及决策表,按式<14>计算出采取αi,i=1,…,a的条件风险.
c). 对b)中得到的a个条件风险值R(αi|X),i=1,…,a进行比较,找出使条件风险最小的决策αk,即
则αk就是最小风险贝叶斯决策。
======例子2============
在例1条件的基础上,并且已知λ11=0,(λ11表示λ(α1|ω1)的简写),λ12=6,λ21=1,λ22=0,按最小风险贝叶斯决策进行分类。
解:已知条件为
P(ω1)=0.9, P(ω12)=0.1;
p(X|ω1)=0.2, p(X|ω12)=0.r;
λ11=0, λ12=6, λ21=1, λ22=0
根据<1>的计算结果可知后验概率为P(ω1|X)=0.818, P(ω12|X)=0.182
再按式<14>计算出条件风险
由于R(α1|X)>R(α2|X),即决策为ω12的条件风险小于决策为ω1的条件风险,因此应采取决策行动α2,即判待识别的细胞X为ω12类------异常细胞。
将本例与例1相对比,其分类结果正好相反,这是因为影响决策结果的因素又多了一个“损失”。由于两类错误决策所造成的损失相差很悬殊,因此“损失”在这里起了主导作用。
===============
从以上讨论可以看出,正确制订损失函数值,是基于最小风险的贝叶斯决策方法在实际中使用的一个关键问题。而实际中列出合适的决策表并不是一件容易的事,需根据所研究的具体问题,分析错误决策造成损失的严重程度,与有关专家共同商讨来确定。
再讨论一下上面两种决策方法之间的关系,设损失函数为
式中假定对C类只有C个决策,即不考虑“拒绝”等其它情况,(2-17)表明,当作出正确决策(即i=j)时没有损失,而对于任何错误决策,其损失均为1。这样定义的损失函数称为0—1损失函数。
根据<14>式条件风险为
而![]() 也恰恰是将X判为ω1i时的错误概率。因此基于最小风险的贝叶斯决策结果,在0-1损失函数情况下,也就是基于最小错误概率的贝叶斯决策结果。由此可见,最小错误率贝叶斯决策就是在0-1损失函数条件下的最小风险贝叶斯决策。实际上
也恰恰是将X判为ω1i时的错误概率。因此基于最小风险的贝叶斯决策结果,在0-1损失函数情况下,也就是基于最小错误概率的贝叶斯决策结果。由此可见,最小错误率贝叶斯决策就是在0-1损失函数条件下的最小风险贝叶斯决策。实际上 ,因此,当
,因此,当![]() 最大时
最大时![]() 最小.它与基于最小错误率的贝叶斯决策的判据是一样的。如果我们只考虑两类别问题,并只有一维特征向量的情况,我们可以画出一张与图3类似的图4,用来表示最小风险贝叶斯决策方法的分类结果。与图3不同的是,R1与R2两个区域的分界线不再是t,而是向左移了一段距离,这是由于损失函数λ12比λ21大所造成(可以假设λ11=λ22=0),在发生位移这一区域内,尽管P(x|ω1)P(ω1)>P(x|ω12)P(ω12),但是为了减少将ω12错判为ω1所带来的严重损失,在P(x|ω12)P(ω12)尚不很小的情况下,使将ω12类样本错判为ω1的可能性减小,以减小决策所承担的风险。当然平均错误率则明显增大了。
最小.它与基于最小错误率的贝叶斯决策的判据是一样的。如果我们只考虑两类别问题,并只有一维特征向量的情况,我们可以画出一张与图3类似的图4,用来表示最小风险贝叶斯决策方法的分类结果。与图3不同的是,R1与R2两个区域的分界线不再是t,而是向左移了一段距离,这是由于损失函数λ12比λ21大所造成(可以假设λ11=λ22=0),在发生位移这一区域内,尽管P(x|ω1)P(ω1)>P(x|ω12)P(ω12),但是为了减少将ω12错判为ω1所带来的严重损失,在P(x|ω12)P(ω12)尚不很小的情况下,使将ω12类样本错判为ω1的可能性减小,以减小决策所承担的风险。当然平均错误率则明显增大了。
图中绿线为分类线,左边被识别为第1类,右边为第2类,两条曲线为概率分布曲线,绿线左侧红线以下表示把第二类错分为第一类的可能性,另一块灰色区域含义类似。整个灰色区域加权后可以表示风险。可以考虑用applet实现交互演示,用户可以拖动分类面的位置,计算并显示风险大小,可以找到风险最小的分界面。式<13>定义了样本为X作出i决策时的期望风险,可以从两个方面理解。一种是由于样本存在分属各类的可能性,而对实属一类却决策成i类会造成程度不同的损失,因而期望损失应是风险系数![]() 与
与![]() 相乘之总和。另一种看法可以将损失看成是对后验概率的重要性作加权,
相乘之总和。另一种看法可以将损失看成是对后验概率的重要性作加权,![]() 是对
是对![]() 的加权系数。因此只要 稍大一点,就会使风险明显增大。公式<17>与<18>说明了基于最小错误率与基于最小风险两种Bayes决策的关系,结论是基于最小错误率的决策是基于最小风险决策的一个特例。这是因为后者多了一些系数允许调整,而按<17>式调整就将基于最小风险决策改成基于最小错误率决策,这种设置可调整参数集的情况比限定参数集的情况有更大自由度因此后者必定为前者的一个特定情况。
的加权系数。因此只要 稍大一点,就会使风险明显增大。公式<17>与<18>说明了基于最小错误率与基于最小风险两种Bayes决策的关系,结论是基于最小错误率的决策是基于最小风险决策的一个特例。这是因为后者多了一些系数允许调整,而按<17>式调整就将基于最小风险决策改成基于最小错误率决策,这种设置可调整参数集的情况比限定参数集的情况有更大自由度因此后者必定为前者的一个特定情况。
在限定一类错误率条件下使另一类错误率为最小的两类别决策
上面讨论的最小错误率或最小风险决策方法都是在先验概率已知的条件下进行的,先验概率的数值对决策有很密切的关系。然而有时会遇到先验概率不知道,或先验概率发生变化的情况。在这种情况下,如果仍按某一组先验概率值P(ωi)作决策,则很可能使实际的决策效果有较大的错误率或较大风险。那末能否在这种情况下,找到一种合适的分类器设计,使其最大可能的风险为最小。换句话说,如果先验概率值在较大范围内变化,就可能产生的最大风险而言是最小的。而本节讲的是哪一种办法,即不考虑先验概率,而只要求限定某一种错误率条件下,使另一类错误率最小。
在前面的讨论中,曾提到在两类别问题中,可能会出现两种错误分类的情况。利用式<9>,平均错误率P(e)可按下式计算![]() .如令
.如令![]() 及 ,则上式又可写成
及 ,则上式又可写成
...................<19>
......................<20>
其中R1与R2分别是ω1与ω2的决策域,而R1与R2组成整个特征空间R,且彼此互不交迭。因此如果被识别样本X落入R1中,就被判定为ω1,反之属ω2。由于R1与R2不相交并组成整个特征空间,应有
........................<23>
将式<21>,式<22>代入式<20>,并考虑到式<23>可得
 ...............................................<25>、<26>
...............................................<25>、<26>
式<25>与式<26>的方程式就决定了这样一个分界面λ,它使P2(e)=ε0,同时又在该条件下使P1(e)尽可能小。该分界面上X值具有这样一个特点,即它们的两类条件密度函数之比是一个常数,该比值就是拉格朗日乘子。这种决策规则可写成:
这种在限定某一类错误为常数而使另一类错误率最小的决策也称Neyman-Pearson决策规则。如果将<28>与最小错误率决策规则<24>相对比,可以看出Neyman-Pearson决策规则也是以似然比为基础的,但两者所使用的阈值不同。最小错误率决策使用![]() 为阈值,而Neyman-Pearosn决策则使用由<25>与<26>方程的解获得的一个常数λ。式<25>与<26>提供了该种决策的决策面方程,但在高维时,即d较大时,直接求解是不容易的。一般可利用P2(e)与λ值之间存在的单调函数关系,采用选择一些λ值的试探法,最终找到一合适的λ值,既能使P2(e)=ε0条件满足,又能使P1(e)尽可能小。
为阈值,而Neyman-Pearosn决策则使用由<25>与<26>方程的解获得的一个常数λ。式<25>与<26>提供了该种决策的决策面方程,但在高维时,即d较大时,直接求解是不容易的。一般可利用P2(e)与λ值之间存在的单调函数关系,采用选择一些λ值的试探法,最终找到一合适的λ值,既能使P2(e)=ε0条件满足,又能使P1(e)尽可能小。
判别函数、决策面与分类器设计
以上我们讨论了几种常用的决策原则,在这些原则的指导下,可以进行分类器的设计。在讨论分类器设计前,需要说明在分类器设计中使用的一些概念,这就是决策面与判别函数。曾提到,分类决策实质上是在描述待识别对象的d维特征所组成的特征空间内,将其划分为c个决策域,待识别的特征向量落在哪个决策域,该样本就被判为哪一类。因此决策域的边界面就是决策面,在数学上用解析形式表示成决策面方程。用于表达决策规则的某些函数则称为判别函数。显然判别函数与决策面方程是密切相关的,并且都是由相应决策规则所确定的。
在两类别问题中,按最小错误率作决策时,决策规则的一种形式是![]() ,否则
,否则![]() 则相应的判别函数就是: gi(X)=P(ωi|X), i=1,2.而决策面方程则可写成: g1(X)=g2(X).此时决策规则也可以写成用判别函数表示的形式:如果gi(X)>gj(X) i,j=1,2 且 i≠j 则X∈ωi,否则
则相应的判别函数就是: gi(X)=P(ωi|X), i=1,2.而决策面方程则可写成: g1(X)=g2(X).此时决策规则也可以写成用判别函数表示的形式:如果gi(X)>gj(X) i,j=1,2 且 i≠j 则X∈ωi,否则![]() .至于多类别情况,则对应于一种决策规则要定义一组判别函数gi(X), i=1,2,…,c. 而决策规则可表示成: 如果
.至于多类别情况,则对应于一种决策规则要定义一组判别函数gi(X), i=1,2,…,c. 而决策规则可表示成: 如果![]() ,则将X归于ωi类;
,则将X归于ωi类;
多类别情况下的决策面方程比两类问题复杂,并且只有在特征空间中具有相邻关系的决策域的边界面才是有意义的决策面。当ωi的决策域与ωj的决策域相邻时,以下关系决定了相应的决策面gi(X)=gj(X).此外,决策面是一种统称,当特征空间只是一维时,一个决策面实际上只是一个点。在二维特征空间里,决策面是一条曲线。三维则是一曲面,超过三维的空间,决策面是一个超曲面。图5(a)表示了一个三类别问题用一维特征空间时的所有决策边界,而图5(b)则表示了相应的二维特征空间中的决策边界。
在讨论了判别函数等概念后,设计分类器的任务就清楚了。分类器可以用软件或硬件实现。图6表示了两类别问题分类器的框图,
而图7则表示了多类别分类器的结构框图。两者主要的不同在于多类别情况需有一个求最大值的环节,在图7中用MAX表示,而两类情况则可简化为正负号判别器(阈值单元)。
[注:图5,图6,图7,来自于网络]
分类器设计除了确定结构框图外,问题主要集中在判别函数的选择,使用最小风险决策时合理的损失函数的确定。此外贝叶斯决策理论都是基于统计分布确定的情况下的计算,而统计参数的确定恰恰是最困难的问题。如果要按贝叶斯决策方法设计分类器,就必须设法获得必需的统计参数。
前面讨论的Bayes决策理论其实是很简单的,对特征空间任一点X只要能确定落在该点的样本X属于哪一种类的可能性大,就将这点划分到这类的决策域。问题是后验概率P(ωi|X)要通过先验概率和类概率密度函数计算。因为Bayes决策是一种通用方法,它只在原理上讲特征空间中符合什么条件才能作为哪一类决策域,而我们希望能把决策域用简便的方式,最好是函数形式划分出来,直接计算判别函数就方便了。显然具体的决策域划分与样本的概率分布有关。
参考资料
[1] R.O.Duda, P.E.Hart. Pattern Classification and Scene Analysis.NewYork: John wiley & sons. 1973.
[2] Nello Cristianini & Jogn Shawe – Jaylor. An Introduction to Support Vector Machines and other Kernel – based learning method. Cambridge University Press 2000.
[3] Fukunaga, Keinosuke (1990).Introduction to Statistical Pattern Recognition (2nd ed.). Boston: Academic Press. ISBN 0-12-269851-7.
[4] Bishop, Christopher (2006). Pattern Recognition and Machine Learning. Berlin: Springer. ISBN 0-387-31073-8.
[5] Koutroumbas, Konstantinos; Theodoridis, Sergios (2008).Pattern Recognition (4th ed.). Boston: Academic Press. ISBN 1-59749-272-8.
[6] Hornegger, Joachim; Paulus, Dietrich W. R. (1999).Applied Pattern Recognition: A Practical Introduction to Image and Speech Processing in C++ (2nd ed.). San Francisco: Morgan Kaufmann Publishers. ISBN 3-528-15558-2.
[7] Schuermann, Juergen (1996).Pattern Classification: A Unified View of Statistical and Neural Approaches. New York: Wiley. ISBN 0-471-13534-8.
[8] An introductory tutorial to classifiers (introducing the basic terms, with numeric example)
[9] Godfried T. Toussaint, ed. (1988).Computational Morphology. Amsterdam: North-Holland Publishing Company.
[10] The International Association for Pattern Recognition
[11] List of Pattern Recognition web sites
[12] Journal of Pattern Recognition Research
关于Meachine Learning&Pattern Recognition更多讨论与交流,敬请关注本博客和新浪微博songzi_tea.