VINS理论与代码详解4——初始化

VINS理论与代码详解4——初始化

1.      基于滑动窗口的纯视觉单目初始化

    在介绍纯视觉初始化前我们首先讲一讲为什么要初始化？初始化要做什么？以及初始化的作用？我们初始化的原因是单目惯性紧耦合系统是一个非线性程度很高的系统，首先单目是无法获得空间中的绝对尺度，而IMU又必然存在偏置，在后面进行求解的时候还需要用到重力加速度（包括大小和方向），对于速度比较敏感的条件下，比如说无人机，又要精确的速度信息，因此，如何有效的在紧耦合系统处理之前计算出这些量，对整个紧耦合系统的鲁棒性有着重大的意义（其实这里就可以理解成相机标定一样，没有正确的标定好相机的内参，相机在进行定位的时候必然不准，而且很有可能会挂掉）。所以初始化要做的事其实说起来很简单，就是计算出绝对尺度s、陀螺仪偏置bg、加速度偏置ba、重力加速度G和每个IMU时刻的速度v，VINS中重点说明了加速度计偏置值一般都会和重力加速度耦合到一起（也就是被重力加速度给吸收掉），重力加速度的量级要远大于其加速度偏置，而且在初始化时间内加速度计偏置比较小，很难真正的计算得到，因此忽略加速度计偏置的影响，在初始化中不再计算。初始化的作用是不言而喻的，直接影响整个紧耦合系统的鲁棒性以及定位精度，并且初始化一般都需要一个比较漫长的时间，VINS大概需要十秒左右，ORB_SLAM2结合IMU的时间设定在15秒完成初始化。话不多说，直接进入正题。

         纯视觉初始化在第V点的A部分，首先构建一个滑动窗口，包含一组数据帧。论文中提及使用的是对极几何模型的5点法求解单目相机的相对变换，包括相对旋转和无尺度信息的位移。其实基本上每个单目模型都是使用对极几何在初始化中求解两帧的相对变换，这里需要注意的是旋转是具有尺度不变性的（其实就是单位旋转，不会有尺度信息，你仔细想想是不是？）。然后三角化得到相应的3d点坐标，有这些3d点和滑动窗口中其他的帧的2d点就可以进行PNP求解获得滑动窗口中的所有的位姿和特征点3d坐标，至此，纯视觉初始化就完成了。是不是很简单？当然啊，毕竟只是简单的视觉初始化，而真正复杂的是视觉惯性联合初始化，也就是我们初始化的重点和难点，所以下面的知识点一定要打起精神学啦！

 

2.      视觉惯性联合初始化

    视觉惯性联合初始化在第V点的B部分，这里作者给定义的名字叫Visual-Inertia Alignment，即视觉惯性联合初始化（而在ORBSLAM2+IMU的论文里，作者定义的名称就叫IMU initialization，即IMU初始化），为什么定义这样一个名词，我觉得有两个意义，第一在进行陀螺仪偏置初始化的时候要同时使用到IMU测量的旋转和视觉测量的旋转，也就是要联合视觉和惯性的数据。第二这里求得的尺度S的值不仅仅是IMU的，还是视觉和IMU整个系统的尺度。在具体的讲解初始化每个过程的时候，有必要来个总体的概括，初始化在物理意义上的定义其实就是固有参数的标定，在数学模型上的定义其实就是公式（6）的矩阵方程求解，而公式（6）其实就是来自于最原始的PVQ积分公式，其中Q旋转对应着陀螺仪，而PV对应着加速度计，如果不明白的话，不要紧，看完下面的整体推导过程相信聪明的你一定会茅塞顿开。

（1）      陀螺仪偏置标定

旋转我们可以通过两种方式求得，一种是陀螺仪测量值，一种就是视觉观测值。按照正常的理解两者的大小一定是相等的（假设没有误差），但实际情况肯定有误差，我们就来看看各自的误差。陀螺仪的误差有两部分测量噪声和陀螺仪偏置，噪声暂时可以忽略（毕竟太小），而视觉的误差就只有观测噪声（也可以忽略不管），因此两者差值的绝对值就是陀螺仪偏置，将整个滑动窗口的所有的旋转做差构成了一个最小化误差模型：

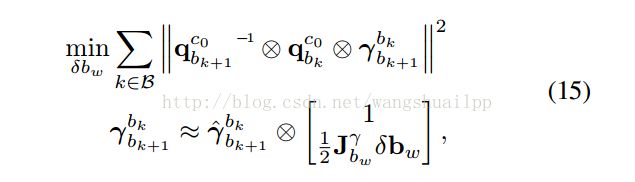
    公式15中第一个式子的第一项和第二项作四元数旋转的广义乘积就可以得到相机从bk到bk+1下的相对旋转（bk+1坐标系下），第三项是陀螺仪从bk+1到bk下的相对旋转（bk坐标系下），两者在做广义乘积，就是首先从bk到bk+1旋转，然后再从bk+1到bk旋转，相当于做差（OA+AO=0），第二个式子就是前面预积分提到的一阶线性近似。然后取最小二乘，当然也可以使用SVD分解等方法求解。注意在求得陀螺仪偏置之后要再次将陀螺仪偏置代入到预积分中再求一次预积分的值，会更加精确。

（1）      速度、重力加速度和尺度标定

作者在这里将这三个状态量统一到一个状态向量中，如公式16所示：

速度的是在bk坐标系下的，重力加速度在初始相机坐标系下，就像前面提到的，求解着几个量是由P、V数学模型求得，在滑动窗口中考虑到两个连续关键帧bk和bk+1，下面进行论文中公式17和19的推导：

    公式推导之后就会得到论文中的公式17、18和19，我们重点关注下为什么要这样推导，以及推导得到的运动方程关系。首先为什么要进行这样的推导，这完全取决于状态向量的定义方式，我们最终要得到的方程形式左边一定是以状态向量的形式来表达的，而且还要满足其他量都是已知的（从IMU预积分和视觉跟踪得到），因此就需要将方程进行如此的变化，才能满足这样的关系。然后是最后的形式我们可以看到状态向量最终的形式维度是（n+1）*3+3+1，两个连续帧产生的运动方程的维度是3+3+3+1（vbkbk，vbk+1bk+1，gc0，s），比较维度就可以看到最终得到的H矩阵一定是一个正定对称矩阵，因此可以采用快速的Cholesky分解。

 

（1）      重力优化

    上面其实已经得到了重力加速度的大小和方向，这里为什么还需要对重力进行优化呢？理由很简单，这里计算的重力吸收了重力加速度计的偏置，虽然不需要计算重力加速度计的偏置，但重力还是需要优化的，说到优化重力加速度，肯定包含两个量，大小和方向，也就是三个维度，但是一般来说大小是确定已知的（这里设为9.8），因此其实我们要做的就是优化方向，是一个两维的向量，下图是优化重力的方法以及b1,b2单位向量的方向确定模型。

 代码详解：

注：上接IMU预积分

步骤2：处理图像特征数据

这里进来的数据不是图像数据哦，而是前面已经跟踪匹配好的归一化平面坐标。将当前帧的特征存放在image中，image的第一个元素类型是相机的编号，代表是第几帧图像（从0开始），第二个元素是归一化特征点坐标和特征点编号（从1开始），然后直接进入到处理图像特征数据的线程中estimator.processImage(image, img_msg->header)。

1）Estimator::processImage(constmap>> &image, conststd_msgs::Header &header)处理图像特征数据方法

         首先对进来的图像特征数据根据视差判断是否是关键帧，选择丢弃当前帧（但保留IMU数据）或者丢弃滑动窗口中最老的一帧。

步骤1：将图像数据和时间存到图像帧类中：首先将数据和时间保存到图像帧的对象imageframe中（ImageFrame对象中包含特征点，时间，位姿R，t，预积分对象pre_integration，是否是关键帧）,同时将临时的预积分值保存到此对象中（这里的临时预积分初值就是在前面IMU预积分的时候计算的），然后将图像帧的对象imageframe保存到all_image_frame对象中（imageframe的容器），更新临时预积分初始值。

步骤2：标定相机和IMU的外参数：接着如果没有外部参数就标定外部参数，参数传递有的话就跳过这一步（默认有，如果是自己的设备，可以设置为2对外参进行在线标定）。

步骤3：初始化系统同时进行BA优化：当求解器处于可初始化状态时（初始状态是可初始化，初始化成功就设置为不可初始化状态），判断当前frame_count是否达到WINDOW_SIZE，确保有足够的frame参与初始化，这里的frame_count是滑动窗口中图像帧的数量，一开始被初始化为0，滑动窗口总帧数是10。有外部参数同时当前帧时间戳大于初始化时间戳0.1秒，就进行初始化操作。

步骤3.1：initialStructure()系统初始化，首先初始化Vision-only SFM，然后初始化Visual-Inertial Alignment，构成整个初始化过程。

①保证IMU充分运动，通过线加速度判断，一开始通过线加速度的标准差（离散程度）判断保证IMU充分运动，加速度标准差大于0.25则代表imu充分激励，足够初始化。

②纯视觉初始化，对SlidingWindow中的图像帧和相机姿态求解sfm问题，这里解决的是关键帧的位姿和特征点坐标。

步骤1.首先构建SFMFeature对象sfm_f，SFMFeature数组中包含了特征点状态（是否被三角化），id，2d点，3d坐标以及深度，将特征管理器中的特征信息保存到SFMFeature对象sfm_f中sfm_f.push_back(tmp_feature)。

步骤2.接着由对极约束中的F矩阵恢复出R、t，主要调用方法relativePose(relative_R, relative_T, l)。relativePose方法中首先通过FeatureManeger获取（滑动窗口中）第i帧和最后一帧的特征匹配corres，当corres匹配足够大时，考察最新的keyFrame和sliding window中某个keyFrame之间有足够feature匹配和足够大的视差（id为l=i），满足这两个条件，然后这两帧之间通过五点法恢复出R，t并且三角化出3D的特征点feature point，这里是使用solveRelativeRT(corres, relative_R, relative_T)，solveRelativeRT方法定义在solv_5pts.cpp类中，由对极约束中的F矩阵恢复出R、t，直接调用opencv中的方法，没什么好说的， 这里值得注意的是，这种 relativePose 得到的位姿是第 l 帧的，第 l 帧的筛选是从第一帧开始到滑动窗口所有帧中一开始满足平均视差足够大的帧，这里的第 l 帧会作为参考帧到下面的全局 SFM 使用。到这里就已经得到图像的特征点2d坐标的提取，相机第l帧和最后一帧之间的旋转和平移（注意暂时还没有得到特征的3d点坐标），有了这些信息就可以构建全局的SFM类GlobalSFM sfm，在这里调用sfm.construct(frame_count + 1, Q, T,l,relative_R, relative_T,sfm_f, sfm_tracked_points)，这里以第l帧作为参考帧，在进行PNP求解之前，需要判断当前帧数要大于第l帧，这保证了第l帧直接跳过PNP步骤， 首先执行下面的第 l 帧和最后一帧的三角化，得到共视的特征点，供下面第l+1帧和最后一帧求解PNP，然后利用pnp求解l+1帧到最后一帧的位姿R_initial, P_initial，最后的位姿都保存在Pose中，一次循环，得到l+1，l+2…n-1帧的位姿。跳出步骤2 的循环后，至此得到了l+1，l+2…n-1帧的位姿以及l+1，l+2…帧与n-1帧的特征点三角化。然后再三角化l帧和i帧（在第l帧和最后一帧之间的帧）之间的3d坐标，（这里不明白为什么要做两次，是可以三角化出更多的特征点吗？？？？），接着PNP求解l-1，l-2…0帧和l帧之间的位姿已经三角化相应的特征点坐标，最后三角化其他所有的特征点。至此得到了滑动窗口中所有相机的位姿以及特征点的3d坐标。第6部就是进行BA优化，使用的是ceres优化位姿和特征点，这里可以参考视觉SLAM第十讲中的内容，优化方式相同。

步骤4：visualInitialAlign中调用VisualIMUAlignment方法，真正的视觉惯性联合初始化，imu与视觉对齐，获取绝对尺度等。这个方法定义在initial/initial_alignment.h中。

步骤4.1：solveGyroscopeBias计算陀螺仪偏置，整个方法的计算模型由论文中给出，使用LTLD方法求解最小二乘问题，delta_bg = A.ldlt().solve(b);这里A +=tmp_A.transpose() * tmp_A，b += tmp_A.transpose() * tmp_b，其实就是处理AT*A*x=AT*b问题，一般的最小二乘问题直接处理Ax=b也就是Ax-b=0即可，这里是使用LDLT方法，两边同乘以A矩阵的转置得到的AT*A一定是可逆的，因此就可以直接两边同乘以其逆即可，相应的说明详见LDLT方法。得到陀螺仪偏置之后将其值保存到前面定义的Bgs[]中，最后在重新计算一次预积分。

步骤4.2：LinearAlignment计算尺度，重力加速度和速度。论文中给出的公式是相邻两个速度的模型，映射到整个n+1个速度模型中，A矩阵一定是一个正定矩阵（实对称矩阵），代码中定义的A和b即是最总的H和b，tmp_A和tmp_b相邻速度间的临时变量。最后的求解方法：x = A.ldlt().solve(b)；然后调用RefineGravity重新计算重力加速度方向，得到最优解。