题目传送门
是一道十分经典的LCS问题
很容易想到 n2 的一般算法:
主题代码如下:
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++){
dp[i][j] = max (dp[i-1][j], dp[i][j-1]);
if (a[i] == b[j]) dp[i][j] = max (dp[i][j], dp[i-1][j-1] + 1);
}
printf ("%d", dp[n][n]); 但往下看一眼数据范围 :
没错, n ≤100000 ,n²直接TLE
题目描述中提到了两组数都是 自然数1-n的一个排列
所以这题可以这么来做:
设两个数组分别为 a 和 b
对于每一个a数组中的数,一定有一个唯一对应的相等的b数组中的数
可以将a数组中的数看作 1,2,3,4,5......n
将b数组中的数也变为对应的值,假设变为数组c,可以发现,这变成了一个最长上升子序列LIS问题
当c中的数有一个上升子序列时,则这个序列在原数组中一定与a数组是公共的
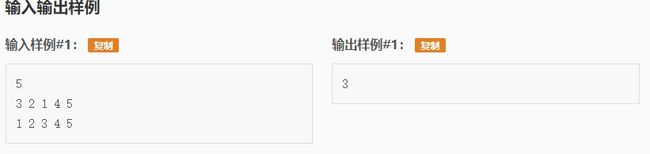
先把第一列数看作 1, 2, 3, 4, 5。 则3对应1, 2对应2, 1对应3 .......
第二列数变为 3, 2, 1, 4, 5
最长上升子序列为 1, 4, 5 或 2, 4, 5或3, 4, 5
可以发现,这三个序列在原数组中都能找到相应的公共部分
所以答案为3
完整代码:
#include
using namespace std;
#define f(i, r) for (int i = 1; i <= r; i++)
int n, x, a[100005], k[100005], len, q[100005];
int main(){
scanf ("%d", &n);
f (i, n) scanf ("%d", &x), k[x] = i;
f (i, n) scanf ("%d", &a[i]), a[i] = k[a[i]];
f (i, n){
if (a[i] > q[len]) q[++len] = a[i];
else{
int w = upper_bound (q + 1, q + len + 1, a[i]) - q;
q[w] = a[i];
}
}
printf ("%d", len);
return 0;
}
点一下左边的推荐吧!谢谢~~~