布隆过滤器
这名词有没有听着好像很 挺高大上的,的确,它也是一种很重要的结构,下面一起看看:
一:说说历史:
(Bloom Filter)是由布隆(Burton Howard Bloom)在1970年提出的。它实际上是由一个很长的二进制向量和一系列随机映射函数组成,布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都远远超过一般的算法,缺点是有一定的误识别率(假正例False positives,即Bloom Filter报告某一元素存在于某集合中,但是实际上该元素并不在集合中)和删除困难,但是没有识别错误的情形(即假反例False negatives,如果某个元素确实没有在该集合中,那么Bloom Filter 是不会报告该元素存在于集合中的,所以不会漏报)。
在日常生活中,包括在设计计算机软件时,我们经常要判断一个元素是否在一个集合中。比如在字处理软件中,需要检查一个英语单词是否拼写正确(也就是要判断 它是否在已知的字典中);
在 FBI,一个嫌疑人的名字是否已经在嫌疑名单上;在网络爬虫里,一个网址是否被访问过等等。最直接的方法就是将集合中全部的元素存在计算机中,遇到一个新 元素时,将它和集合中的元素直接比较即可。一般来讲,计算机中的集合是用哈希表(hash table)来存储的。它的好处是快速准确,缺点是费存储空间。当集合比较小时,这个问题不显著,但是当集合巨大时,哈希表存储效率低的问题就显现出来 了。
比如说,一个象 Yahoo,Hotmail 和 Gmai 那样的公众电子邮件(email)提供商,总是需要过滤来自发送垃圾邮件的人(spamer)的垃圾邮件。一个办法就是记录下那些发垃圾邮件的 email 地址。由于那些发送者不停地在注册新的地址,全世界少说也有几十亿个发垃圾邮件的地址,将他们都存起来则需要大量的网络服务器。如果用哈希表,每存储一亿 个 email 地址, 就需要 1.6GB 的内存(用哈希表实现的具体办法是将每一个 email 地址对应成一个八字节的信息指纹,然后将这些信息指纹存入哈希表,由于哈希表的存储效率一般只有 50%,因此一个 email 地址需要占用十六个字节。一亿个地址大约要 1.6GB, 即十六亿字节的内存)。因此存贮几十亿个邮件地址可能需要上百 GB 的内存。除非是超级计算机,一般服务器是无法存储的[2]。(该段引用谷歌数学之美:http://www.google.com.hk/ggblog/googlechinablog/2007/07/bloom-filter_7469.html)
二:概念:
如果想判断一个元素是不是在一个集合里,一般想到的是将所有元素保存起来,然后通过比较确定。链表,树等等数据结构都是这种思路.但是随着集合中元素的增加,我们需要的存储空间越来越大,检索速度也越来越慢。不过世界上还有一种叫作散列表(又叫哈希表,Hash table)的数据结构。它可以通过一个Hash函数将一个元素映射成一个位阵列(Bit Array)中的一个点(关于位阵列,即数据结构位图,详见位图见我另一篇博客:位图BitMap)。这样一来,我们只要看看这个点是不是 1就知道可以集合中有没有它了。这就是布隆过滤器的基本思想。
Hash面临的问题就是冲突。假设 Hash 函数是良好的,如果我们的位阵列长度为 m 个点,那么如果我们想将冲突率降低到例如 1%, 这个散列表就只能容纳 m/100 个元素。显然这就不叫空间有效了(Space-efficient)。解决方法也简单,就是使用多个 Hash(如下图所示),如果它们有一个说元素不在集合中,那肯定就不在。如果它们都说在,虽然也有一定可能性它们在说谎,不过直觉上判断这种事情的概率是比较低的。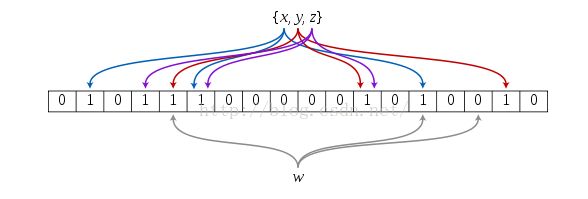
代码:
bitmap.h
#ifndef _BIT_MAP_H
#define _BIT_MAP_H
#include
#include
using namespace std;
/*
*一个数据32位,40亿个整数,每个整数需用一位表示,40亿位就完事
*/
class BitMap
{
public:
BitMap()
:_size(0)
{}
BitMap(size_t size)
:_size(0)
{
_array.resize((size>>5)+1); //多少个数据,一个数据占32位,加一是至少一个数据
}
bool Set(size_t num)
{
size_t index = num >> 5; //计算在哪个数据上
size_t n = num % 32;
if (_array[index] & (1 << (31 - n))) //移位问题
{
cout << "有数据" << endl;
return false;
}
else
{
size_t a = 1 << (31 - n);
_array[index] |= a;
++_size;
return true;
}
}
bool ReSet(size_t num) //删除一个数 之后重置
{
size_t index = num >> 5;
size_t n = num % 32;
if (_array[index] & (1 << (31 - n))) //数存在 删除
{
_array[index] &= (~(1 << (31 - n)));
--_size;
return true;
}
else
{
return false; //不存在这个数
}
}
private:
vector _array; //数组
size_t _size; //位图中数据个数
};
#endif
void Test()
{
BitMap bm(65);
for (int i = 0; i < 32; ++i)
{
bm.Set(i);
}
bm.ReSet(0);
} #pragma once
template //各类哈希函数
size_t BKDRHash(const char *str)
{
register size_t hash = 0;
while (size_t ch = (size_t)*str++)
{
hash = hash * 131 + ch;
}
return hash;
}
template
size_t SDBMHash(const char *str)
{
register size_t hash = 0;
while (size_t ch = (size_t)*str++)
{
hash = 65599 * hash + ch;
}
return hash;
}
template
size_t RSHash(const char * str)
{
size_t hash = 0;
size_t magic = 63689;
while (size_t ch = (size_t)*str++)
{
hash = hash * magic + ch;
magic *= 378551;
}
return hash;
}
template
size_t APHash(const char *str)
{
register size_t hash = 0;
size_t ch;
for (long i = 0; ch = (size_t)*str++; i++)
{
if ((i & 1) == 0)
{
hash ^= ((hash << 7) ^ ch ^ (hash >> 3));
}
else
{
hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));
}
}
return hash;
}
template
size_t JSHash(const char* str)
{
if (!*str)
{
return 0;
}
size_t hash = 1315423911;
while (size_t ch = (size_t)*str++)
{
hash ^= ((hash << 5) + ch + (hash >> 2));
}
return hash;
} #pragma once
#include"BitMap.h"
#include"HashFun.h"
template
struct __HashFun1 //5种哈希函数对应的仿函数
{
size_t operator()(const T& key)
{
return BKDRHash(key.c_str());
}
};
template
struct __HashFun2
{
size_t operator()(const T& key)
{
return SDBMHash(key.c_str());
}
};
template
struct __HashFun3
{
size_t operator()(const T& key)
{
return RSHash(key.c_str());
}
};
template
struct __HashFun4
{
size_t operator()(const T& key)
{
return APHash(key.c_str());
}
};
template
struct __HashFun5
{
size_t operator()(const T& key)
{
return JSHash(key.c_str());
}
};
template,
class HashFun2 = __HashFun2,
class HashFun3 = __HashFun3,
class HashFun4 = __HashFun4,
class HashFun5 = __HashFun5>
class Bloom_Filter
{
public:
Bloom_Filter(size_t size)
:_capacity(size)
{
_bitmap._array.resize((size >> 5) + 1);
}
void _Set(const K& key)
{
_bitmap.Set(HashFun1()(key) % _capacity);
_bitmap.Set(HashFun2()(key) % _capacity);
_bitmap.Set(HashFun3()(key) % _capacity);
_bitmap.Set(HashFun4()(key) % _capacity);
_bitmap.Set(HashFun5()(key) % _capacity);
}
bool _IsIn(const K& key)
{
if (!_bitmap.Test(HashFun1()(key) % _capacity))
return false;
if (!_bitmap.Test(HashFun1()(key) % _capacity))
return false;
if (!_bitmap.Test(HashFun1()(key) % _capacity))
return false;
if (!_bitmap.Test(HashFun1()(key) % _capacity))
return false;
if (!_bitmap.Test(HashFun1()(key) % _capacity))
return false;
return true;
}
private:
BitMap _bitmap;
size_t _capacity;
}; 三、布隆过滤器优缺点:
1.优点:
相比于其它的数据结构,布隆过滤器在空间和时间方面都有巨大的优势。布隆过滤器存储空间和插入/查询时间都是常数。另外, Hash 函数相互之间没有关系,方便由硬件并行实现。布隆过滤器不需要存储元素本身,在某些对保密要求非常严格的场合有优势。布隆过滤器可以表示全集,其它任何数据结构都不能;k 和 m 相同,使用同一组 Hash 函数的两个布隆过滤器的交并差运算可以使用位操作进行。
2.缺点
但是布隆过滤器的缺点和优点一样明显。误算率(False Positive)是其中之一。随着存入的元素数量增加,误算率随之增加。但是如果元素数量太少,则使用散列表足矣。另外,一般情况下不能从布隆过滤器中删除元素. 我们很容易想到把位列阵变成整数数组,每插入一个元素相应的计数器加1, 这样删除元素时将计数器减掉就可以了。然而要保证安全的删除元素并非如此简单。首先我们必须保证删除的元素的确在布隆过滤器里面. 这一点单凭这个过滤器是无法保证的。另外计数器回绕也会造成问题。
赐教!