一、二叉排序树
1、定义
二叉排序树(Binary Sort Tree),又称二叉查找树(Binary Search Tree),亦称二叉搜索树。
二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
1、若左子树不空,则左子树上所有节点的值均小于它的根节点的值;
2、若右子树不空,则右子树上所有节点的值均大于它的根节点的值;
3、左、右子树也分别为二叉排序树。
下面的这幅图就是一个二叉排序树
2、二叉排序树的查找
二叉排序树查找在在最坏的情况下,需要的查找时间取决于树的深度:
1、当二叉排序树接近于满二叉树时,其深度为\(log_2n\),因此最坏情况下的查找时间为\(O(log_2n)\),与折半查找是同数量级的。
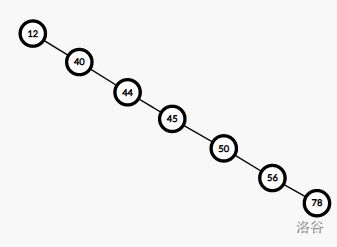
2、但是当二叉树如下图所示形成单枝树时,其深度为\(n\),最坏情况下查找时间为\(O(n)\),与顺序查找属于同一数量级。
所以,为了保证二叉排序树的查找有较高的查找速度,希望该二叉树接近于满二叉树
或者二叉树的每一个节点的左、右子树深度尽量相等
而\(Splay\)可以很好地解决这一问题
二、Splay
伸展树(Splay Tree),也叫分裂树,是一种二叉排序树,它能在\(O(log n)\)内完成插入、查找和删除操作。它由丹尼尔·斯立特Daniel Sleator 和 罗伯特·恩卓·塔扬Robert Endre Tarjan 在1985年发明的。
1、结构体定义
struct trr{
int son,ch[2],fa,cnt,val;
}tr[maxn];
其中\(son\)为儿子数量
\(ch[0]\)为左儿子的编号,\(ch[1]\)为右儿子的编号
\(fa\)为当前节点的父亲节点
\(cnt\)为当前节点的数量
\(val\)为当前节点的权值
2、旋转操作
旋转操作是\(Splay\)中的基本操作
每次有新节点加入、删除或查询时,我们都将其旋转至根节点
这样可以保持\(BST\)的平衡
复杂度证明
我们拿实际的图来演示一下
在这幅图中,\(x\)是\(y\)的左儿子,而我们想要将\(x\)旋转至\(y\)的位置
首先,根据\(BST\)的性质,\(x
因此旋转后,\(y\)应该变为\(x\)的右儿子
那\(x\)原来的右儿子\(b\)呢
根据性质有\(x
\(y\)的右儿子\(c\)和\(x\)的左儿子\(b\)保持不变即可
旋转后的图变成了下面这个样子
旋转后的图仍满足\(BST\)的性质
但实际上,我们只列举出了\(4\)种情况中的一种
1、\(y\)是\(z\)的左儿子,\(x\)是\(y\)的左儿子
2、\(y\)是\(z\)的左儿子,\(x\)是\(y\)的右儿子
3、\(y\)是\(z\)的右儿子,\(x\)是\(y\)的右儿子
4、\(y\)是\(z\)的右儿子,\(x\)是\(y\)的左儿子
如果对于每一种情况我们都分别枚举一遍会很麻烦
根据\(yyb\)神犇的总结
1、\(x\)变到原来\(y\)的位置
2、\(y\)变成了 \(x\)原来在\(y\)的相对 的那个儿子
3、\(y\)的非\(x\)的儿子不变 \(x\)的 \(x\)原来在\(y\)的 那个儿子不变
4、\(x\)的 \(x\)原来在\(y\)的 相对的 那个儿子 变成了 \(y\)原来是 \(x\)的那个儿子
代码如下
void push_up(int x){
tr[x].son=tr[tr[x].ch[0]].son+tr[tr[x].ch[1]].son+tr[x].cnt;
//当前节点儿子数量等于左儿子数量加右儿子数量加当前节点数量
}
void xuanzh(int x){
int y=tr[x].fa;
int z=tr[y].fa;
int k=(tr[y].ch[1]==x);
//判断x是否是y的右儿子
tr[z].ch[tr[z].ch[1]==y]=x;
tr[x].fa=z;//x变到原来y的位置
tr[y].ch[k]=tr[x].ch[k^1];
tr[tr[x].ch[k^1]].fa=y;
//x的原来在x在y的相对位置的那个儿子变成了y原来是x的那个儿子
tr[x].ch[k^1]=y;
tr[y].fa=x;
//y变成了x原来在y的相对的那个儿子
push_up(y);
push_up(x);
//更新节点信息
}
3、将一个节点上旋至规定点
我们是不是对于某一个节点连续进行两次旋转操作就可以呢
一般情况下是可以的,但是如果遇到下面的情况就不可行了
我们要把\(4\)旋转到\(1\)的位置
如果我们一直将\(4\)进行旋转操作,那么旋转两次后的图变成了下面这样
我们会发现\(1-3-5\)这一条链仍然存在
只不过是\(4\)号节点跑到了原来\(1\)号节点的位置
这样的话,\(Spaly\)就失去了意义
因此,我们分情况讨论:
(\(x\)是\(y\)的儿子节点,\(y\)是\(z\)的儿子节点,将\(x\)旋转到\(z\))
1、\(x\)和\(y\)分别是\(y\)和\(z\)的同一个儿子
先旋转\(y\)再旋转\(x\)
2、\(x\)和\(y\)分别是\(y\)和\(z\)不同的儿子
将\(x\)旋转两次
代码
void splay(int x,int goal){
//将x旋转至目标节点goal的儿子
while(tr[x].fa!=goal){
int y=tr[x].fa;
int z=tr[y].fa;
if(z!=goal){
(tr[y].ch[0]==x)^(tr[z].ch[0]==y)?xuanzh(x):xuanzh(y);
}
//分情况讨论:同位置儿子旋转y,不同位置儿子旋转x
xuanzh(x);
//最后旋转x
}
if(goal==0) rt=x;
//如果旋转到根节点,将根节点更新为x
}
4、查找操作
类似于二分查找
从根节点开始,如果要查询的值大于该点的值,向右儿子递归
否则向左儿子递归
如果当前位置的值已经是要查找的数,则将该节点旋转至根节点,方便之后的操作
void zhao(int x){
//查找x的位置,并将其旋转至根节点
int u=rt;
if(!u) return;//树为空
while(tr[u].ch[x>tr[u].val] && x!=tr[u].val){
//当存在儿子并且当前位置的值不等于x
u=tr[u].ch[x>tr[u].val];//跳转到儿子
}
splay(u,0);
//将当前位置旋转到根节点
}
5、插入操作
和查找操作类似,也是从根节点开始
如果要插入的值大于该点的值,向右儿子递归
否则向左儿子递归
如果可以在原树中找到当前值,把节点的数量加一即可
否则再新建一个节点
void ad(int x){
//插入价值为x的节点
int u=rt,fa=0;
while(u && tr[u].val!=x){
fa=u;
u=tr[u].ch[x>tr[u].val];
//向儿子递归
}
if(u) tr[u].cnt++;
//如果当前节点已经存在,节点的个数加一
else {
//如果不存在,建立一个新的节点
u=++tot;
if(fa) tr[fa].ch[x>tr[fa].val]=u;
tr[tot].ch[1]=0;
tr[tot].ch[0]=0;
tr[tot].val=x;
tr[tot].fa=fa;
tr[tot].cnt=1;
tr[tot].son=1;
}
splay(u,0);//将当前节点上旋至根节点
}
6、查询前驱和后继
我们要查询某一个数\(x\)的前驱和后缀
首先我们要使用查找操作,将\(x\)节点旋转到根节点
如果查询前驱,那么前驱就是左子树中权值最大的节点
那我们就从左子树开始,一直向右子树跳,直到没有右子树为止
查询后继也是同样
int qq_hj(int x,int jud){
//jud为0查询前驱,为1查询后缀
zhao(x);
//将x旋转至根节点
int u=rt;
if((tr[u].val>x && jud) || (tr[u].val7、删除操作
如果我们要删除某一个数\(x\)
那么这一个数的权值一定介于它的前驱和它的后继之间
所以我们可以先把它的前驱旋转至根节点
然后把它的后继旋转到它的前驱作为前驱的右儿子
这时,前驱的左儿子恰好比前驱大、后继小,正是我们想要删除的值
void sc(int x){
int qq=qq_hj(x,0);
//求出前驱
int hj=qq_hj(x,1);
//求出后继
splay(qq,0);
//将前驱旋转至根节点
splay(hj,qq);
//将后继旋转至前驱的右儿子
int willsc=tr[hj].ch[0];
//找出要删除的数
if(tr[willsc].cnt>1){
tr[willsc].cnt--;
splay(willsc,0);
} else {
tr[hj].ch[0]=0;
}
//删除该节点
}
8、查找第k小的值
从根节点开始,如果左子树的儿子数大于\(k\),向左子树查询
否则向右子树查询
递归解决问题即可
int kth(int x){
int u=rt;
if(tr[u].sontr[y].son+tr[u].cnt){
x-=(tr[y].son+tr[u].cnt);
u=tr[u].ch[1];
//向右子树查询
} else {
if(x<=tr[y].son) u=y;
else return tr[u].val;
//向左子树查询
}
}
}
练习题(洛谷P3369)
一道很基础的板子题,直接附上代码
#include
using namespace std;
const int maxn=1e6+5;
#define INF 0x3f3f3f3f
struct trr{
int son,ch[2],fa,cnt,val;
}tr[maxn];
int n,tot,rt;
void push_up(int x){
tr[x].son=tr[tr[x].ch[0]].son+tr[tr[x].ch[1]].son+tr[x].cnt;
}
void xuanzh(int x){
int y=tr[x].fa;
int z=tr[y].fa;
int k=(tr[y].ch[1]==x);
tr[z].ch[tr[z].ch[1]==y]=x;
tr[x].fa=z;
tr[y].ch[k]=tr[x].ch[k^1];
tr[tr[x].ch[k^1]].fa=y;
tr[x].ch[k^1]=y;
tr[y].fa=x;
push_up(y);
push_up(x);
}
void splay(int x,int goal){
while(tr[x].fa!=goal){
int y=tr[x].fa;
int z=tr[y].fa;
if(z!=goal){
(tr[y].ch[0]==x)^(tr[z].ch[0]==y)?xuanzh(x):xuanzh(y);
}
xuanzh(x);
}
if(goal==0) rt=x;
}
void zhao(int x){
int u=rt;
if(!u) return;
while(tr[u].ch[x>tr[u].val] && x!=tr[u].val){
u=tr[u].ch[x>tr[u].val];
}
splay(u,0);
}
void ad(int x){
int u=rt,fa=0;
while(u && tr[u].val!=x){
fa=u;
u=tr[u].ch[x>tr[u].val];
}
if(u) tr[u].cnt++;
else {
u=++tot;
if(fa) tr[fa].ch[x>tr[fa].val]=u;
tr[tot].ch[1]=0;
tr[tot].ch[0]=0;
tr[tot].val=x;
tr[tot].fa=fa;
tr[tot].cnt=1;
tr[tot].son=1;
}
splay(u,0);
}
int qq_hj(int x,int jud){
zhao(x);
int u=rt;
if((tr[u].val>x && jud) || (tr[u].val1){
tr[willsc].cnt--;
splay(willsc,0);
} else {
tr[hj].ch[0]=0;
}
}
int kth(int x){
int u=rt;
if(tr[u].sontr[y].son+tr[u].cnt){
x-=(tr[y].son+tr[u].cnt);
u=tr[u].ch[1];
} else {
if(x<=tr[y].son) u=y;
else return tr[u].val;
}
}
}
int main(){
int n;
scanf("%d",&n);
ad(INF);
ad(-INF);
for(int i=1;i<=n;i++){
int aa,bb;
scanf("%d%d",&aa,&bb);
if(aa==1) ad(bb);
else if(aa==2) sc(bb);
else if(aa==3) {
zhao(bb);
int ans=tr[tr[rt].ch[0]].son;
printf("%d\n",ans);
} else if(aa==4){
int ans=kth(bb+1);
printf("%d\n",ans);
} else if(aa==5){
int ans=qq_hj(bb,0);
printf("%d\n",tr[ans].val);
} else {
int ans=qq_hj(bb,1);
printf("%d\n",tr[ans].val);
}
}
return 0;
}