有价值的题目:4,8,9,10,11,12,13,14,15,16
例7【2019届高三理科数学二轮用题】若二项式\((x-\cfrac{1}{\sqrt{x}})^n\)的展开式中第\(m\)项为常数项,则\(m\),\(n\)应该满足【】
分析:由于\((a+b)^n\)的二项展开式的通项公式为\(T_{r+1}=C_n^r\cdot a^{n-r}\cdot b^r\),
故\(T_{r+1}=C_n^r\cdot x^{n-r}\cdot (-\cfrac{1}{\sqrt{x}})^r=(-1)^r\cdot C_n^r\cdot x^{n-\cfrac{3r}{2}}\),
则\(n-\cfrac{3r}{2}=0\),且\(m=r+1\),代入整理得到,\(2n=3(m-1)\),故选\(A\)。
例8【2019届高三理科数学二轮用题】已知一只蚂蚁在底面半径为5cm,高为12cm的圆锥侧面爬行,若蚂蚁在圆锥侧面上任意一点出现的可能性相等,且将蚂蚁看作一个点,则蚂蚁距离圆锥顶点超过5cm的概率为【】
分析:将题目中的圆锥展开后,则其侧面形成一个半径为\(13\),弧长为\(10\pi\)的扇形,如下图所示,
要使的蚂蚁距离圆锥顶点超过5cm,则蚂蚁应该在扇环内部,而小扇形的弧长可以这样计算\(\cfrac{l}{5}=\cfrac{10\pi}{13}\),故小扇形的弧长为\(\cfrac{50\pi}{13}\),
故所求概率为\(P=1-\cfrac{\cfrac{1}{2}\times \cfrac{50\pi}{13}\times 5}{\cfrac{1}{2}\times 10\pi\times 13}=\cfrac{144}{169}\),故选\(C\)。
例9【2019届高三理科数学二轮用题】已知数列\(\{a_n\}\)满足\(t\cdot S_n=n^2-12n\),其中\(S_n\)为数列\(\{a_n\}\)的前\(n\)项和,若\(a_1+a_3+a_5=42\),\(a_2+a_4=28\),则当\(S_n\)取最大值时,\(n=\)【】
分析:简单记录思路,由\(a_n\)与\(S_n\)的关系先求得\(a_n=\cfrac{2n-13}{t}\),利用\(a_2+a_4=28\),求得\(t=-\cfrac{1}{2}\),
这样\(a_n=26-4n\),令\(a_n>0\),解得\(n\leq 6\),由邻项变号法可知,\(S_6\)最大,故选\(B\)。
例10【2019届高三理科数学二轮用题】在矩形\(ABCD\)中,\(AB=2\),\(AD=4\),\(AC\)与\(BD\)相交于点\(O\),过点\(A\)作\(AE\perp BD\)于\(E\),则\(\overrightarrow{AE}\cdot \overrightarrow{AC}\)=【】
法1:从形的角度思考,采用坐标法求解;以点\(A\)为坐标原点建立如图所示的直角坐标系,
则可知\(A(0,0)\),\(B(0,-2)\),\(C(4,-2)\),\(D(4,0)\),设\(E(x,y)\),
则由\(k_{AE}\cdot k_{BD}=-1\),可得\(y=-2x\)①,又直线\(BD:2y=x-4\)②,
联立①②可得,\(x=\cfrac{4}{5}\),\(y=-\cfrac{8}{5}\),
则\(\overrightarrow{AE}\cdot \overrightarrow{AC}=(\cfrac{4}{5},-\cfrac{8}{5})\cdot (4,-2)=\cfrac{32}{5}\),故选\(C\).
法2:本题目是否还可以用基向量法,以\(\overrightarrow{AB}\)和\(\overrightarrow{AD}\)为基向量来表示其他向量,待思考;
例11【2019届高三理科数学二轮用题】已知抛物线\(C:y^2=ax(a>0)\),若直线\(l:y=4x-a\)被抛物线\(C\)截得的弦长为\(17\),则与抛物线\(C\)相切且平行于直线\(l\)的直线方程为【】
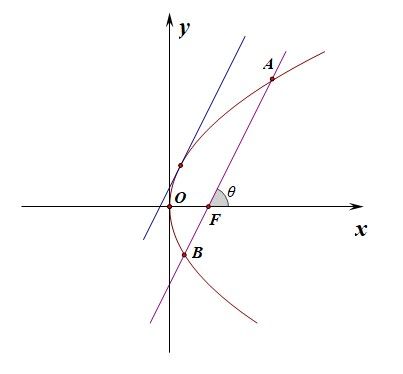
分析:如图所示,直线过抛物线的焦点,故利用抛物线的焦点弦长公式可得,\(\cfrac{2p}{sin^2\theta}=17\),
又由于直线的斜率\(k=4\),则\(sin^2\theta=\cfrac{2p}{17}\),\(cos^2\theta=\cfrac{17-2p}{17}\),则\(k^2=16=tan^2\theta=\cfrac{2p}{17-2p}\),
解得\(p=8\),从而\(a=16\),抛物线为\(y^2=16\);
由图可知所求直线和抛物线相切于第一象限,故涉及到的函数为\(y=f(x)=4\sqrt{x}\),
设切点为\(P(x_0,y_0)\),则\(f'(x_0)=\cfrac{2}{\sqrt{x_0}}=4\),求得\(x_0=\cfrac{1}{4}\),\(y_0=2\),
又所求直线的\(k=4\),由点斜式方程可得,所求直线为\(4x-y+1=0\),故选\(B\).
解后反思:焦点弦的公式不止一个,此处选用这一个就是考虑变量少,运算简单。
例12【2019届高三理科数学二轮用题】已知函数\(f(x)=mx-\cfrac{1-m}{x}+lnx\),要使得函数\(f(x)>0\)恒成立,则正实数\(m\)应该满足【】
法1:先考虑分离参数法,若能成功分离参数,那么得到的形式必然是\(m>g(x)\)或\(m
法2:由函数\(f(x)>0\)恒成立,则需要求在\((0,+\infty)\)上的函数\(f(x)_{min}>0\)即可,故考虑用导数方法;
\(f'(x)=\cfrac{(x+1)[mx+(1-m)]}{x^2}\), 故函数在\(x=\cfrac{m-1}{m}\)处取到最小值,则要使得函数\(f(x)>0\)恒成立,只需要\(f(\cfrac{m-1}{m})>0\)即可,
对此化简整理得到,正实数\(m\)应该满足\(\cfrac{m-1}{m}\cdot e^{2m-1}>1\),故选\(C\)。
解后反思:本题目的解法有点漏洞,条件中应该使得\(m>1\),而不仅仅是\(m>0\),否则当\(0
例13【2019届高三理科数学二轮用题】已知不等式组\(\left\{\begin{array}{l}{2x-y\ge 0}\\{2-2y\leq 0}\\{x\leq 2}\end{array}\right.\)所表示的区域为\(\Omega\),则区域\(\Omega\)的外接圆的面积为__________.
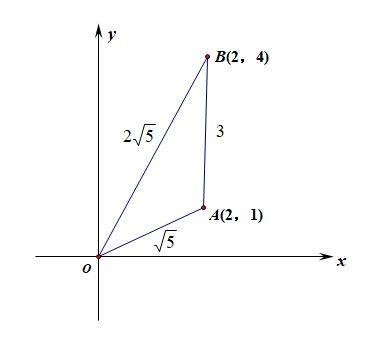
分析:做出如图所示的三角形可行域,三条边长可知,故求其外接圆的半径可以采用\(S_{\triangle OAB}=\cfrac{abc}{4R}\),
又由于\(S_{\triangle OAB}=\cfrac{1}{2}\times 3\times 2=3\),则\(3=\cfrac{3\times \sqrt{5}\times 2\sqrt{5}}{4R}\),解得\(R=\cfrac{5}{2}\),故\(S_{外接圆}=\cfrac{25\pi}{4}\)。
解后反思:结合题目的具体条件,选择恰当的公式,计算量能相应的减少。
例14【2019届高三理科数学二轮用题】已知函数\(f(x)=-x^3+mx+2\),\(g(x)=2x^2-nx\),且曲线\(y=f(x)\)在点\((2,f(2))\)处的切线于曲线\(y=g(x)\)在点\((1,g(1))\)处的切线平行,则\(\sqrt{m^2+n^2}\)的最小值为_______。
法1:由已知条件可知,\(m+n=16\),若从数的角度入手分析,则\(m=16-n\),
转化为先求\(m^2+n^2=(16-n)^2+n^2=2n^2-32n+16^2=2(n-8)^2+128\),
故\((m^2+n^2)_{min}=128\),故所求最小值为\(\sqrt{128}=8\sqrt{2}\)。
法2:由已知条件可知,\(m+n=16\),若从形的角度入手分析,建立如图所示的坐标系,
可知,\(m+n=16\)表示一条直线,\(\sqrt{m^2+n^2}=\sqrt{(m-0)^2+(n-0)^2}\)表示定点\((0,0)\)与动点\((m,n)\)的距离,
故所求的最小距离为\(8\sqrt{2}\)。
例15【2019届高三理科数学二轮用题】已知\(F_1\),\(F_2\)分别是双曲线\(C:\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2}=1\) \((a>0,b>0)\)的左右焦点,以\(F_2\)为圆心做一个圆,使该圆过线段\(OF_2\)的中点,若该圆与双曲线的两条渐近线有公共点,则双曲线\(C\)的离心率的取值范围是___________。
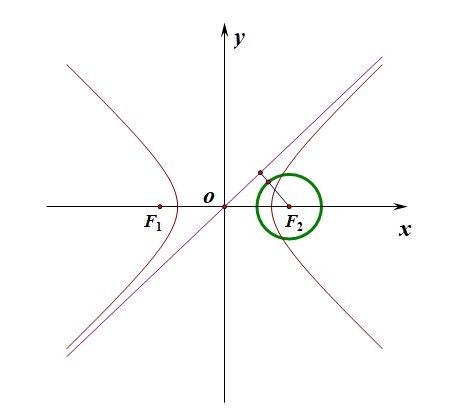
分析:如下图所示,可知圆\(F_2\)的圆心为\(F_2(c,0)\),半径为\(r=\cfrac{c}{2}\),由于圆和双曲线都关于坐标轴对称,故只需要保证圆和一条渐近线\(y=\cfrac{b}{a}x\)有公共点即可,
此时可以使用联立直线方程和双曲线的方程,使用\(\Delta \ge 0\)的思路,也可以利用圆心到直线的距离小于半径的思路,很明显第二个思路的运算量要小一些。
此时圆心为\(F_2(c,0)\),半径为\(r=\cfrac{c}{2}\),直线为\(bx-ay=0\),故\(d=\cfrac{|bc-a\times 0|}{\sqrt{a^2+b^2}}\leq \cfrac{c}{2}\),
化简整理得到,\(2b\leq c\),即\(4b^2\leq c^2\),则\(4c^2-4a^2\leq c^2\),整理为\(\cfrac{c^2}{a^2}\leq \cfrac{4}{3}\),故\(e\leq \cfrac{2\sqrt{3}}{3}\),又双曲线的\(e>1\),故\(e\in (1,\cfrac{2\sqrt{3}}{3}]\).
例16【2019届高三理科数学二轮用题】在面积为4的正方形\(ABCD\)中,\(M\)是线段\(AB\)的中点,现将图形沿\(MC\),\(MD\)折起,使线段\(MA\)和\(MB\)重合,得到一个四面体\(A-CDM\),其中点\(B\)和点\(A\)重合,则该四面体外接球的表面积为_________。
分析:平面图形如左图,立体图形如右图所示,\(\angle MAC=\angle MAD=\cfrac{\pi}{2}\),下来的重点是如何将四面体放置在球体内部。
![]()
可以这样来思考,将最特殊的面\(ACD\)放置在下底面,这样方便来放置和下底面垂直的侧棱,如下图所示;
![]()
底面圆的圆心\(O'\)为下底面正三角形的重心,\(O\)为球心,则\(OA=OM=R\),由于\(\triangle ACD\)为等边三角形,\(AC=2\),则\(CH=1\),\(AH=\sqrt{3}\),则\(AO'=\cfrac{2\sqrt{3}}{3}\),过点\(O\)做\(OK\perp AM\)于\(K\),则\(OK=AO'=\cfrac{2\sqrt{3}}{3}\),又\(AK=\cfrac{1}{2}AM=\cfrac{1}{2}\),在\(Rt\triangle AOK\)中,由勾股定理可知\(R^2=(\cfrac{2\sqrt{3}}{3})^2+(\cfrac{1}{2})^2=\cfrac{19}{12}\),故\(S_{球O}=4\pi R^2=\cfrac{19\pi}{3}\)。
补充说明:如果想不清这一点,还可以想着将四面体补体成一个直三棱柱,如下图的动图所示,
解后反思:当一条侧棱和下底面垂直时,常将三棱锥\(M-ACD\)补体成直三棱柱\(MC'D'-ACD\),这样容易想清楚。