2019独角兽企业重金招聘Python工程师标准>>> ![]()
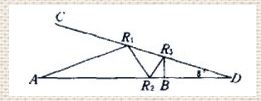
1、如图所示,从A点发出一束激光,于AD直线和CD直线反射多次后,垂直达到了B点(B点可能在AD上也可能在CD上,入射角等于反射角),如角CDA=8°,那么最多反射次数是____。(从B点原路反射回点A次数不纳入计算,图中给出3次反射的例子)
答案:10
解析:光学物理,几何及数列,从B原路返回计算,B的入射角记为a0 = 0度,R3的入射角记为a1=8度,R2的入射角a2记为a2,第n个入射角记为an。则有a0=0; a1=8; a(n+1)=2an-a(n-1)。可得an=8n。入射角an<90,则n最大为11,而入射点A点在边缘上,所以只有10次。望斧正。
如果入射光平行与角的边,那么会没有反射。
如果入射光和面稍微有一点夹角,此时应该是反射次数最多的情况。
如果入射光垂直与边时,势必入射角为90-8=82度。
而每次入射角大小比上一次入射角大8度,
那么此时 反射此时最多为82/8=10次
2、假定CSomething是一个类,执行下面这些语句之后,内存里创建了____个CSomething对象。
| 1 2 3 4 5 6 7 |
CSomething a(); CSomething b(2); CSomething c[3]; CSomething &ra = b; CSomething d=b; CSomething *pA = c; CSomething *p = new CSomething(4); |
答案:6个
解析:
CSomething a(); 只是个函数声明
CSomething b(2); +1
CSomething c[3]; +3,对象数组
CSomething &ra = b; 引用,没有新构造
CSomething d=b; +1,调用拷贝构造函数
CSomething *pA = c; 只是给指针赋值
CSomething *p = new CSomething(4); +1,构造并给指针赋值
总共6个
去掉括号才是声明一个CSomething对象,调用默认构造函数。它有括号却没有参数,所以不是调用有参数的构造函数。所以只是一个声明了一个输入为void,输出为CSomething类型的函数。 反过来想可以更顺一些,若要声明一个这样的参数该怎么写,就很容易想明白了
3、假设淘宝网上某商品A在任一时刻t内若有人浏览,则该商品在下一时刻t+1内无人浏览的概率为0.35(即下一时刻的浏览情况仅与当前时段相关),定义此条件概率为 P(O_{t+1}=0|O_t=1)=0.35(即用“1”代表有人浏览的事件,用“0”代表无人浏览的事件),类似得定义P(O_{t+1}=1|O_t=1)=0.65,P(O_{t+1}=0|O_t=0)=0.4,P(O_{t+1}=1|O_t=0)=0.6。若此商品A在t=0时有人浏览,它在t=100000时有人浏览的概率是____。
答案:0.6316
解析:
4、猜数字游戏的过程是你输入一个4位数(数字选取0~9,不会重复),电脑会告诉你两个信息:A个数字和位置均正确,B个数字正确但位置错误。例如正确答案是7890你输入0789,电脑会告诉你0A4B,表示有0个数字和位置完全正确,但有4个数字正确但位置错误。现在牛妹猜了三次的结果分别是:1234=>0A4B,2341=>1A3B,3412=>2A2B,那么牛妹最少还要猜____次才能保证一定得到4A0B的结果。
答案:3
解析:
分析后的结果只可能是2413、4312、3142、3421,那么我们接下来肯定要从这几个数里面猜。
假设最后的结果是3421。
(1) 我们先猜2413,会提示1A,那么就可以排除结果是3142的可能(如果是,2413会提示0A),只可能是4312和3412,那么我们猜2次或者3次就可以得到正确结果;
(2) 如果我们先猜4312,会提示0A,那么就可以排除2413和3142,只剩下3421,这样我们只需猜2次就可以确定。
(3) 如果我们先猜3142,会提示1A,那么就可以排除2413,这样我们只需猜2次或3次就可以确定。
(4) 如果我们先猜3421,会提示4A,这样我们只需猜1次就可以确定。
综上,我们要猜结果是3421,至少要猜3次就一定能保证。
同理,猜结果是2413、4312、3142也一样。
5、对一棵二叉树进行后续遍历,其输出结果为A,B,C,这样的二叉树有____棵。
答案:5
6、下面数据结构能够支持随机的插入和删除操作、并具有较好的性能的是____。
答案:链表和哈希表
7、有一个类A,其数据成员如下:
class A {
...
private:
int a;
public:
const int b;
float* &c;
static const char* d;
static double* e;
};则构造函数中,成员变量一定要通过初始化列表来初始化的是:______。
答案:b,c
构造函数中,成员变量一定要通过初始化列表来初始化的有以下几种情况:
1、const常量成员,因为常量只能在初始化,不能赋值,所以必须放在初始化列表中;
2、引用类型,引用必须在定义的时候初始化,并且不能重新赋值,所以也要写在初始化列表中;
3、没有默认构造函数的类类型,因为使用初始化列表可以不必调用默认构造函数来初始化,而是直接调用拷贝构造函数;
初始化:从无到有,创建了新对象;如:string foo = "Hello World!"
赋值:没有创建新对象,而是对已有对象赋值。 如:string bar; bar = "Hello World!"
有时我们可以忽略数据成员初始化和赋值之间的差异,但并非总能这样。
如果成员是const或者是引用的话,必须将其初始化。类似的,当成员属于某种类类型且该类没有定义默认构造函数时,也必须将这个成员初始化。(比如:类A中有一成员是B b,但类B中没有定义默认构造函数时,就必须对A中b成员进行初始化)
随着构造函数体一开始执行(即大括号里面部分),初始化就完成了(构造函数体内只是赋值操作)。因此,上面三种情况,比如初始化const或者引用类型的数据成员的唯一机会就是通过构造函数初始值,形如:ConstRef::ConstRef(int n) : i(n), j(n) { }
8、在如下8*6的矩阵中,请计算从A移动到B一共有____种走法。要求每次只能向上或向右移动一格,并且不能经过P。
答案:492
解析:
8*6的矩阵,从左下角A到右上角B,一共需要走12步,其中5步向上,7步向右,因此总的走法一共有C(12,5)=792种,但题目规定不能经过P,因此需要减去经过P点的走法。
经过P的路径分为两部分,从A到P,从P到B。
同理,从A到P的走法:C(6,2)=15;
同理,从P到B的走法:C(6,3)=20;
因此从A到B经过P点的走法有15*20=300种,
所以从A到B不经过P点的走法有792-300=492种。
C(12,5)=(12*11*10*9*8)/ (5*4*3*2*1)
9、一个英雄基础攻击力为100,携带了三件暴击武器,武器A有40%的概率打出2倍攻击,武器B有20%的概率打出4倍攻击,武器C有10%概率打出6倍攻击,各暴击效果触发是独立事件,但是多个暴击效果在一次攻击中同时触发时只有后面武器的暴击真正生效,例如一次攻击中武器A判定不暴击,武器B和武器C都判定触发暴击,那么这次攻击实际是600攻击力。那么这个英雄攻击力的数学期望是____。
答案:232.8
解析
(600 * 10%) // 使用武器C
+(400* 90% * 20% ) // 使用武器B,需要保证没有使用武器C,否则因为多个暴击效果在一次攻击中同时触发时只有后面武器的暴击真正生效,武器B不生效
+(200 * 90% * 80% * 40%) // 同理,使用武器A,需要保证武器B和C都没有使用
+(100*60%*80%*90%)// 没有使用任何武器
= 232.8
10、以下函数中,和其他函数不属于一类的是____。
fwrite
putc
pwrite
putchar
getline
scanf
答案:pwrite
解析:
C,pwrite是系统调用,其他都是库函数
常见文件系统 系统函数
- fcntl 文件控制
- open 打开文件
- creat 创建新文件
- close 关闭文件描述字
- read 读文件
- write 写文件
- readv 从文件读入数据到缓冲数组中
- writev 将缓冲数组里的数据写入文件
- pread 对文件随机读
- pwrite 对文件随机写
Linux下对文件操作有两种方式:系统调用(system call)和库函数调用(Library functions)。系统调用实际上就是指最底层的一个调用,在linux程序设计里面就是底层调用的意思。面向的是硬件。而库函数调用则面向的是应用开发的,相当于应用程序的api。
简明的回答是:函数库调用是语言或应用程序的一部分,而系统调用是操作系统的一部分。
11、某操作系统采用分页存储管理方式,下图给出了进程A和进程B的页表结构。如果物理页的大小为512字节,那么进程A与进程B的物理内存总共使用了____字节。
进程A页表: 进程B页表:
逻辑页 物理页 逻辑页 物理页
0 9 0 1
1 2 1 3
2 4 2 4
3 6 3 7
4 4 2
5 5
答案:3584
解析:
物理页可以在进程间共享,两个进程共使用了1,2,3,4,6,7,9,共7个物理页。
故:7*512=3584
12、现有1G数据需要排序,计算资源只有1G内存可用,下列排序方法中最可能出现性能问题的是____。
堆排序
插入排序
归并排序
快速排序
选择排序
冒泡排序
答案:归并排序
解析:
13、凯撒(Caesar)密码是一种基于字符替换的对称式加密方法,它是通过对26个英文字母循环移位和替换来进行编码的。设待加密的消息为"Alibaba Group",加密后的密文是"RCzsrsr XIFLG",则采用的密匙k是____。
答案:17
解析:本题的突破口是子串“baba“对应子串”srsr”,b和s、a和r之间相差17,我们就可以猜测k=17。然后对剩下的对应元素一一进行验证,验证的结果发现是正确的,其实就相当于我们对a~z,A~Z依次编号为1~26,27~52
14、有1,2,3,......无穷个格子,你从1号格子出发,每次1/2概率向前跳一格,1/2概率向前跳两格,走到格子编号为4的倍数时结束,结束时期望走的步数为____。
答案:3.6
解析:还是设f(i)表示在第i号格子上时,期望再走多少步结束。
则从1号开始走,我们的目标是求f(1)
f(1) = 0.5 * ( 1 + f(2) ) + 0.5 * ( 1 + f(3) ) 即有0.5概率走一步到2号,0.5概率走两步到3号
f(2) = 0.5 * ( 1 + f(3) ) + 0.5 * ( 1 + f(4) ) 即有0.5概率走一步到3号,0.5概率走两步到4号(结束)
f(3) = 0.5 * ( 1 + f(4) ) + 0.5 * ( 1 + f(1) ) 即有0.5概率走一步到4号,0.5概率走两步到5号(5号即可看做1号)
f(4) = 0 走到4号就结束了,故为0
可以解上述方程,得f(1) = 18/5.
15、从1,2,3,......,49,50里选择一个集合S,使得若x属于S,则2x不属于S,则S最多能有____个元素。
答案:33
解析:首先选出26-50共25个数,肯定不会有他们的二倍的数在集合中.同时可以去掉13-25,因为他们的二倍全在26-50中.
剩下1-12.此时类似原问题,选择7-12共6个数(他们的二倍已经被去掉了).同时去掉4-6,也因为他们的二倍都在7-12中.
最后可以选择1,3两个数.
这样总共有25+6+2=33个
16、Linux下两个进程可以同时打开同一个文件,这时如下描述错误的是:
A、两个进程中分别产生生成两个独立的fd
B、两个进程可以任意对文件进行读写操作,操作系统并不保证写的原子性
C、进程可以通过系统调用对文件加锁,从而实现对文件内容的保护0
D、任何一个进程删除该文件时,另外一个进程会立即出现读写失败
E、两个进程可以分别读取文件的不同部分而不会相互影响
F、一个进程对文件长度和内容的修改另外一个进程可以立即感知
答案:D、任何一个进程删除该文件时,另外一个进程会立即出现读写失败
解析:应该选D, 一般删除都是文件索引,如果两个文件同时打开同一个文件,一个线程执行删除操作,只要另一个线程不退出,就可以继续对该文件进行操作,一旦退出才找不到该文件的索引节点而报错。
17、考虑以下二分查找的代码:
#include
int bsearch(int array[], int n, int v)
{
int left, right, middle;
left = 0, right = n - 1;
while (left <= right) {
middle = left + (right - left) / 2;
if (array[middle] > v ) {
right = middle;
} else if (array[middle] < v) {
left = middle;
} else {
return middle;
}
}
return -1;
} 对于输入array为:{2, 6, 8, 10, 13, 25, 36, 45, 53, 76, 88, 100, 127}, n = 13, v = 127时,
运行bsearch函数,while循环调用的次数为____。
答案:无数次
解析:第一次middle=6,第二次middle=9,第三次middle=10,第四次middle=11,之后由于middle=11+(12-11)/2=11,一直没有变化所以为无数次
要注意:中间有个坑,right = middle - 1; left = middle + 1时才是真正的二分搜索法。
18、在一个axb的整数矩阵中,寻找最长的严格递减数字序列。数列可以沿着横或竖的方向,但不能重叠,该问题的最优复杂度是____。举例来说,以下是一个3x5的矩阵,其结果如下:
答案:O(M*N)
解析:动态规划+记忆化可以O(MN)
int dfs(x, y) { //从(x,y) 开始递减最长长度
if (f[x][y] != 0) return f[x][y]; //已经计算过的直接return答案 O(1)
f[x][y]=1;
for (4 个方向) {
if (a[x][y] > a[xx][yy]) f[x][y]=max(f[x][y], dfs(xx, yy) + 1);
}
return f[x][y];
}
void main() {
memset(f, 0, sizeof(f));
for (int i = 1; i <= n; ++i) for (int j = 1; j <= m; ++j) {
ans = max(ans, dfs(i, j));
}
}
虽然有两层for循环,但有些dfs(i,j)是O(1)的。每个点只被遍历一次后就记录下f[x][y]。
所以是O(M*N) + O(M*N) //dfs()总的复杂度+两层for的复杂度
19、设一棵二叉树有 3 个叶子节点,有 8 个度为 1 的节点,则该二叉树中总的节点数为______。
答案:13
解析:设度为0,为1,为2的节点分别有N0,N1,N2.则有以下等式
N0+N1+N2=1*N1+2*N2+1
解方程,得 N0=N2+1,题中说N0=3,则N2=2;
故N0+N1+N2=2+3+8=13
20、一台机器对200个单词进行排序花了200秒(使用冒泡排序),那么花费800秒,大概可以对多少个单词进行排序
答案:400
解析:
n的数据量,时间复杂度是O(n^2),200单词是200秒
2n的数据量时间复杂度是2^2O(n),400单词是800秒
答案应该是400个单词