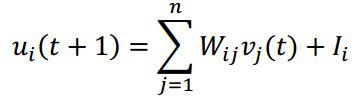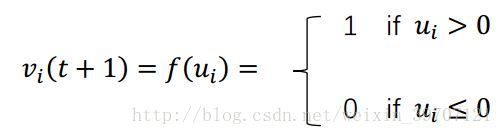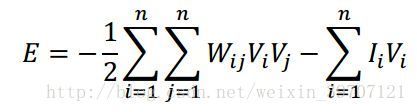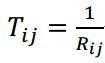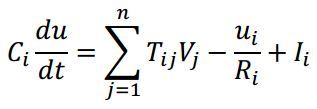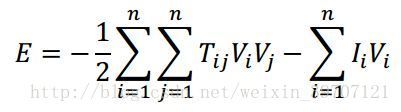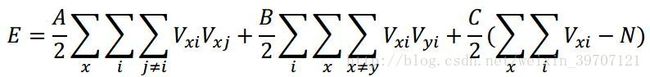Hopfield神经网络

 摘要：

       从系统观点看，前馈神经网络模型的计算能力有限，具有自身的一些缺点。而反馈型神经网络是一种反馈动力学系统，比前馈神经网络拥有更强的计算能力，可以通过反馈而加强全局稳定性。反向传播神经网络模型虽然很适合处理学习问题，但是却不适合处理组合优化问题。理论上来说，如果参数设置得当，Hopfield神经网络可以被用来优化任何问题。反馈神经网络中，所有神经元具有相同的地位，没有层次差别。它们之间可以互相连接，也可向自身反馈信号。典型的反馈性神经网络包括Hopfield神经网络和BAM双向联想记忆神经网络。

       Hofield论文可读性好，他将一些重要的思想结合起来并进行了简要的数学分析（包括Lyapunov稳定性定理的应用）。他指出了神经网络与统计物理学中磁性材料的Ising模型的相似之处。这使得许多已存在的理论可用来对神经网络进行分析，同时也鼓舞了许多科学家和工程师开始注意对神经网络的研究。贝尔实验室早在1987年就成功在Hopfield网络的基础上研制出了神经网络芯片，Hopfield网络一个主要的应用前景是在与VLSI和光学设备的并行实现。Hopfield强调实现，不仅体现在他网络的实现上，也体现在这些网络所解决的问题上。他早期论文描述的应用包括按内容寻址存储器，模数转换及优化问题。可以用它实现A/D转换和解决优化组合计算等问题，如具有代表意义的TSP问题，1985年Hopfield和Tank用Hopfield网络求解N=30的TSP问题，使用900个神经元组成的网络在0.2秒时间内找到一个次优解（在10的30次个可能的解中排除10的23次幂个非最优解），从而创建了神经网络优化的新途径。Hopfield在网络中引入了能量函数的概念，利用Lyapunov稳定性概念证明了当连接权矩阵为对称的情况下，网络在平衡点附近是稳定的，这在神经网络研究领域成为一个重要的里程碑。

下面正式介绍网络结构：

上图为Hopfield神经网络结构图。

      首先，网络结构上，Hopfield神经网络是一种单层互相全连接的反馈型神经网络。每个神经元既是输入也是输出，网络中的每一个神经元都将自己的输出通过连接权传送给所有其它神经元，同时又都接收所有其它神经元传递过来的信息。即：网络中的神经元在t时刻的输出状态实际上间接地与自己t-1时刻的输出状态有关。神经元之间互连接，所以得到的权重矩阵将是对称矩阵。

       同时，Hopfield神经网络成功引入能量函数的概念，使网络运行地稳定性判断有了可靠依据。基本的Hopfield神经网络是一个由非线性元件构成的全连接型单层递归系统。其状态变化可以用差分方程来表示。递归型网络的一个重要特点就是它具有稳定状态‘当网络达到稳定状态的时候，也就是它的能量函数达到最小的时候。这里的能量函数不是物理意义上的能量函数，而是在表达形式上与物理意义上的能量概念一致，即它表征网络状态的变化趋势，并可以依据Hopfield网络模型的工作运行规则不断地进行状态变化，最终能够到达具有某个极小值的目标函数。网络收敛就是指能量函数达到极小值。

       如果把一个最优化在着递归信号，网络的状态是随时间的变化而变化的，其运动轨迹必然存在着稳定性的问题。这就是递归网络与前向网络在网络性能分析上最大的区别之一在使用递归网络时，必须对其稳定性进行专门的分析与讨论，合理选择网络的参数变化范围，才能确保递归网络的正常工作。

       Hopfield神经网络模型有离散型和连续性两种，离散型适用于联想记忆，连续性适合处理优化问题。

离散型Hopfield神经网络：

       离散随机Hopfield神经网络：每个神经元只取二元的离散值0、1或-1、1。神经元i和神经元j之间的权重由 决定。神经元有当前状态和输出。虽然可以使连续值，但在离散模型中是二值的。神经元状态和输出的关系如下，也就是离散型Hopfield神经网络演化方程：

       其中 是神经元i的外部连续输入，f()是激活函数。用于联想记忆时训练完成后权重是不变的，网络中可变的参数只有一直在更新的神经元状态和神经元输出。由于神经元随机更新，所以称此模型为离散随机型。当网络更新时，如果权重矩阵与非负对角线对称，则下面这个能量函数可以保证最小化，直到系统收敛到其稳定状态之一。

      此离散随机型模型中，神经元状态方程对能量函数执行梯度下降。如果权重和偏置被适当地固定，这个过程可以用来最小化任何二元变量的二次函数。

      离散型Hopfield神经网络适合处理联想记忆问题

       离散型Hopfield神经网络适合处理联想记忆问题，这个联想记忆是什么嘞？

       如上图这个例子，这就是离散型Hopfield网络的工作方式。我们以T这个字母为例，首先生成一张完整的T字形图片，然后将图片映射到神经网络中的每个神经元，即每个像素都对应网络中的一个神经元，T字上的像素映射到网络上的神经元，对应值是1（激活状态），T字外的像素映射到网络上的神经元，对应值为0（抑制状态）。然后进行训练，训练的过程是保持神经元状态不变，通过修改权值，使得当神经元的状态和T字形正好对应的同时，网络的能量函数

        正好到达最低点（关于具体训练过程以及能量函数的书写问题请看后面关于联想记忆、TSP问题、snake_hopfield问题的博文）。训练完成后，网络便存储T这个模式。这样，如果在网络中再输入右图这种加入噪声、只有一半的T字图片（输入过程还是和训练一样，将像素点映射到神经元上），经过网络迭代，不断修改神经元的状态，能量函数到达训练时的最低点时，神经元的状态最终便会变成完整的T字形。训练过程实际就是：由于能量函数是有界的，所以系统最后必趋于稳定状态，并对应于在状态空间的某一局部极小值。适当地选取初始状态，网络状态最终将演化到初始状态附近的极小值。如果存储的模式正好对应于该极小值，则意味着当输入与存储样本相似时，会联想起极小值处的储存样本，所以Hopfield神经网络具有联想记忆功能。

      神经网络能够用于大规模信息处理系统，主要是因为神经网络的动力学行为具有稳定的吸引子。网络的状态向稳定点的运动可以理解为由一个不完整的输入模式向完整模式的演化过程，因而模拟了联想记忆中的信息储存机制。概括的说，神经网络的非线性动力学行为模拟了联想和信息处理过程，这是神经网络用于联想记忆的理论基础。

      离散型Hopfield神经网络的联想记忆实质是：将要存储的记忆样本用矢量表示；神经网络在输入记忆样本后，经过演化最终稳定在记忆样本上；当神经网络的输入为非线性记忆样本时，网络输出应该要么稳定于记忆样本，要么稳定于稳定的非线性样本；不论外部输入为何，神经网络的输出应该是稳定的。

连续性Hopfield神经网络：

      在生物系统中，由于神经元i的细胞膜输入电容 、跨膜电阻和确定阻抗，状态会滞后于其它神经元的瞬时输出。神经元的输出将是0、1之间的连续值，而不是之前离散模型的二值。在这个模型中，使用如下的电阻电容微分方程来决定的更新速率，因此可以得到如下的连续型Hopfield神经网络。

连续性Hopfield神经网络中，组成电路的基本器件为：

（1）带有同向和反向输出端的运算放大器，且具有饱和非线性特性的S型输入输出关系，即：

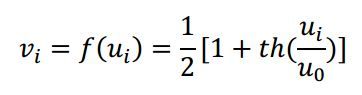
其中相当于输入信号的放大倍数，也控制激活函数的斜率，当趋近于0时，f就成为二值阈值函数。

（2）放大器的输入电容 和输入电阻的乘积为神经元的时间常数，描述了神经元的动态特性。

（3） 代表网络神经元连接的权值，为连接电阻。

（4）外加偏置电流 相当于神经元的阈值，整个电路系统的动态方程为

      若这个方程有解，则表示系统状态变化最终会趋于稳定。在对称连接和无自反馈的情况下，定义系统的能量函数为

     稳态时，可忽略最后的积分项得到

      当非线性作用函数 是连续的单调递增函数时，可以证明能量函数E是单调递减且有界的，即。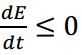

       连续型Hopfield神经网络解决组合优化问题：Hopfield和Tank意识到，用这种基本的神经网络组织形式，选择好能够恰当表示要被最小化的函数和期望的状态的权重和外部输入，便可以计算出解决特定优化问题的方法。根据微分方程来更新神经元确保了能量函数和优化问题可以同时被最小化。神经元的模拟性质和更新过程的硬件实现可以结合起来，创建一个快速而强大的解决方案。用神经网络解决各种组合优化问题时的关键是把问题映射为一神经网络动力系统，并写出相应的能量函数表达式和动力学方程，他们应满足问题的约束条件；最后研究神经网络的动力学过程，以保证网络的稳态输出与能量函数的极小值和组合优化问题的解相对应。

      使用Hopfield神经网络解决TSP问题时，就相当于将需要最小化的目标函数和作为惩罚项的约束共同组成能量函数方程。

连续型Hopfield神经网络解决TSP问题：

TSP问题简介：

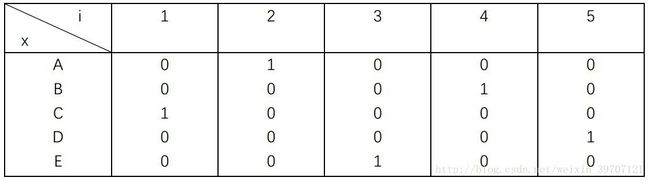
       TSP问题就是在一城市集合{A,B,C,…}中找出一个最短且经过每个城市各一次并回到起点的路径。为了将TSP问题映射到一神经网络的动态演化过程，首先必须找到一合适的表示方法。任一城市在最终路径上的次序可用一N维矢量表示。以10城市为例，如果城市A是第6个访问，则可以用0000010000，即只有第6个神经元的输出为1，其余都是0。为了表示表示所有城市，就需要N×N阶矩阵。例如5个城市，访问顺序顺序是CAEBD，那么可以用这样的方阵表示。

访问距离是：

      对于走过的每一条可能的路径，每个城市都只能走过一次且需要一一走过每个城市，因此这一方阵中的每一行和每一列都只能有一个元素为1，其余元素为0。这边是TSP问题的约束条件。具有上述约束条件的每一路径可用一换位阵表示。

      将TSP问题映射为神经网络动力系统可用以下步骤完成：

1)     将TSP问题的每一条可能路径用一换位矩阵表示，并给出相应的距离表示试；

2)     将TSP问题的换位阵集合与由N个神经元构成的神经元阵列相对应；每一条路径所对应的换位阵的各元素与相应的神经元稳态输出对应；

3)     找出一反应TSP约束优化问题的能连函数E；

4)     求出使E取极小值的神经网络连接权重矩阵和偏置参数。

      由上述步骤设计的神经网络可用于相应TSP问题的求解，网络的稳态输出即就是TSP问题的局域优化解，同时也是能量函数的极小点。网络的搜索时间即就是网络到达稳态的时间，计算过程也就是网络的动力学过程。

       将每一条有效路径用一换位矩阵表示，神经元的输出用 表示，下表x表示城市，i表示访问次序。为了求解TSP问题，必须找到这样的神经网络，是它的计算能量的极小点对应最佳路径。具体来说，由计算能量找到的极小点状态必须构成换位矩阵，并使其路径最短，由Hopfield和Tank给出的能量函数可以表示为：

      A，B，C>0，当且仅当路径矩阵的每一行不多于一个1时，式中第一项为0；当且仅当路径矩阵的每一列不多于一个1时，式中第二项为0；当且仅当路径矩阵中为1的元素是N时，式中第三项为0，因此这三项保证了所有路径的有效性。除此之外为保证路径最短必须加入有关路径长度的信息，可用下式表示：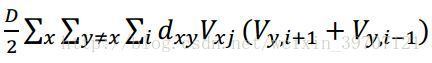

      由此可以得到N个城市TSP问题的能量函数：

相应的神经网络可以描述为：

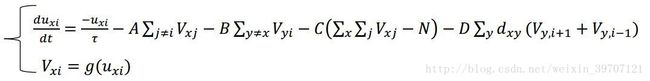
      当神经元取0、1（或1、-1），且g(x)取sgn函数时，上式化为二值模型，当g(x)取单调连续的sigmoid函数时，上式即就是连续的Hopfield网络模型。

       理论分析和实验结果标明在通用计算机上计算TSP问题时，用二值模型比采用连续模型快得多；而在连续模型中，由于神经元非线性函数斜率的可变性，神经网络多一个可调参数，它与玻尔兹曼机中的温度参数相对应，若与模拟退火或其它方法相结合，即可获得全局最优解或质量更好的解。

       若A，B，C，D充分大，则网络的所有稳态输出矢量都代表一有效路径，此时的E值就是路径的长度，且与E的极小点相对应。相应地，网络的连接权值矩阵T和外加激励可描述如下：

其中：

       能量函数中前三项适用于一般的TSP问题，而其它四项与某一具体特定的TSP问题有关。

       用神经网络方法求解各种组合优化问题的关键是把问题映射为一神经网络动力系统，并写出相应的能量函数表达式和动力学方程，它们应满足问题的约束条件；最后研究神经网络的动力学过程，以保证网络的稳态输出与能量函数的极小值和组合优化问题的解相对应。在TSP问题中，解的质量与网络的初值、参数A，B，C，D、城市分布特性、神经元非线性特性函数等的选取密切相关，不同的选取将导致完全不同的结果。

       通过神经元连接权值矩阵T及网络本身动力学研究，有助于确定或选择参数A，B，C，D。其中方法之一是确定连接权值矩阵的特征值和相应的特征矢量、子空间方法，由特征矢量和特征空间/子空间确定神经网络向最优稳态解的运动，以选择有效子空间和保证有效解的参数A，B，C，D。

       事实上，目前神经优化都是基于以下两点进行的：（1）神经网络是稳定的，即它必然演化到网络的渐进平衡点；（2）神经网络的渐进稳定平衡点恰是能量函数E的极小值点。

总结一下

       Hopfield神经网络特点：（1）反馈性神经网络可以用离散变量也可以用连续变量，考虑输出与输入在时间上的延迟，需要用动态方程（差分方程或微分方程）来描述神经元和系统的数学模型。（2）前馈神经网络采用误差修正法，计算一般比较慢，收敛速度也慢。反馈型神经网络Hopfield神经网络主要采用Hebb规则，一般情况下收敛速度很快，它与电子电路存在对应关系，使得该网络易于理解和易于硬件实现。（3）Hopfield神经网络也具有类似于前馈神经网络的应用，而在优化计算方面的应用更加显示出Hopfield神经网络的特点。由于联想记忆和优化计算是对偶的，当用于联想记忆时，通过样本模式的输入来给定网络的稳定状态，经过学习求得突触权重值；当用于优化计算时，以目标函数和约束条件建立系统的能量函数，确定突触权重值，网络演化到稳定状态，既是优化问题的解。

        后面还会有Hopfield神经网络处理联想记忆、TSP问题、snake模型与Hopfield神经网络结合这3片博文，欢迎关注。

Reference：

1.《人工神经网络及其融合应用技术》

2.《神经网络计算》焦李成

3.季策. 时滞递归神经网络的动态特性研究[D]. 东北大学, 2005.

4.《神经网络设计》Martin T.Hagan

5.

Potvin J Y, Smith K A. Artificial neuralnetworks for combinatorial optimization[M]//Handbook of metaheuristics.Springer US, 2003: 429-455.

6.http://web.cs.ucla.edu/~rosen/161/notes/hopfield.html

7.http://www.asimovinstitute.org/neural-network-zoo/

8.http://mlexplore.org/2017/03/12/hopfield-networks-in-go/