PCA、LDA降维——应用于wine葡萄酒数据集

参考教程：https://mp.weixin.qq.com/s/QqqLAxx92v_HOg7QBKrK6A

一、wine数据集介绍

sklearn的wine数据，它有178个样本，13个特征（Alcohol ，Malic acid ，Ash等），总共分为三类。

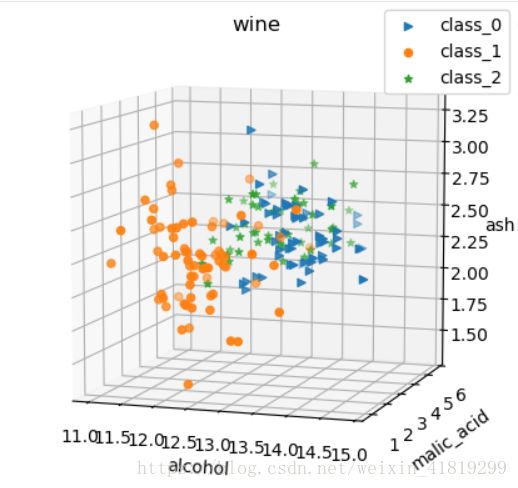
二、查看三个特征下的数据分布

#葡萄酒数据集+PCA
import matplotlib.pyplot as plt#画图工具
from mpl_toolkits.mplot3d import Axes3D
from sklearn import datasets
data=datasets.load_wine()
X=data['data']
y=data['target']
###########

#选取三个特征查看IRIS数据分布
ax = Axes3D(plt.figure())
for c,i,target_name in zip('>o*',[0,1,2],data.target_names):
    ax.scatter(X[y==i ,0], X[y==i, 1], X[y==i,2], marker=c, label=target_name)
ax.set_xlabel(data.feature_names[0])
ax.set_ylabel(data.feature_names[1])
ax.set_zlabel(data.feature_names[2])
ax.set_title("wine")
plt.legend()
plt.show()

注意：与鸢尾花数据集相比，绘图时的区别是‘>o*’和marker

三、不标准化下的降维前和降维后

#选取两个特征查看IRIS数据分布
# ax = plt.figure()
# for c, i, target_name in zip("rgb", [0, 1, 2], data.target_names):
#     plt.scatter(X[y == i, 0], X[y == i, 1], c=c, label=target_name)
# plt.xlabel(data.feature_names[0])
# plt.ylabel(data.feature_names[1])
# plt.title("wine")
# plt.legend()
# plt.show()
#利用PCA降维，降到二维
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X_p =pca.fit(X).transform(X)
ax = plt.figure()
for c, i, target_name in zip("rgb", [0, 1, 2], data.target_names):
    plt.scatter(X_p[y == i, 0], X_p[y == i, 1], c=c, label=target_name)
plt.xlabel('Dimension1')
plt.ylabel('Dimension2')
plt.title("wine")
plt.legend()
plt.show()

 

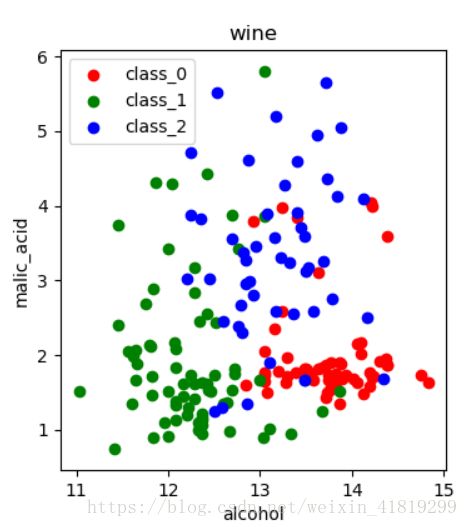
降维前：

 

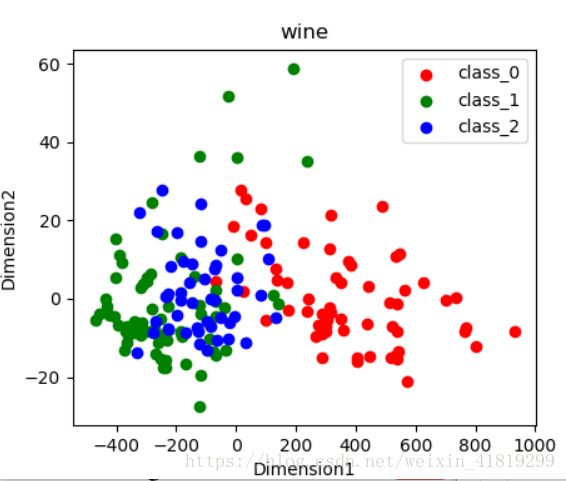
降维后

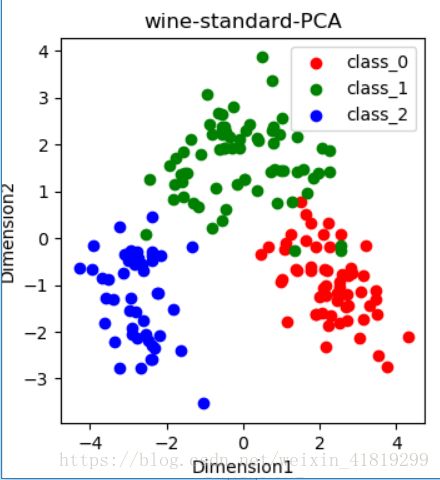
四、标准化后做PCA降维

#标准化后做PCA
from sklearn.preprocessing import StandardScaler
X=StandardScaler().fit(X).transform(X)
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X_p =pca.fit(X).transform(X)
ax = plt.figure()
for c, i, target_name in zip("rgb", [0, 1, 2], data.target_names):
    plt.scatter(X_p[y == i, 0], X_p[y == i, 1], c=c, label=target_name)
plt.xlabel('Dimension1')
plt.ylabel('Dimension2')
plt.title("wine-standard-PCA")
plt.legend()
plt.show()

标准化后均值为0，标准差为1

五、不需要标准化的LDA有监督降维

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
lda = LDA(n_components=2)
X_r =lda.fit(X,y).transform(X)
ax = plt.figure()
for c, i, target_name in zip("rgb", [0, 1, 2], data.target_names):
    plt.scatter(X_r[y == i, 0], X_r[y == i, 1], c=c, label=target_name)
plt.xlabel('Dimension1')
plt.ylabel('Dimension2')
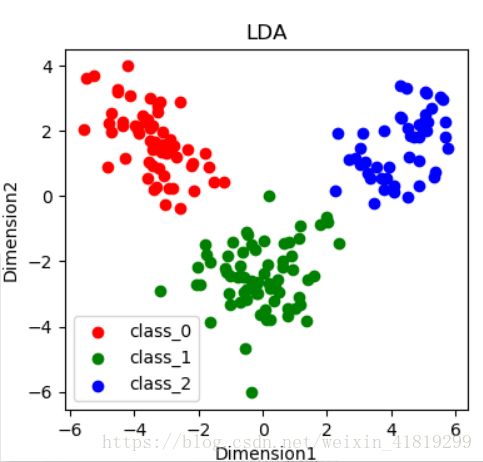
plt.title("LDA")
plt.legend()
plt.show()

 

有监督在程序中表现在X_r =lda.fit(X,y).transform(X)，用到了标签y。

 

与PCA相比，LDA能够将三类样本完全分开，且同类样本之间更为密集，一般而言，有监督的LDA更加准确。

六、PCA、LDA原理

PCA：

  通过坐标轴转换，寻找数据分布的最优子空间。用协方差矩阵前N个最大特征值对应的特征向量构成映射矩阵，然后原始矩阵左乘映射矩阵实现降维。特征向量可以理解为坐标转换中新坐标轴的方向，特征值表示对应特征向量上的方差。

LDA：

   将带标签的数据通过投影降低维度，使投影不同类距离远，同类点分散程度小。