吴恩达机器学习笔记(二)(多变量特征缩放,特征选择,正规方程)
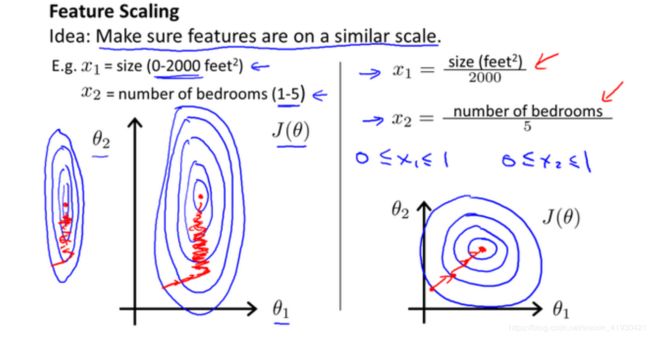
当出现变量之间范围相差较大时,可以将其特征缩放标准化后,使梯度下降法的速度提高。
下面的作业题中,X数据的第一列代表房间的面积,第二列代表房间数。相差过大所以需要特征缩放
补充知识:标准差=根号方差。
默认是std(x,0,1),第二个位置0代表方差的分母是n,1代表方差分母是n-1,第三个位置,0代表按照行来计算标准差,1代表按列来计算标准差。
特征缩放函数 (x=(x-u平均值)/标准差)
function [X_norm, mu, sigma] = featureNormalize(X)
X_norm = X;
mu = zeros(1, size(X, 2));
sigma = zeros(1, size(X, 2));
mu = mean(X); % m.u中记录X的平均值
sigma = std(X); % X的标准差
X_norm = (X-repmat(mu,size(X,1),1))./repmat(sigma,size(X,1),1);
end
梯度下降函数,返回θ,J
function [theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters)
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
theta = theta - alpha / m * X' * (X * theta - y);
J_history(iter) = computeCostMulti(X, y, theta);
end
end
代价函数,返回J到梯度函数里
function J = computeCostMulti(X, y, theta)
m = length(y); % number of training examples
J = 0;
J = sum((X * theta - y).^2) / (2*m);
end
主函数
clear ; close all; clc;
data = load('ex1data2.txt'); %自己想研究的数据,
X = data(:, 1:2); %这次每一个特征里有三个数据可以训练
y = data(:, 3);
m = length(y);
[X mu sigma] = featureNormalize(X);
X = [ones(m, 1) X];
alpha = 0.01;
num_iters = 400;
theta = zeros(3, 1);
[theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters);
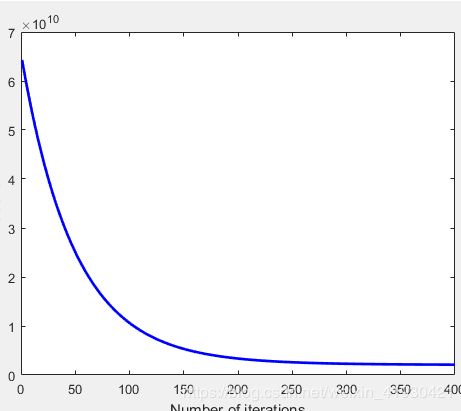
figure;
plot(1:numel(J_history), J_history, '-b', 'LineWidth', 2);
xlabel('Number of iterations');
ylabel('Cost J');
%% 预测X是2650 3时y的值,注意前面有个1斜体样式
price = [1 (([2650 3]-mu) ./ sigma)] * theta ;
J的变化
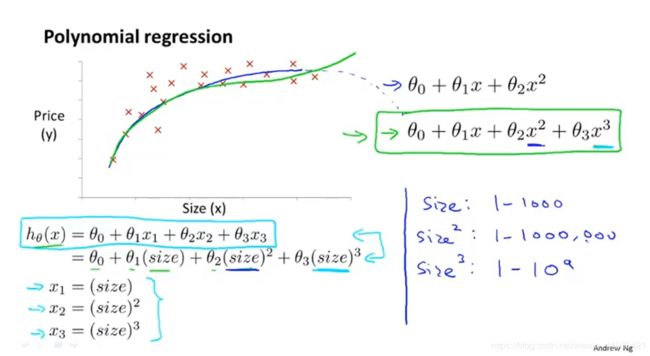
下图可以看到,选择1,X,X2,X3来表示一组特征,但是每一次特征里的应当所代表的取值范围都成平方立方次扩大状态。
如果它的趋势下降可以用根号几来做特征
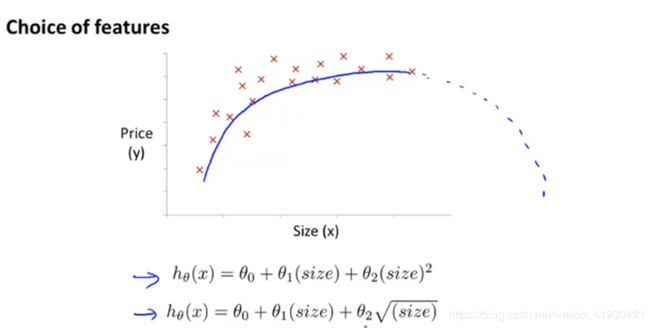
这里给出以三角多项式为特征和以上面的X的几次方为特征进行非线性拟合的matlab程序
图解机器学习上的随机梯度线性拟合
clear
n=50;N=1000;x=linspace(-3,3,n)';
X=linspace(-3,3,N)';
pix=pi*x;
y=sin(pix)./(pix)+0.1*x+0.05*randn(n,1); %一个非线性函数,下面将使用三角多项式拟合
p(:,1)=ones(n,1);
P(:,1)=ones(N,1);
for j=1:15
p(:,2*j)=sin(j/2*x);
p(:,2*j+1)=cos(j/2*x);
P(:,2*j)=sin(j/2*X);
P(:,2*j+1)=cos(j/2*X);
end
t=p\y;F=P*t;
figure(1);
clf; hold on;
axis([-2.8 2.8 -0.5 1.2]);
plot(X,F,'g-');
plot(x,y,'bo');
clear;
n=50;N=1000;x=linspace(-3,3,n)';
X=linspace(-3,3,N)';
pix=pi*x;
y=sin(pix)./(pix)+0.1*x+0.05*randn(n,1);
p(:,1)=ones(n,1);
P(:,1)=ones(N,1);
for j=1:15 %超出将过拟合
p(:,2*j)=x.^j;
p(:,2*j+1)=x.^(j+1);
P(:,2*j)=X.^j;
P(:,2*j+1)=X.^(j+1);
end
%% 生成拟合函数
t=p\y;
F=P*t;
figure(1);
clf; hold on;
axis([-2.8 2.8 -0.5 1.2]);
plot(X,F,'g-');
plot(x,y,'bo');
在上面的拟合过程中可以发现,在使用X几次方为特征拟合的时候会出现矩阵的秩过小的情况,就是因为x的范围不匹配了。
《图解机器学习》中的高斯核函数的梯度下降算法进行非线性拟合方式
我们可以写个小k记录迭代次数,发现这狗东西都是要进行上万次迭代的。 
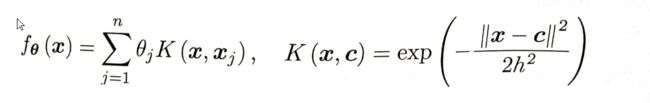
c是x数据集中的随机一个
clear;
n=50;N=1000;x=linspace(-3,3,n)'; %50个训练样本点,1000是为了更好地体现拟合非线性函数的连续性与准确性
X=linspace(-3,3,N)';
pix=pi*x;
y=sin(pix)./(pix)+0.1*x+0.05*randn(n,1);
%%
hh=2*0.23^2; %高斯核函数的带宽0.23
t0=randn(n,1); %50个方差为一的随机数组成一个列向量
e=0.1; %梯度下降的学习率
for o=1:n*1000 %循环一个非常大的数
i=ceil(rand*n); %生成一个0-50的随机数
ki=exp(-(x-x(i)).^2/hh); %核函数里的k,50长度的列向量的所有值减去其中一个值再带入
t=t0-e*ki*(ki'*t0-y(i)); %每一次的更新值θ
if norm(t-t0)<0.000001 , %与上一次的更新值θ相差如果小于最小误差则迭代结束
break,
end
t0=t;
end
%%生成拟合函数
K=exp(-(repmat(X.^2,1,n)+repmat(x.^2',N,1)-2*X*x')/hh);
F=K*t; %θ乘K就是f核函数
figure(1);
clf; hold on;
axis([-2.8 2.8 -0.5 1.2]);
plot(X,F,'g-');
plot(x,y,'bo');
正规方程
正规方程的方法使求得最优的代价函数解的步骤变得只有一步

对于下面这样的凸函数只需要知道对θ求导等于零,即可知道最小代价函数值所对应的θ。
而对于多参数变量只需要求偏导即可
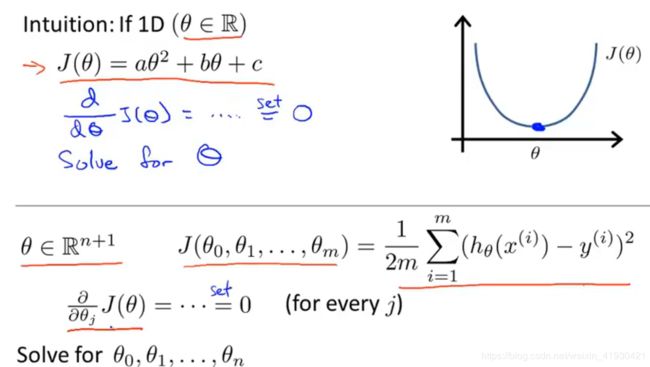
现在我们得到m组特征,其中特征x和特征y都有m个,(当然x的种类有x0,x1,x2…xn一共(n+1)种)
现在我们把x单独拎出来,做一个种类上的列向量,代表了x一共有n+1种(n+1)行。
然后将其扩展后就是(n+1)行*m列。
再将它转置
下面例子是代表最简单的情况,x只有两个种类x0(等于1)和x1

数学上可以证明它,会得到最小值,我佛了
pinv代表求逆
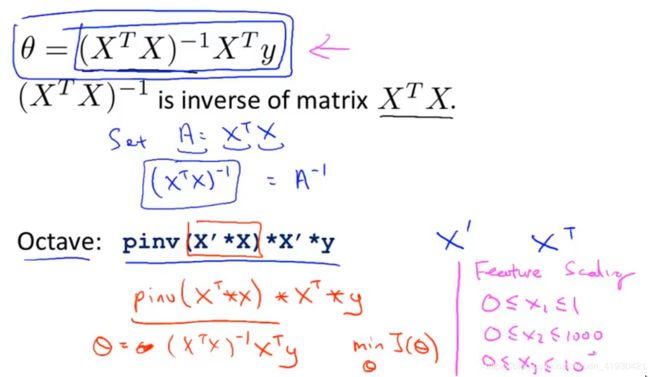
使用正规方程时,计算的速度更快。
主函数
clear ; close all; clc;
data = load('ex1data2.txt'); %自己想研究的数据,
X = data(:, 1:2); %这次每一个特征里有三个数据可以训练
y = data(:, 3);
m = length(y);
X = [ones(m, 1) X];
theta = normalEqn(X, y);
%%预测,可以和上面的梯度下降进行比较
price = [1 (([2650 3]-mu) ./ sigma)] * theta ;
正规方程函数
function [theta] = normalEqn(X, y)
theta = zeros(size(X, 2), 1);
theta = pinv( X' * X ) * X' * y;
end
当你在使用正规方程求最小的代价函数时,特征缩放就显得不重要了。尽管各种x的取值范围是差异巨大的,还是可以很快的到达最低的代价函数值。

如果选择梯度下降法,那你需要选择学习率,要迭代,正规方程都不需要。但是正规方程需要计算一个逆矩阵,这个计算的速度取决于矩阵维度。所以当特征种类变多的时候,有限选择梯度下降法。
当使用正规方程时会遇到XTX是不可逆矩阵的时候,奇异或病态时,那么pinv仍然可以解出其逆矩阵,这东西有操作的呀…。

就比如下面提到的
第一种是两个特征之间是线性关系的。那么矩阵的秩就会接近零,变成一个病态矩阵,如果有太多种类的特征(X_1…X_n)了,而你的训练样本远远小于n。那么在这个矩阵也会变得非常病态。