opencv(19) 离散傅里叶变换
离散傅里叶变换(Discrete Founer Transform,缩写为DFT),是指傅里叶变换在时域和频域上都呈现离散的形式,将时域信号的采样变换为在离散时间傅里叶变换(DTFT)频域的采样。在形式上,变换两端(时域和频域上)的序列是有限长的,而实际上这两组序列都应当被认为是离散周期信号的主值序列。即使对有限长的离散信号做DFT,也应当对其经过周期延拓成为周期信号再进行变换。在实际应用中,通常采用快速傅里叶变换来高效计算DFT。
1. 离散傅里叶变换的原理
简单来说,对一张图像使用傅里叶变换就是将它分解成正弦和余弦两部分,也就是将图像从空间域(spatia ldomain)转换到频域(frequency domain)。
这一转换的理论基础为:任一函数都可以表示成无数个正弦和余弦函数的和的形式。傅里叶变换就是一个用来将函数分解的工具。
二维图像的傅里叶变换可以用以下数学公式表达。
F ( k , l ) = ∑ i = 0 N − 1 ∑ j = 0 N − 1 f ( i , j ) s − i 2 π ( k i N + l j N ) F(k,l)=\sum_{i=0}^{N-1}\sum_{j=0}^{N-1}f(i,j)s^{-i2\pi(\frac{ki}{N}+\frac{lj}{N})} F(k,l)=∑i=0N−1∑j=0N−1f(i,j)s−i2π(Nki+Nlj)
e i x = c o s x + i s i n x e^{ix}=cosx+isinx eix=cosx+isinx
式中f是空间域(spatialdomain)值,F是频域(frequencydomain)值。转换之后的频域值是复数,因此,显示傅里叶变换之后的结果需要使用实数图像(real image)加虚数图像(complex image)或者幅度图像(magitude image)加相位图像(phaseimage)的形式。在实际的图像处理过程中,仅仅使用了幅度图像,因为幅度图像包含了原图像的几乎所有我们需要的几何信息。然而,如果想通过修改幅度图像或者相位图像的方法来间接修改原空间图像,需要使用逆傅里叶变换得到修改后的空间图像,这样就必须同时保留幅度图像和相位图像了。
在此示例中,我们将展示如何计算以及显示傅里叶变换后的幅度图像。由于数字图像的离散性,像素值的取值范围也是有限的。比如在一张灰度图像中,像素灰度值一般在0到255之间。因此,我们这里讨论的也仅仅是离散傅里叶变换(DFT)。如果需要得到图像中的几何结构信息,那你就要用到它了。
在频域里面,对于一輻图像,高频部分代表了图像的细节、纹理信息;低频部分代表了图像的轮廓信息。如果对一幅精细的图像使用低通滤波器,那么滤波后的结果就只剩下轮廓了。这与信号处理的基本思想是相通的。如果图像受到的噪声恰好位于某个特定的“频率”范围内,则可以通过滤波器来恢复原来的图像。傅里叶变换在图像处理中可以做到图像增强与图像去噪、图像分割之边缘检测、图像特征提取、图像压缩等。
2. dft()函数详解
dft函数的作用是对一维或二维浮点数数组进行正向或反向离散傅里叶变换。
C++:
void dft(InputArray src,OutputArray dst,int fIags=0,intnonzeroRows=0)
- 第一个参数,InputArray类型的src。输入矩阵,可以为实数或者虚数。
- 第二个参数,OutputArray类型的dst。函数调用后的运算结果存在这里,其尺寸和类型取决于标识符,也就是第三个参数flags。
- 第三个参数,int类型的flags。转换的标识符,有默认值0,取值可以为表6.1中标识符的结合。
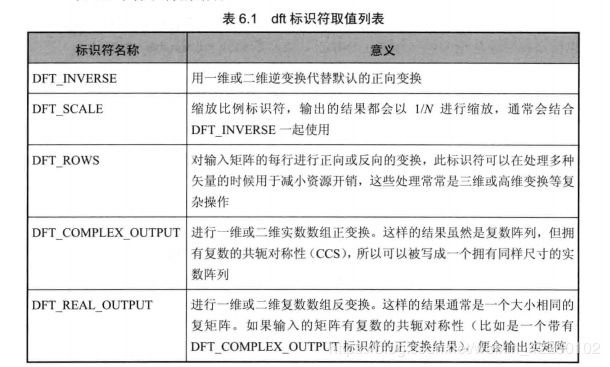
- 第四个参数,int类型的nonzeroRows,有默认值0。当此参数设为非零时(最好是取值为想要处理的那一行的值,比如C.rows),函数会假设只有输
入矩阵的第一个非零行包含非零元素(没有设置DFT_INVERSE标识符),或只有输出矩阵的第一个非零行包含非零元素(设置了DFTINVERSE标
识符)。这样的话,函数就可对其他行进行更高效的处理,以节省时间开销。这项技术尤其是在采用DFT计算矩阵卷积时非常有效。
讲解完函数的参数含义,下面我们看一个用dft函数计算两个二维实矩阵卷积的示例核心片段。
void convolveDFT(InputArray A, InputArray B, OutputArray C){
//[1]初始化输出矩阵
C.create(abs(A.rows - B.rows) + 1, abs(A.cols - B.cols) + 1, A.type());
Size dftSize;
//[2]计算DFT变幻的尺寸
dftSize.width = getOptimalDFTSize(A.cols + B.cols - 1);
dftSize.height = getOptimalDFTSize(A.rows + B.rows - 1);
//[3]分配临时缓冲区并初始化置零
Mat tempA(dftSize, A.type(), Scalar::all(0));
Mat tempB(dftSize, B.type(), Scalar::all(0));
//[4]分别复制A和B到tempA和tempB的左上角
Mat roiA(dftSize, A.type(), Scalar::all(0));
A.copyTo(roiA);
Mat roiB(dftSize, B.type(), Scalar::all(0));
B.copyTo(roiB);
//[5]快速傅里叶
dft(tempA, tempA, 0, A.rows);
dft(tempB, tempB, 0, B.rows);
//[6]频谱相乘
mulSpectrums(tempA, tempB, tempA);
//[7]将结果转换为频域
dft(tempA, tempA, DFT_INVERSE + DFT_SCALE, C.rows);
//将结果复制到C中
tempA(Rect(0, 0, C.cols, C.rows)).copyTo(C);
}
3. 返回DFT最优尺寸大小:getOptimaIDFTSize()函数
getOptimalDFTSize函数返回给定向量尺寸的傅里叶最优尺寸大小。为了提高离散傅里叶变换的运行速度,需要扩充图像,而具体扩充多少,就由这个函数来计算得到。
C++:
int getOptimalDFTSize(int vecsize)
此函数的唯一一个参数为int型的vecsize,向量尺寸,即图片的rows.cols。
4. 扩充图像边界:copyMakeBorder()函数
copyMakeBorder函数的作用是扩充图像边界。
C++:
void copyMakeBorder(InputArray src,OutputArray dst,int top,int bottom,int left,int right,int borderType,const Scalar& value=Scalar());
- 第一个参数,InputArray类型的src,输入图像,即源图像,填Mat类的对象即可。
- 第二个参数,OutputArray类型的dst,函数调用后的运算结果存在这里,即这个参数用于存放函数调用后的输出结果,需和源图片有一样的尺寸和类型,且size应该为Size(src.cols+left+right,src.rows+top+bottom)。
- 接下来的4个参数分别为int类型的top、bottom、left、nght,分别表示在源图像的四个方向上扩充多少像素,例如top=2,bottom=2,left=2,right=2就意味着在源图像的上下左右各扩充两个像素宽度的边界。
- 第七个参数,borderType类型的,边界类型,常见取值为BORDER_CONSTANT,可参考borderlnterpolate()得到更多的细节。
- 第八个参数,const Scalar类型的value,有默认值Scalar(),可以理解为默认值为0。当borderType取值为BORDER_CONSTANT时,这个参数表示
边界值。
5. 计算二维矢量的幅值:magnitude()函数
magnitude()函数用于计算二维矢量的幅值。
C++:
void magnitude(InputArray x,InputArray y,OutputArray magnitude)
- 第一个参数,InputArray类型的,表示矢量的浮点型X坐标值,也就是实部。
- 第二个参数,InputArray类型的y,表示矢量的浮点型Y坐标值,也就是虚部。
- 第三次参数,OutputArray类型的magnitude,输出的幅值,它和第一个参数x有着同样的尺寸和类型。
下式可以表示magnitude()函数的原理:
d s t ( I ) = x ( I ) 2 + y ( I ) 2 dst(I)=\sqrt{x(I)^{2}+y(I)^{2}} dst(I)=x(I)2+y(I)2
6. 计算自然对数:log()函数
log()函数的功能是计算每个数组元素绝对值的自然对数。
C++:
void log(InputArray src,OutputArray dst)
第一个参数为输入图像,第二个参数为得到的对数值。其原理如下。
d s t ( I ) = { l o g ∣ s r c ( I ) ∣ i f s r c ( I ) ≠ 0 C o t e r w i s e dst(I)=\left\{\begin{matrix} log|src(I)| &if src(I)\neq0 \\ C &oterwise \end{matrix}\right. dst(I)={log∣src(I)∣Cifsrc(I)=0oterwise
7. 矩阵归一化:normalize()函数
C++:
void normalize(InputArray src,OutputArray dst,double alpha=1,double beta=0,int norm_type=NORM_L2,int dtype=-1,InputArray mask=noArray())
- 第一个参数,InputArray类型的src。输入图像,即源图像,填Mat类的对象即可。
- 第二个参数,OutputArray类型的dst。函数调用后的运算结果存在这里,和源图片有一样的尺寸和类型。
- 第三个参数,double类型的alpha。归一化后的最大值,有默认值1。
- 第四个参数,double类型的beta。归一化后的最大值,有默认值0;
- 第五个参数,int类型的norm_type。归一化类型,有NORM_INF、NORM_LI、NORM_L2和NORM_MINMAX等参数可选,有默认值NORM_L2。
- 第六个参数,int类型的dtype,有默认值-1。当此参数取负值时,输出矩阵和src有同样的类型,否则,它和src有同样的通道数,且此时图像深度为
CV_MAT_DEPTH(dtype)。 - 第七个参数,InputArray类型的mask,可选的操作掩膜,有默认值noArray()。