吴恩达机器学习第二次作业-Logstic Regression

（一）将数据可视化

addpath('文件路径')
data = load('ex2data1.txt')
X = data(:,[1,2])
y = data(:,3)
plotData(X,y)

%plotData函数
function plotData(X,y)
figure;hold on;
pos = find(y == 1);
neg = find(y == 0);
plot(X(pos, 1), X(pos, 2), 'k+','LineWidth', 2, ...
'MarkerSize', 7);
plot(X(neg, 1), X(neg, 2), 'ko', 'MarkerFaceColor', 'y', ...
'MarkerSize', 7);

（二）代价函数和梯度

[m,n] = size(X)
X = [ones(m,1),X]
initial_theta = zeros(n+1,1)
[cost,grad] = costFunction(theta,X,y)

%代价函数costFunction
function [J,grad] = costFunction(theta,X,y)
m = length(y)
J = 0;
grad = zeros(size(theta));
J= -1 * sum( y .* log( sigmoid(X*theta) ) + (1 - y ) .* log( (1 - sigmoid(X*theta)) ) ) / m ; 
grad = ( X' * (sigmoid(X*theta) - y ) )/ m ;
end;

（三）优化

options = optimset('GradObj', 'on', 'MaxIter', 400);
%<‘GradObj’, ‘on’>代表在fminunc函数中使用自定义的梯度下降函数 ， < ‘MaxIter’, 400>代表最大迭代次数为400。
[theta,cost] = ...fminunc(@(t)(costFunction(t, X, Y)), initial_theta, options);
至此我们得到了theta
接下来我们就可以通过判断sigmoid(X*theta)是否>=0.5来判断类别

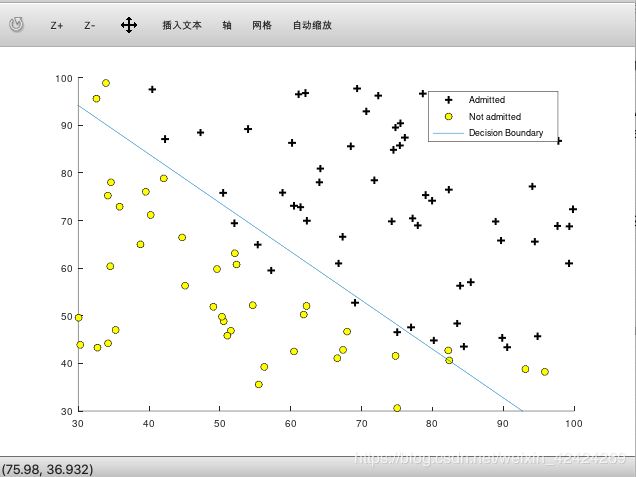
（四）画出决策边界

function plotDecisionBoundary(theta, X, y)
plotData(X(:,2:3), y);
hold on
if size(X, 2) <= 3
    % Only need 2 points to define a line, so choose two endpoints
    plot_x = [min(X(:,2))-2,  max(X(:,2))+2];
    plot_y = (-1./theta(3)).*(theta(2).*plot_x + theta(1));
    plot(plot_x, plot_y)
    legend('Admitted', 'Not admitted', 'Decision Boundary')
    axis([30, 100, 30, 100])
    
else
    u = linspace(-1, 1.5, 50);
    v = linspace(-1, 1.5, 50);
    z = zeros(length(u), length(v));
    for i = 1:length(u)
        for j = 1:length(v)
            z(i,j) = mapFeature(u(i), v(j))*theta;
        end
    end
    z = z'; 
    contour(u, v, z, [0, 0], 'LineWidth', 2)
end
hold off

end

得到图

如果得到的决策边界不是这样的话，我认为多半是代价函数（costFunction）错了