判别分析原理及R语言实现
判别分析内容
判别分析做的好能挖掘数据最大的价值。判别分析(discriminat analysis)他要解决的问题是在一些已知研究对象已经用某种方法分成若干类的情况下,确定新的样品属于已知类别中的哪一类。如已知健康人和冠心病人的血压、血脂等资料,以此建立判别函数,对新样品分类进行预测。在模式识别领域(比如人脸识别,舰艇识别等图形图像识别领域)中有非常广泛的应用。判别分析在处理问题时,通常要给出一个衡量新样品与各已知类别接近程度的描述统计模型,即判别函数,同时也需要指定一种判别规则,以判断新样品的归属。判别规则可以是确定性的也可以是统计性的分别对应Fisher判别和Bayes判别。今天明明同学给大家讲讲《判别分析原理及R语言实现》。
目录:
1.线性判别分析
2.距离判别分析
3.二次判别分析
4.Bayes判别分析
1、线性判别分析
提出:
最早由fisher(1936)提出,用于花卉分类上,将花卉的各种特征(如花瓣长与宽,花萼长与宽等)利用线性组合方法变成单变量值,再以单值比较方法来判别事物间的差别。
示例:
以两类判别为例说明。设有两类样品,分别为n1,n2个样品,各测得p个指标,观察值如下表所示。
| 序号 | 变量 | 分类 | |||
| X1 | X2 | … | Xp | Y | |
| 1 | x11 | x12 | … | x1p | 1 |
| 2 | x21 | x22 | … | x2p | 1 |
| … | … | … | … | … | 1 |
| n1 | xn11 | xn12 | … | xn1p | 1 |
| 1 | … | … | … | … | 2 |
| 2 | … | … | … | … | 2 |
| … | … | … | … | … | 2 |
| n2 | xn21 | xn22 | … | xn2p | 2 |
可以预设线性判别函数为Y = a1X1+ a2X2+……+ apXp = a’X。使得该判别函数能根据指标X1,X2,XP之值区分各样品归属哪一类。
步骤:
1、 求Fisher线性判别函数(Fisher线性判别准则要求各类之间的变异尽可能地大,而各类内部的变异尽可能地小,变异用离均差平方和表示)
2、 计算判别界值(求的ai后,代入判别函数式即得判别函数)
3、 建立判别标准
下面对R语言实现过程详细介绍。
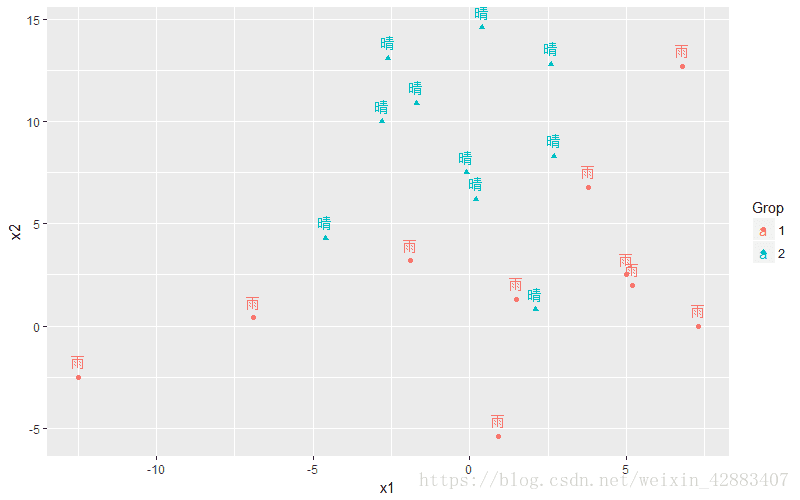
根据经验,今天和昨天气温差x1和x2是预报明天下雨或不下雨的两个重要因子,实验记录如下表格,试问,今天测得x1=8.1,x2=2.0,明天应该预报下雨还是晴天?
| Grop | x1 | x2 | weather |
|---|---|---|---|
| 1 | -1.9 | 3.2 | 雨 |
| 1 | -6.9 | 0.4 | 雨 |
| 1 | 5.2 | 2 | 雨 |
| 1 | 5 | 2.5 | 雨 |
| 1 | 7.3 | 0 | 雨 |
| 1 | 6.8 | 12.7 | 雨 |
| 1 | 0.9 | -5.4 | 雨 |
| 1 | -12.5 | -2.5 | 雨 |
| 1 | 1.5 | 1.3 | 雨 |
| 1 | 3.8 | 6.8 | 雨 |
| 2 | 0.2 | 6.2 | 晴 |
| 2 | -0.1 | 7.5 | 晴 |
| 2 | 0.4 | 14.6 | 晴 |
| 2 | 2.7 | 8.3 | 晴 |
| 2 | 2.1 | 0.8 | 晴 |
| 2 | -4.6 | 4.3 | 晴 |
| 2 | -1.7 | 10.9 | 晴 |
| 2 | -2.6 | 13.1 | 晴 |
| 2 | 2.6 | 12.8 | 晴 |
| 2 | -2.8 | 10 | 晴 |
R语言中进行线性判别得函数为lda()
形式如下:
lda(formula , data,……)
formula和上次明明同学介绍的回归分析中的形式一样。
Data为数据框。
1、首先把数据加载到R语言中 ,然后画出数据散点图,初步观察数据分布。
#导入数据
weatherData <- read.table("clipboard" , header = T);
#将Grop中的1,2转换成因子变量
weatherData$Grop <- as.factor(weatherData$Grop)
#画出散点图,初步观察数据分布情况
ggplot(data = weatherData , aes(x = x1 , y = x2 , shape = Grop ,color = Grop)) +
geom_point() + geom_text(aes(label = weather) , vjust = -0.8);> #加载分析所需要的包
> require(MASS);
> #建立判别函数
> weatherLd <- lda(Grop ~ x1 + x2 , data = weatherData);
> #查看函数结果
> weatherLd;
Call:
lda(Grop ~ x1 + x2, data = weatherData)
Prior probabilities of groups:
1 2
0.5 0.5
Group means:
x1 x2
1 0.92 2.10
2 -0.38 8.85
Coefficients of linear discriminants:
LD1
x1 -0.1035305
x2 0.22479573、用训练的判别函数对源数据进行检测
> #根据线性函数模型预测所属类别
> weatherPredict <- predict(weatherLd)
> #预测的所属类的结果
> newGrop <- weatherPredict$class
> #显示预测前后分组结果
> cbind(weatherData$Grop , weatherPredict$x , newGrop)
LD1 newGrop
1 1 -0.28674901 1
2 1 -0.39852439 1
3 1 -1.29157053 1
4 1 -1.15846657 1
5 1 -1.95857603 1
6 1 0.94809469 2
7 1 -2.50987753 1
8 1 -0.47066104 1
9 1 -1.06586461 1
10 1 -0.06760842 1
11 2 0.17022402 2
12 2 0.49351760 2
13 2 2.03780185 2
14 2 0.38346871 2
15 2 -1.24038077 1
16 2 0.24005867 2
17 2 1.42347182 2
18 2 2.01119984 2
19 2 1.40540244 2
20 2 1.33503926 2由结果可知,两类中分别有一个判别错误,判对的共有18对。判对率为18/20=90%
4、构造混淆矩阵,求出判对率
> tab <- table(weatherData$Grop , newGrop)
> tab
newGrop
1 2
1 9 1
2 1 9
> sum(diag(prop.table(tab)))
[1] 0.9由这个结果也可以看出,判对率为90%。求出的判别函数为y=-0.1035x1+0.2248x2 。
画出分类线为:
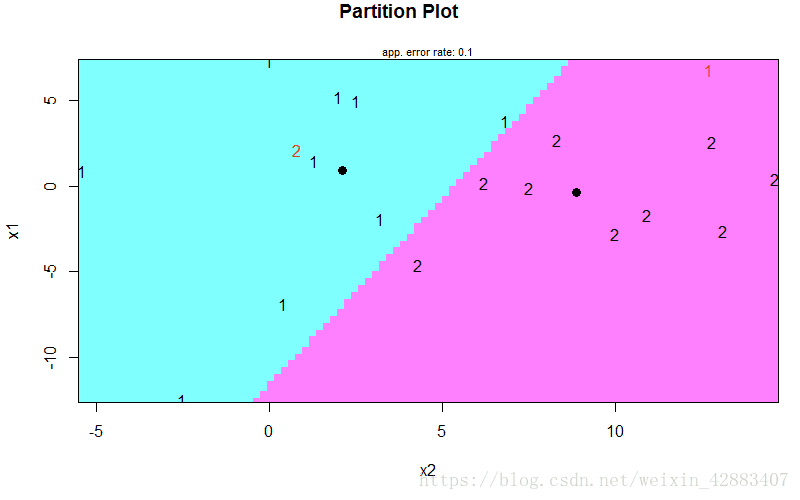
5、对新数据进行预测
> predict(weatherLd , newdata = data.frame(x1 = 8.1 , x2 = 2))
$class
[1] 1
Levels: 1 2
$posterior
1 2
1 0.9327428 0.06725717
$x
LD1
1 -1.591809由结果可以看出,当x1 = 8.1 , x2 = 2.0时,明天天气分类为1,即明天天气为下雨。
把新点添加到图层,查看可视化效果,图中箭头指向的黑色点就是新点。也可以看出,该点落在有雨的类别中。
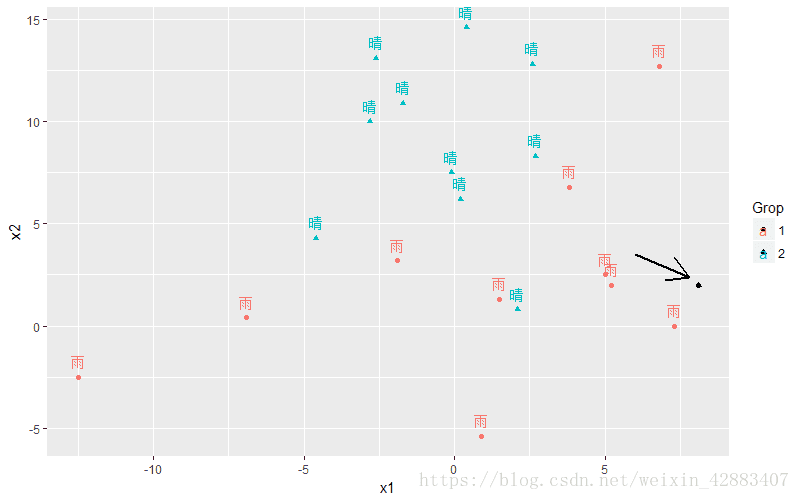
2、距离判别分析
距离判别的基本思想是,根据已知分类的数据,分别计算各类的重心,即各组的均值。距离判别的准则是:对任给的一次观测,若它与第i类的重心距离最近,就认为它来自第i类。通常采用马氏距离进行判别。
设有两总体G1、G2,从第一个总体中抽取n1个样品,从第二个总体中抽取n2个样品,对每个样品测量P个指标。任取一个样品实测指标为X =(x1,x2,…… ,xp)'。分别计算样品X到总体G1、G2的距离D(X , G1)和D(X , G2),按距离最近准则判别归类。即:
在R语言中利用
WeDiBaDis包可以实现加权马氏距离判别分析。
下面距离说明:
从市场上随机抽取了20中牌子的电视机进行调查。按照电视机的质量评分、功能评分、销售价格以及销售情况(共两种,畅销和滞销)进行如下统计(1、表示畅销 , 2、表示滞销)。
现有一新厂商来推销其产品,质量评分8.0,功能评分7.5,售价65百元。该厂商的场景如何?
| 销售状况 | 质量评分 | 功能评分 | 销售价格 |
|---|---|---|---|
| 1 | 8.3 | 4 | 29 |
| 1 | 9.5 | 7 | 68 |
| 1 | 8 | 5 | 39 |
| 1 | 7.4 | 7 | 50 |
| 1 | 8.8 | 6.5 | 55 |
| 1 | 9 | 7.5 | 58 |
| 1 | 7 | 6 | 75 |
| 1 | 9.2 | 8 | 82 |
| 1 | 8 | 7 | 67 |
| 1 | 7.6 | 9 | 90 |
| 1 | 7.2 | 8.5 | 86 |
| 1 | 6.4 | 7 | 53 |
| 1 | 7.3 | 5 | 48 |
| 2 | 6 | 2 | 20 |
| 2 | 6.4 | 4 | 39 |
| 2 | 6.8 | 5 | 48 |
| 2 | 5.2 | 3 | 29 |
| 2 | 5.8 | 3.5 | 32 |
| 2 | 5.5 | 4 | 34 |
| 2 | 6 | 4.5 | 36 |
R语言实现过程:
1)载入数据,分析数据呈现方式
#导入数据
TV_data <- read.table("clipboard" , header = T)
#将分组数据转换成因子
TV_data$G <- as.factor(TV_data$G)
#导入ggplot2包
require(ggplot2)
#建立图层的底层
base_plot <- ggplot(data = TV_data , aes(color = G))
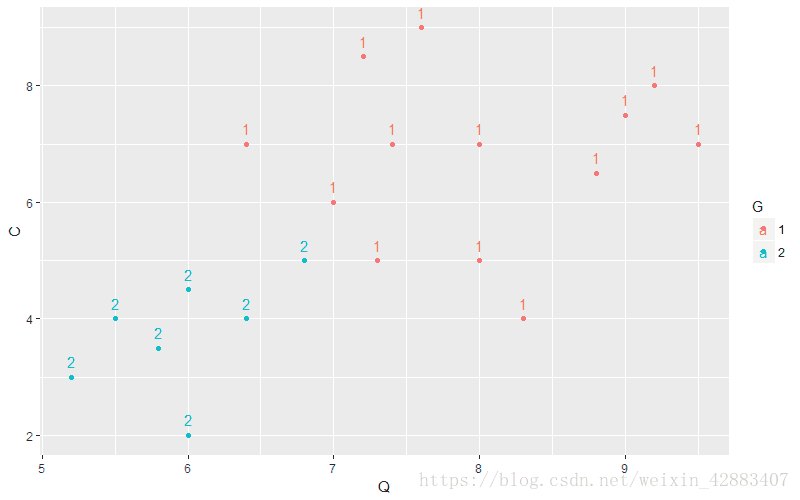
#显示质量评分和功能评分与销售状况的关系
base_plot + geom_point(aes(x = Q , y = C)) + geom_text(aes(x = Q , y = C , label = G) , vjust = -0.8)
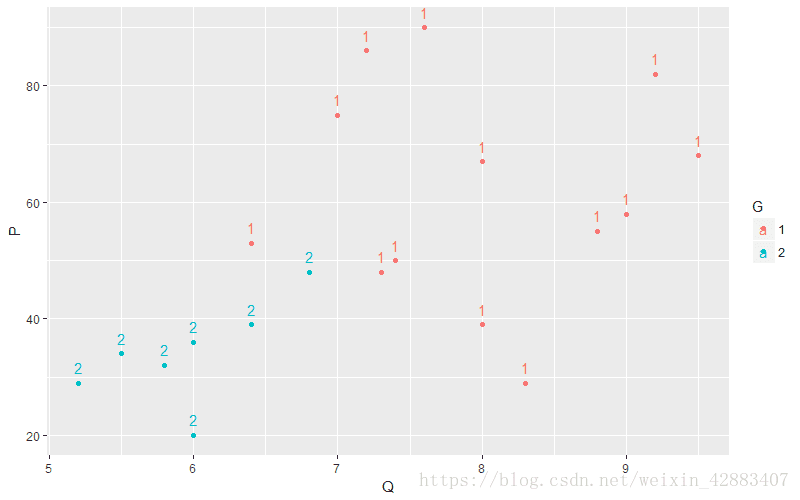
#显示质量评分和销售价格与销售状况的关系
base_plot + geom_point(aes(x = Q , y = P)) + geom_text(aes(x = Q , y = P , label = G) , vjust = -0.8)
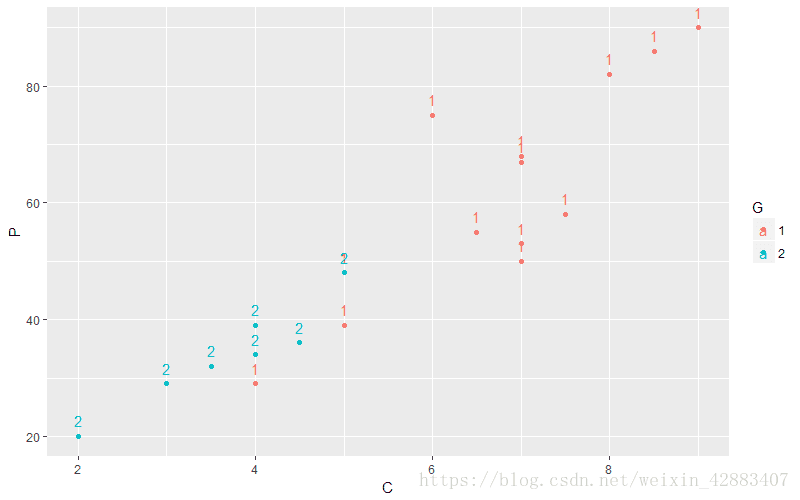
#显示功能评分和销售价格与销售状况的关系
base_plot + geom_point(aes(x = C , y = P)) + geom_text(aes(x = C , y = P , label = G) , vjust = -0.8)2)、导入WeDiBaDis包,建立马氏距离模型。使用WDBdisc ()函数建立模型。
WDBdisc函数结构为:
WDBdisc(data, datatype, classcol, new.ind, distance, type, method)
Data: 一个训练数据矩阵或者训练数据距离矩阵。
Datatype:如果数据是数据矩阵,则datatype = “m”,如果数据是距离矩阵,则datatype = “d”。
Classcol:分类变量所在的列,默认为第一列。
new.ind:为测试数据,可选参数,如果需要测试新数据的话需要加上。
distance: 判别分析采用的距离方法。默认为欧式距离。可选“correlation” , “Bhattacharyya”, “Gower”,“Mahalanobis”,“BrayCurtis”, “Orloci”, “Hellinger”or “Prevosti”。
type: 如果距离为“Gower“距离,则需要该参数。该参数是一个列表。
Method:判别分析采用的方法,为"DB" 或者"WDB",默认为"WDB"。
> #载入程序包
> require(WeDiBaDis)
> #把TV_data转换成数据矩阵
> TV_data_matrix <- as.matrix(TV_data)
> #把矩阵转换成数值型
> TV_data_matrix_1 <- matrix(as.integer(TV_data_matrix) , ncol = 4)
> #进行马氏距离判别分析
> summary(WDBdisc(data = TV_data_matrix_1 , datatype = "m" ,
+ classcol = 1 , distance = "Mahalanobis"))
Discriminant method:
------ Leave-one-out confusion matrix: ------
Predicted
Real 1 2
1 11 2
2 1 6
Total correct classification: 85 %
Generalized squared correlation: 0.4689
Cohen's Kappa coefficient: 0.6808511
Sensitivity for each class:
1 2
84.62 85.71
Predictive value for each class:
1 2
91.67 75.00
Specificity for each class:
1 2
85.71 84.62
F1-score for each class:
1 2
88 80
------ ------ ------ ------ ------ ------
No predicted individuals由此可见训练结果可知,类别1有两个判错的,类别2有一个判错的,判对率为85%。
新数据代入模型,判断新类别的分类。
> #构建新测试数据矩阵
> new_test_data <- matrix(c(8.0 , 7.5 , 65) , nrow = 1)
> #代入训练模型,预测新测试数据分类
> summary(WDBdisc(data = TV_data_matrix_1 , datatype = "m" ,
+ classcol = 1 , new.ind = new_test_data ,
+ distance = "Mahalanobis"))
Discriminant method:
------ Leave-one-out confusion matrix: ------
Predicted
Real 1 2
1 11 2
2 1 6
Total correct classification: 85 %
Generalized squared correlation: 0.4689
Cohen's Kappa coefficient: 0.6808511
Sensitivity for each class:
1 2
84.62 85.71
Predictive value for each class:
1 2
91.67 75.00
Specificity for each class:
1 2
85.71 84.62
F1-score for each class:
1 2
88 80
------ ------ ------ ------ ------ ------
Prediction for new individuals:
Pred. class
1 "1" 由预测结果可知,新类别所属分类为1,即新厂商推广的产品为畅销,新厂商前景比较乐观。
3、二次判别分析
当多总体之间的协方差矩阵不相同时,距离判别函数为非线性形式,一般为二次函数。R语言中用MASS包里的qda()函数来建立模型。
qda()函数书写形式和lda()一样,这里明明同学简单略过。你们可以回头看看线性判别函数lda()书写。
本次还以距离判别的数据为例,用二次判别建立模型,看看模型判对率。
> #二次判别函数构建并查看结果
> (qda_model <- qda(G ~ . , TV_data))
Call:
qda(G ~ ., data = TV_data)
Prior probabilities of groups:
1 2
0.65 0.35
Group means:
Q C P
1 7.976923 6.730769 61.53846
2 5.957143 3.714286 34.00000
> #对训练数据进行模型预测
> predict_TV_data <- predict(qda_model)
> #预测后新的分类
> new_data_grop <- predict_TV_data$class
> #构建原始数据对照表
> cbind(TV_data$G , new_data_grop)
new_data_grop
[1,] 1 1
[2,] 1 1
[3,] 1 1
[4,] 1 1
[5,] 1 1
[6,] 1 1
[7,] 1 1
[8,] 1 1
[9,] 1 1
[10,] 1 1
[11,] 1 1
[12,] 1 1
[13,] 1 1
[14,] 2 2
[15,] 2 2
[16,] 2 2
[17,] 2 2
[18,] 2 2
[19,] 2 2
[20,] 2 2
> #构造混淆矩阵,求出判对率
> tab = table(TV_data$G , new_data_grop)
> sum(diag(prop.table(tab)))
[1] 1由此可见,我们给定的20个样本训练数据训练的模型全部判对。判对率为100%。由此可见应用二次判别比马氏距离判别效果好。
4、Bayes判别分析
前面讲的几种判别分析方法计算简单,结果明确,比较实用。但是存在两个缺点,一是判别方法与总体各自出现的概率大小完全无关;二是判别方法与错判后造成的损失无关,这些都不尽合理。Bayes判别则是很好的考虑了这两个因素而提出的一种判别方法。
我们还以二次判别分析的例子用bayes建模。
1、假设先验概率相等,即q1=q2=1/2,此时判别函数等价于fisher线性判别函数。
> #先验概率相等的bayes判别模型
> (bayes1 <- lda(G ~ . , data = TV_data , prior = c(1 , 1)/2))
Call:
lda(G ~ ., data = TV_data, prior = c(1, 1)/2)
Prior probabilities of groups:
1 2
0.5 0.5
Group means:
Q C P
1 7.976923 6.730769 61.53846
2 5.957143 3.714286 34.00000
Coefficients of linear discriminants:
LD1
Q -0.82211427
C -0.64614217
P 0.01495461
> #对结果进行预测
> bayes1_predict <- predict(bayes1)
> cbind(TV_data$G , bayes1_predict$x , bayes1_predict$class)
LD1
1 1 -0.5866112 1
2 1 -2.9283451 1
3 1 -0.8365730 1
4 1 -1.4710880 1
5 1 -2.2242039 1
6 1 -2.9899051 1
7 1 -0.1222350 1
8 1 -3.1184884 1
9 1 -1.7101283 1
10 1 -2.3296109 1
11 1 -1.7375125 1
12 1 -0.6041099 1
13 1 -0.1265015 1
14 2 2.4619445 2
15 2 1.1249520 2
16 2 0.2845556 2
17 2 2.6080852 2
18 2 1.8366094 2
19 2 1.7900818 2
20 2 1.0858628 22、先验概率不一样,取q1=13/20 , q2=7/20,然后建立bayes判别函数
> #先验概率不相等的bayes判别模型
> (bayes2 <- lda(G~. , data = TV_data , prior = c(13,7)/20))
Call:
lda(G ~ ., data = TV_data, prior = c(13, 7)/20)
Prior probabilities of groups:
1 2
0.65 0.35
Group means:
Q C P
1 7.976923 6.730769 61.53846
2 5.957143 3.714286 34.00000
Coefficients of linear discriminants:
LD1
Q -0.82211427
C -0.64614217
P 0.01495461
> #对结果进行预测
> bayes2_predict <- predict(bayes2)
> cbind(TV_data$G , bayes2_predict$x , bayes2_predict$class)
LD1
1 1 -0.1069501 1
2 1 -2.4486840 1
3 1 -0.3569119 1
4 1 -0.9914270 1
5 1 -1.7445428 1
6 1 -2.5102440 1
7 1 0.3574261 1
8 1 -2.6388274 1
9 1 -1.2304672 1
10 1 -1.8499498 1
11 1 -1.2578515 1
12 1 -0.1244489 1
13 1 0.3531596 1
14 2 2.9416056 2
15 2 1.6046131 2
16 2 0.7642167 2
17 2 3.0877463 2
18 2 2.3162705 2
19 2 2.2697429 2
20 2 1.5655239 2由于我们样本数据少的原因,本结果中无论是先验概率一样还是先验概率不一样的bayes判别都针对本实验完美的进行了判别。判别结果好过马氏距离判别分析。
由于篇幅有限,本文关于判别函数的建立与推到并没有写出,希望大家自己查看资料学习。更多R语言数据分析使用技巧、EXCEL和PPT制作教程明明同学会在博客中相继给大家介绍。
有任何问题请评论区会说明并私信明明同学,明明同学帮助你解决数据分析,PPT制作,论文做图、以及高质量图片处理的难处。