量化投资 –--- 技术篇 (开篇)
量化投资 — 技术篇 (开篇)
基础
一. 前言
本系列主要论述量化投资的基础理论,诸如CAPM、APT、Foundation of Law等。本篇是此系列文章的开篇,主要介绍量化投资的基本概念并引入均值方差模型(Mean-Variance Model)。
量化投资其实就是定量投资,是通过分析一定的数据,在有合理逻辑的支撑下,运用某种策略和模型所进行的具有胜率优势的投资。量化投资技术在海外的发展已有30多年的历史,其投资业绩稳定,市场规模和份额不断扩大、得到了越来越多投资者认可。
量化投资技术所涉及的理论非常广,包括经济学、金融学、概率论和数理统计、优化理论、效用理论还有最近非常流行的机器学习技术等等。例如经济学中的有效市场理论为主动投资环境和信息之间建立了联系;金融学的定价理论可帮助资产定价,还有机器学习技术可以帮助投资者从大量数据中学习有效投资策略和模式。
本系列所指的量化投资是比较广义的概念,包含了资产配置策略和算法交易策略。
二. 几个关键问题
-
成功投资的两个根本原因。
可以控制和引导市场
可以有效预测
一个成功的投资的根本原因无外乎两种:第一种是可以操纵和引导市场,例如著名的金融大鳄索罗斯,这位投资界奇人一般是通过其敏锐的嗅觉洞察某金融市场的不稳定性和漏洞,用大量资金操纵和引导市场为其赚取暴利。
另外一种就是可以有效的预测市场或某个金融资产的走势,投资界的殿堂级人物巴菲特以其价值投资理论享誉全球,主要核心思想就是寻找价格远低于价值的投资,根本上来讲巴菲特认为价格最终会回归其价值,也就是说他可以有效预测该资产的未来价格会远大于当前价格,这个简单有效的方案为其带来了丰厚的投资回报。 -
两个关键技术指标。
-
风险
-
收益
这两点非常直观,投资人一般只关心这两点:可以获得多少收益;需要承担多大风险。对于收益的建模相对容易,例如算数收益率、几何收益率、风险调整收益(Risk-adjusted Return)等。
而风险指的是有多大的可能不能实现预期收益,甚至带来更多的损失。对于风险的建模比较复杂,有收益率的 波动性(Volatility) 和 在险价值(Value at Risk) 等等。更多实践者再用收益波动性,即收益的标准差来定义风险,笔者在后续系列中还会深入讨论风险和收益指标。
-
-
量化投资依赖的两个要素
-
信息
-
模型
有效市场理论(Effective Market Theory) 把市场环境分为三种:弱有效、半强有效和强有效。它告诉我们,在弱有效市场环境下,不可能从资产的历史价格上获得稳定正超额收益;在半强有效市场下,不可能通过历史价格和公开信息而获得稳定正超额收益;最后,在强有效市场环境下,价格数据包含了所有信息,任何人都不可能通过任何信息而获得稳定正超额收益。
所以对于量化投资而言,采用最优模型且配合高效的信息使用率是其成功的关键要素。
-
三. 均值方差模型(Mean-Variance Model)
-
背景知识
在引入均值方差模型之前,我们需要考虑一个问题:如何评价一个投资好还是不好。前文中我们说过风险和收益是投资者所关心的核心指标,不同的投资者有不同的风险偏好。我们首先假设所有投资者都是厌恶风险的,也就是说在同样的收益率下,投资者偏好风险低的投资组合。所以投资者之所以会选择一个高风险的资产,一定是该资产的期望收益较高;相反的,投资者如果想要获得更高的期望收益,也需要承担更大的风险。这一点是基本符合客观事实的。
所有投资者都是在收益和风险之间进行权衡,但在同样的风险水平下,如何追求最大收益呢?或者在同样的期望收益下,如何使风险最小化呢?这个就是均值方差模型或均值方差分析,即现代投资组合理论(Modern Portfolio Theory) 来解决的问题。
设某投资组合 p p p,其收益为 R p R_p Rp, R i R_i Ri为组合中的第 i i i个资产, w i w_i wi为对应的权重,也就是该资产的资金在整个组合中所占的比例。
E ( R p ) = ∑ i w i ∗ R i E(R_p)=\sum_iw_i*R_i E(Rp)=∑iwi∗Ri (1.1)
R p R_p Rp的期望收益等于各个资产 i i i的收益乘以该资产的权重的和。
σ p 2 = W T Σ W \sigma_p^2=W^T\Sigma{W} σp2=WTΣW (1.2)
σ p = σ p 2 \sigma_p=\sqrt{\sigma_p^2} σp=σp2 (1.3)
(1,2)式中的 Σ \Sigma Σ 是资产的收益的协方差矩阵, σ p 2 \sigma_p^2 σp2是投资组合收益的方差,而 σ p \sigma_p σp就是收益标准差,即波动率。本节中我们以波动率来定义风险。接下来,我们来看一下MPT理论中所揭示的如何通过多元化来降低风险的。
假设我们的投资符合中有两个资产A、B,其组合收益为:
E ( R p ) = w A ∗ E ( R A ) + w B ∗ E ( R B ) E(R_p)=w_A*E(R_A)+w_B*E(R_B) E(Rp)=wA∗E(RA)+wB∗E(RB) (1.4)
其方差:
σ p 2 = w A 2 σ A 2 + w B 2 σ B 2 + 2 w A w B σ A σ B ρ A B \sigma_p^2=w_A^2\sigma_A^2+w_B^2\sigma_B^2+2w_Aw_B\sigma_A\sigma_B\rho_{AB} σp2=wA2σA2+wB2σB2+2wAwBσAσBρAB (1.5)
我们可以看出如果降低两个资产的相关系数 ρ A B \rho_{AB} ρAB, 就可以降低其方差,从而降低风险。
-
有效前沿
通过引入期望效用理论,我们可以为这个问题建立模型,认为投资优化的目标为最小化下式得到有效前沿(Effective Frontier):
W Σ W T − λ R T W W\Sigma{W^T}-\lambda{R^T}W WΣWT−λRTW (1.6)
λ \lambda λ是指风险容忍度, λ > 0 \lambda>0 λ>0。上式中第一项代表风险,第二项代表收益。最小化(1.6)式代表风险尽量小而收益尽可能大。 R T R^T RT代表多个资产的收益向量, W W W是投资组合中各个资产的权重向量。
图一中包含了MPT理论的核心:有效前沿(Effective Frontier)
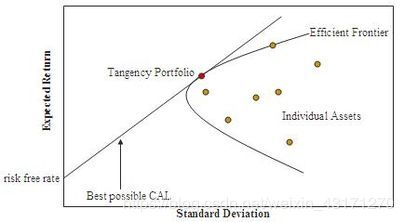
图一. 有效前沿
上图中的横坐标是标准差,代表风险;纵坐标是期望收益;纵坐标轴上有无风险利率点(Risk Free Rate)。途中的曲线是双曲线,其上沿就是有效前沿。图中的直线为CAL(Capital Allocation Line),其和有效前沿的切点称为Tangency Portfolio,即途中的红点,而图中的黄点代表这各个独立资产。下面我们来详细阐述一下这个经典理论。
(1.6)式表示了风险和收益的权衡,我们可以这样理解:在给定收益 R T W R^TW RTW的情况下,最小化风险 W Σ W T W\Sigma{W^T} WΣWT,或者在给定风险的情况下最大化收益。该问题转化为有约束的极值问题,应用拉格朗日乘子很容易求解。随这风险水平和收益水平的移动,我们可以得到有效前沿。有效前沿中的每个点都代表着在给定风险水平下的收益最大值或者给定收益的情况下风险最小值。注意:这里的有效前沿是在不包括无风险利率的情况下产生的。
切点组合(Tangency Portfolio)代表着收益与风险比最大的点。CAL的截距就是无风险利率,实践中经常用国债或者银行定期存款利率等超低风险的资产来代表。在无风险利率点(RF)和切点组合(TP)中的所有点都可以通过RF和TP的线性组合来达到,而在TP右上方的点需要通过杠杆操作即以RF借款(负权重)投资TP来得到。因此我们可以引出共同基金定理(One Mutual Fund Theorem):CAL上的所有点都可以通过RF和TP的线性组合来得到。在存在无风险利率的情况下,有效前沿应该是CAL在TP右上侧的那一部分。公式如下:
E ( R C ) = R F + σ C E ( R p ) − R F σ P E(R_C)=R_F+\sigma_C\frac{E(R_p)-R_F}{\sigma_P} E(RC)=RF+σCσPE(Rp)−RF (1.7)
其中, R C R_C RC是组合收益, σ C \sigma_C σC是组合收益标准差, R P R_P RP是Tangency Portfolio的收益, σ P \sigma_P σP是其标准差, R F R_F RF是无风险收益。
如果每个投资着对每个资产的收益概率分布的人是都是一样的,且都在以MVO模型进行优化,那么最终每个投资者都会收敛于一个基金:市场组合收益。
-
两共同基金定理(Two Mutual Fund Theorem)
有效前沿上的投资组合可以通过线性组合任意两个在有效前沿上的其他投资组合而得到。意思是说均值方差有效的投资组合可以由任意其他均值方差有效的投资组合组合而获得。如果目标组合是在两个组合之间,那么两个组合都是正权重,否则,可以通过做空其中一个组合来得到。
四. 结束语
关于MPT的讨论其实还没有结束,在后续系列中我们还会涉及这个话题。这里有些地方需要引起我们注意:
-
MVO模型对上行波动和下行波动赋予了同样的权重。
这一点显然不太符合人们的直观认识,因为相比于下行波动,投资者肯定会青睐于上行波动。
-
MVO的分析中,假设资产的收益、波动性和相关性都是已知的。
MVO分析其实是假设各个资产的收益,波动性和相关性都是已知的,但这一点在实际实现中显然无法做到。我们只能去尽可能估算这些参数,但是不可能非常精确。如何有效的降低估算误差,我们将会在后续系列中陆续介绍。
最后MVO分析是比较期望收益是正态分布的,原因之一是正态分布是完全由均值和方差,也就是其一阶和二阶统计量来完全确定的分布之一。其他原因我们将在期望效用理论介绍中看到相关讨论。