翻译：图像拼接

0 简介

图像拼接是将同一场景的多个重叠图像拼接成较大的图像的一种方法，在医学成像、计算机视觉、卫星数据、军事目标自动识别等领域具有重要意义。图像拼接的输出是两个输入图像的并集。通常用到五个步骤：

Created with Raphaël 2.2.0 输入图像 特征提取Feature Extraction 图像配准 Image Registration 用RANSAC计算单应矩阵H 变形和融合 ImageWraping and Blending 输出图像

特征提取 Feature Extraction：在所有输入图像中检测特征点
图像配准 Image Registration：建立了图像之间的几何对应关系，使它们可以在一个共同的参照系中进行变换、比较和分析。
大致可以分为以下几个类

1. 直接使用图像的像素值的算法,例如,correlation methods
2. 在频域处理的算法,例如,基于快速傅里叶变换(FFT-based)方法;
3. 低水平特征的算法low level features,通常用到边缘和角点，例如，基于特征的方法,
4. 高水平特征的算法high-level features,通常用到图像物体重叠部分，特征关系，例如，图论方法（Graph-theoretic methods）

图像变形 Warping：
图像变形是指将其中一幅图像的图像重投影，并将图像放置在更大的画布上。
图像融合 Blending
图像融合是通过改变边界附近的图像灰度级，去除这些缝隙，创建混合图像，从而在图像之间实现平滑过渡。混合模式(Blend modes)用于将两层融合到一起。

特征点提取

特征是要匹配的两个输入图像中的元素，它们是在图像块的内部。这些图像块是图像中的像素组。对输入图像进行Patch匹配。具体解释如下: 如下图所示，fig1和fig2给出了一个很好的patch匹配，因为fig2中有一个patch看起来和fig1中的patch非常相似。当我们考虑到fig3和fig4时，这里的patch并不匹配，因为fig4中有很多类似的patch，它们看起来与fig3中的patch很相似。由于像素强度很相近，所以无法进行精确的特征匹配，

为了给图像对提供更好的特征匹配，采用角点匹配，进行定量测量。角点是很好的匹配特性。在视点变化时，角点特征是稳定的。此外，角点的邻域具有强度突变。利用角点检测算法对图像进行角点检测。角点检测算法有Harris角点检测算法、SIFT特征点检测算法((Scale Invariant Feature Transform),FAST算法角点检测算法，SURF特征点检测算法(Speeded-up robust feature)

Harris角点检测算法

Harris算法是一种基于Moravec算法的点特征提取算法。1988年C. Harris 和 M.J Stephens设计了一种图像局部检测窗口。通过在不同的方向上移动少量窗口，可以确定强度的平均变化。我们可以通过观察小窗口内的强度值很容易地识别角点。在移动窗口时，平坦区域在所有方向上均不会显示强度的变化。边缘区域在沿边缘方向强度不会发生变化。对于角点，则在各个方向上产生显著强度变化。Harris角点探测器给出了一种检测平坦区域、边缘和角点的数学方法。Harris检测的特征较多，具有旋转不变性和尺度变异性。位移$[u,v]$下的强度变化:$$E(u,v)=\sum _{x,y}w(x,y)[I(x+u,y+v)-I(x,y){]}^2$$其中，$w(x,y)$是窗口函数，$I(x+u,y+v)$是移动后的强度，$I(x,y)$是单个像素位置的强度。

Harris角点检测算法如下：

1. 对图像中的每个像素点$(x,y)$计算自相关矩阵$M$（autocorrelation matrix M）:
   $$M=\sum _{x,y}\left[\begin{array}{cc}{I}_x^2& I_x{I}_y\\ I_x{I}_y& I_y^2\end{array}\right]$$其中$I_x,I_y$是$I(x,y)$的偏导数
2. 对图像中的每个像素点做高斯滤波，获得新的矩阵$M$，离散二维零均值高斯函数为$$Gauss=exp(-u^2+v^2)/2{\delta }^2$$
3. 计算每个像素点(x,y)的角点度量，得到$$R=Det(M)-k\ast trace(M)$$，$k$ 的范围是$0.04\le k\le 0.06$。
4. 选择局部最大值点。Harris方法认为特征点与局部最大兴趣点的像素值对应。
5. 设置阈值T，检测角点。如果 $R$ 的局部最大值高于阈值$T$，那么此点为角点。

SIFT角点检测算法

SIFT算法是尺度不变的特征点检测算法，可用于识别其他图像中的相似目标。SIFT的图像特征表示为关键点描述符（key-point-descriptors）。在检查图像匹配时，将两组关键点描述符作为输入提供给最近邻搜索(Nearest Neighbor Search，NNS)，并生成一个紧密匹配的关键点描述符（matching key-point-descriptors）。

SIFT的计算分为四个阶段:

1. 尺度空间构造（Scale-space construction）
2. 尺度空间极值检测(Scale-space extrema detection)
3. 关键点定位(key-point localization)
4. 方向分配(orientation assignment)和关键点描述符定义(defining key-point descriptors)

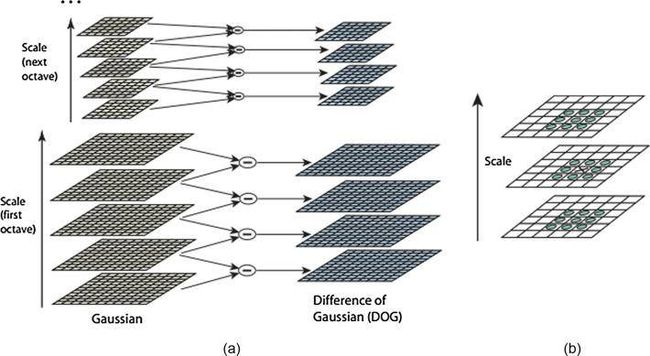
第一阶段确定潜在的兴趣点。它利用高斯函数的差分(difference of Gaussian function,DOG)搜索所有尺度和图像位置。第一阶段中发现的所有兴趣点的location和scale是确定的。根据关键点的稳定性来选择关键点。一个稳定的关键点能够抵抗图像失真。在方向分配环节，SIFT算法计算稳定关键点周围梯度的方向。根据局部图像梯度方向，为每个关键点分配一个或多个方向。对于一组输入帧，SIFT提取特征。图像匹配使用Best Bin First(BBF)算法来估计输入帧之间的初始匹配点。为了去除不属于重叠区域的不需要的角，使用RANSAC算法。它删除图像对中的错误匹配。通过定义帧的大小、长度和宽度来实现帧的重投影。最后进行拼接，得到最终的输出拼接图像。在拼接时，检查场景每帧中的每个像素是否属于扭曲的第二帧。如果是，则为该像素分配来自第一帧的对应像素的值。SIFT算法既具有旋转不变性，又具有尺度不变性。SIFT非常适合于高分辨率图像中的目标检测。它是一种鲁棒的图像比较算法，虽然速度较慢。SIFT算法的运行时间很大，因为比较两幅图像需要更多的时间。

FAST 算法

FAST是Trajkovic和Hedley在1998年创建的角点检测算法。对于FAST，角点的检测优于边缘检测，因为角点有二维强度变化，容易从邻近点中区分出来。适用于实时图像处理应用程序。

FAST角点探测器应该满足以下要求：

1. 检测到的位置要一致，对噪声变化不敏感，对同一场景的多幅图像不能移动。
2. 准确;检测到的角点应该尽可能接近正确的位置。
3. 速度;角落探测器应该足够快。

原理：首先围绕一个候选角点选择16个像素点。如果其中有n（n一般为12）个连续的像素都比候选角点加上一个阈值要高，或者比候选角点减去一个阈值要低，那么此点即为角点（如图4所示）

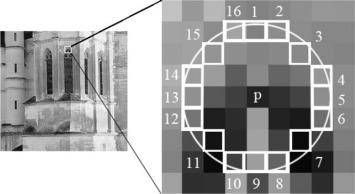
为了加快FAST算法的速度，通常会使用角点响应函数（ corner response function, CRF)。该函数根据局部邻域的图像强度给出角点强度的数值。
对图像进行CRF计算，并将CRF的局部最大值作为角点，采用多网格（multi-grid）技术提高了算法的计算速度，并对检测到的假角点进行了抑制。FAST是一种精确、快速的算法，具有良好的定位(位置精度)和较高的点可靠性。FAST的角点检测的算法难点在于最佳阈值的选择。

SURF算法

Speed-up Robust Feature(SURF)角点探测器采用三个特征检测步骤;检测(Detection)、描述(Description)、匹配(Matching)，SURF通过考虑被检测点的质量，加快了位移的检测过程。它更注重加快匹配步骤。使用Hessian矩阵和低维描述符来显著提高匹配速度。SURF在计算机视觉社区中得到了广泛的应用。SURF在不变特征定位上十分有效和鲁棒

图像配准

在特征点被检测出来之后，我们需要以某种方式将它们关联起来,可以通过NCC或者SDD（Sum of Squared Difference）方法来确定其对应关系。

归一化互相关（normalized cross correlation，NCC）

互相关的工作原理是分析第一幅图像中每个点周围的像素窗口，并将它们与第二幅图像中每个点周围的像素窗口关联起来。将双向相关性最大的点作为对应的对。

基于图像强度值计算在两个图像中的每个位移（shifts）的“窗口”之间的相似性

$$NCC(u)=\frac{{\sum }_i[I_1(x_i)-\overline{I_1}][I_2(x_i+u)-\overline{I_2}]}{\sqrt{{\sum }_i[I_1(x_i)-\overline{I_1}{]}^2[I_2(x_i+u)-\overline{I_2}{]}^2}}$$
其中，$\overline{I_1},\overline{I_2}是窗口的平均值图像$
$\overline{I_1}=\frac{1}{N}{\sum }_i{I}_1(x_i)$
$\overline{I_2}=\frac{1}{N}{\sum }_i{I}_2(x_i+u)$
$I_1(x,y)$和$I_2(x,y)$分别是两张图片。$x_i=(x_i,y_i)$ 是窗口的像素坐标，$u=(u,v)$ 是通过NCC系数计算出的位移或偏移。NCC系数的范围为$[-1,1]$。 NCC峰值相对应的位移参数表示两个图像之间的几何变换。此方法的优点是计算简单，但是速度特别慢。此外，此类算法要求源图像之间必须有显著的重叠。

互信息（Mutual Information, MI）

互信息测量基于两个图像之间共享信息数量的相似性。

两个图像$I_1(X,Y)$与$I_2(X,Y)$之间的MI以熵表示：

$$MI(I_1,I_2)=E(I_1)+E(I_2)-E(I_1,I_2)$$
其中，$E(I_1)$ 和$E(I_2)$分别是$I_1(x,y)$和$I_2(x,y)$的熵。$E(I_1,I_2)$表示两个图像之间的联合熵。
$$E(I_1)=-\sum _g{p}_{I1}(g)log(p_{I1}(g))$$
$g$是$I_1(x,y)$可能的灰度值，$p_{I1}(g)$是$g$的概率分布函数
$$E(I1,I2)=-\sum _{g,h}{p}_{I_1,I_2}(g,h)log(p_{I_1,I_2}(g,h))$$

然而，从图中我们可以看到，许多点被错误地关联在一起。

计算单应矩阵

单应矩阵估计是图像拼接的第三步。在单应矩阵估计中，不属于重叠区域的不需要的角被删除。采用RANSAC算法进行单应。

随机样本一致算法RANSAC(random sample consensus)

RANSAC算法从可能含有异常值的观测数据集中拟合数学模型，是一种鲁棒参数估计的迭代方法。该算法是不确定性的，因为它只在一定的概率下产生一个合理的结果，随着执行更多的迭代，这个概率会增加。RANSAC算法用于在存在大量可用数据外行的情况下以鲁棒的方式拟合模型。RANSAC算法在计算机视觉中有许多应用。

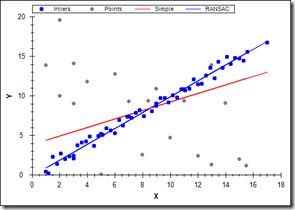
RANSAC原理

从数据集中随机选取一组数据并认为是有效数据（内点）来确定待定参数模型，以此模型测试数据集中的所有数据，满足该模型的数据成为内点，反之为外点（通常为噪声、错误测量或不正确数据的点），迭代执行，直到某一个参数模型得到的内点数最大，则该模型为最优模型。
考虑如下假设:

1. 参数可以从N个数据项中估计。
2. 可用的数据项总共是M。
3. 随机选择的数据项成为好模型的一部分的概率为$P_g$。
4. 如果存在一个很好的拟合，那么算法在没有找到一个很好的拟合的情况下退出的概率是$P_{fail}$。

RANSAC步骤

1. 随机选取N个数据（3个点对）
2. 估计参数x（计算变换矩阵H）
3. 根于使用者设定的阈值，找到M中合适该模型向量x的的数据对总数量K（ 计算每个匹配点经过变换矩阵后到对应匹配点的距离，根据预先设定的阈值将匹配点集合分为内点和外点，如果内点足够多，则H足够合理，用所有内点重新估计H）。
4. 如果符合的数量K足够大，则接受该模型并退出
5. 重复1-4步骤 L次
6. 到这一步退出

K有多大取决于我们认为属于合适结构的数据的百分比以及图像中有多少结构。如果存在多个结构，则在成功拟合后，删除拟合数据并重做RANSAC。

迭代次数L可以用如下公式计算：
$P_{fail}=L连续失败的概率$
$P_{fail}=(给定试验失败的概率)L$
$P_{fail}=(1-给定试验成功的概率)L$
$P_{fail}=(1-(随机数据项符合模型的概率)N)L$
$P_{fail}=(1-(Pg{)}^N{)}^L$
$L=log(P_{fail})/log(1-(Pg)N)$

优点：可以robust地估计模型参数
缺点：迭代次数无上限，设置的迭代次数会影响算法时间复杂度和精确程度，并且需要预设阈值

在执行RANSAC之后，我们只能在图像中看到正确的匹配，因为RANSAC找到了一个与大多数点相关的单应矩阵，并将不正确的匹配作为异常值丢弃

单应矩阵（Homography）

有了两组相关点，接下来就需要建立两组点的转换关系，也就是图像变换关系。单应性是两个空间之间的映射，常用于表示同一场景的两个图像之间的对应关系，可以匹配大部分相关的特征点，并且能实现图像投影，使一张图通过投影和另一张图实现大面积的重合。

设2个图像的匹配点分别是$X=[x,y{]}^T$,$X^{\prime }=[x^{\prime },y^{\prime }{]}^T$，则必须满足公式：
$$X^{\prime }=HX$$且由于两向量共线，所以$$X^{\prime }\times HX=0$$其中，$H$ 为8参数的变换矩阵，可知四点确定一个H
$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right)=\left(\begin{array}{ccc}{h}_{11}& h_{12}& h_{13}\\ h_{21}& h_{22}& h_{23}\\ h_{31}& h_{32}& 1\end{array}\right)\left(\begin{array}{c}x\\ y\\ 1\end{array}\right)$$

令 $$h=(h11:h12:h13:h21:h22:h23:h31:h32:h33)T$$则有
$$Bh=0$$N个点对给出2N个线性约束。
$$\underset{h}{\min }║Bh{║}^2，║h║=1$$
用RANSAC方法估算H：

1. 首先检测两边图像的角点
2. 在角点之间应用方差归一化相关，收集相关性足够高的对，形成一组候选匹配。
3. 选择四个点，计算H
4. 选择与单应性一致的配对。如果对于某些阈值:Dist(Hp、q) <ε，则点对(p, q)被认为与单应性H一致
5. 重复34步，直到足够多的点对满足H
6. 使用所有满足条件的点对，通过公式重新计算H

图像变形和融合

最后一步是将所有输入图像变形并融合到一个符合的输出图像中。基本上，我们可以简单地将所有输入的图像变形到一个平面上，这个平面名为复合全景平面。

图像变形步骤

1. 首先计算每个输入图像的变形图像坐标范围，得到输出图像大小，可以很容易地通过映射每个源图像的四个角并且计算坐标(x,y)的最小值和最大值确定输出图像的大小。最后，需要计算指定参考图像原点相对于输出全景图的偏移量的偏移量x_offset和偏移量y_offset。
2. 下一步是使用上面所述的反向变形，将每个输入图像的像素映射到参考图像定义的平面上，分别执行点的正向变形和反向变形。

平滑过渡（transition smoothing）图像融合方法包括 羽化（feathering）， 金字塔（pyramid）， 梯度（gradient）

图形融合

最后一步是在重叠区域融合像素颜色，以避免接缝。最简单的可用形式是使用羽化（feathering），它使用加权平均颜色值融合重叠的像素。我们通常使用alpha因子，通常称为alpha通道，它在中心像素处的值为1，在与边界像素线性递减后变为0。当输出拼接图像中至少有两幅重叠图像时，我们将使用如下的alpha值来计算其中一个像素处的颜色：
假设两个图像 $I_1,I_2$,在输出图像中重叠；每个像素点$(x,y)$在图像$I_i(x,y)=(\alpha iR,\alpha iG,\alpha iB,\alpha j,)$，其中（R,G,B）是像素的颜色值，我们将在缝合后的输出图像中计算(x, y)的像素值：
$$[(\alpha 1R,\alpha 1G,\alpha 1B,\alpha 1)+(\alpha 2R,\alpha 2G,\alpha 2B,\alpha 2)]/(\alpha 1+\alpha 2)$$.

参考

1. OpenCV探索之路（二十四）图像拼接和图像融合技术

2. Debabrata Ghosh,Naima Kaabouch. A survey on image mosaicing techniques[J]. Journal of Visual Communication and Image Representation,2016,34.地址

3. 图像拼接综述