查找与排序(LeetCode+剑指 )
二分查找必须为有序序列!
理解下面2道题,可很好掌握大顶推,小顶推。
❀❀❀
规律(理解):
求最小的k个数--> 大顶堆(堆里的元素都比它小)
求最大的k个数--> 小顶堆(堆里的元素都比它大)
(1)剑指40. 最小的k个数
这道题LeetCode有问题,我在牛客提交。
输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
示例 1:
输入:arr = [3,2,1], k = 2
输出:[1,2] 或者 [2,1]
示例 2:
输入:arr = [0,1,2,1], k = 1
输出:[0]
法1:暴力
class Solution {
public:
vector<int> getLeastNumbers(vector<int>& arr, int k) {
vector<int> res;
if(arr.empty()||k>arr.size())
return res;
sort(arr.begin(),arr.end());
for(int i=0;i<k;i++){
res.push_back(arr[i]);
}
return res;
}
};
法2:堆,维护一个大顶堆。当外界元素小于堆顶元素时,堆顶元素更新为当前外界元素
为什么不通过,我疯了
后来看到法三,受启发,只因一个输入的初始条件不对,我说呢,明明每个函数都正确,为什么就通不过,啊啊啊
只因这个条件没有判断全!! if(len<=0||k>len||k<=0) return vector<int>();
class Solution {
public:
vector<int> GetLeastNumbers_Solution(vector<int> arr, int k) {
int len=arr.size();
if(len<=0||k>len||k<=0) return vector<int>();
vector<int> res(arr.begin(),arr.begin()+k);
//vector res;
//for (int i = 0; i < k; i++) res.push_back(arr[i]);
for(int i=0; i<k; i++){
//heap[i] = arr[i];
heapInsert(res, i);//建立大堆
}
for (int i = k; i < arr.size(); i++){
if(arr[i] < res[0]){
res[0] = arr[i];
heapify(res, 0, k);
}
}
return res;
}
private:
void heapInsert(vector<int>& arr, int index) {
while (arr[index] > arr[(index - 1) / 2]) {//如果比当前父节点位置大,就和父位置交换
swap(arr, index, (index - 1) / 2);
index = (index - 1)/ 2;// index往上跑
}
}
void heapify(vector<int>& arr, int index, int size) {
int left = index * 2 + 1;
while (left < size) {
int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;//选出左右孩子中较大的那个
largest = arr[largest] > arr[index] ? largest : index;
if (largest == index) {
break;
}
swap(arr, largest, index);
index = largest;
left = index * 2 + 1;
}
}
void swap(vector<int>& arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
};
法3:大堆,(用的C++库函数)
class Solution {
public:
vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {
int len=input.size();
//if(len<=0||k>len) return vector();
if(len<=0||k>len||k<=0) return vector<int>();//这个条件很重要,没有就报错
vector<int> res(input.begin(),input.begin()+k);
//vector res;
//for (int i = 0; i < k; i++) res.push_back(input[i]);
//建堆
make_heap(res.begin(),res.end());
for(int i=k;i<len;i++)
{
if(input[i]<res[0])
{
//先pop,然后在容器中删除
pop_heap(res.begin(),res.end());
res.pop_back();
//先在容器中加入,再push
res.push_back(input[i]);
push_heap(res.begin(),res.end());
}
}
//使其从小到大输出
sort_heap(res.begin(),res.end());
return res;
}
};
法4:快排 partition
因为pivot指向的位置,它的左边一定是比pivot小的数,所以一直执行partition,直到pivot到达k了(实际是k-1,因为pivot是下标),就停止。
class Solution {
public:
vector<int> GetLeastNumbers_Solution(vector<int> arr, int k) {
if(arr.empty() || k<=0 || k > arr.size()) return vector<int>(); //处理异常输入
int left = 0;
int right = arr.size() - 1; // 注意
while(left <= right) {//类似二分查找法
int mid = partition(arr,left,right);
if(mid == k-1) ///如果mid==k-1,说明,mid已到达k-1的位置,此时mid前面的数都小于mid
break;
else if (mid < k-1) //说明mid应该在右边,所以重新再右半段找。
left = mid + 1; // 注意
else if (mid > k-1)
right = mid - 1; // 注意
}
vector<int> result(arr.begin(), arr.begin()+k); //构造结果向量
return result;
}
//不要被误导,下面函数中的left,right是局部变量,和上面的没关系。
int partition(vector<int>& arr,int left,int right){
int pivot=arr[left];
while(left<right){
while(arr[right]>=pivot && left<right) right--;
arr[left]=arr[right];//这覆盖可以,写swap函数交换也可以,道理是一样的
while(arr[left]<=pivot && left<right) left++;
arr[right]=arr[left];
}
arr[left]=pivot;
return left;
}
};
❀❀❀
(2)215. 数组中的第K个最大元素
法1,思路:快排partition
**方法一:基于partition函数(快排中有用到,stl中也有,但是还是自己实现较好)
多次partition直到枢轴位置为k即可
缺点:会改变输入数组的元素位置
**
和上题类似,只不过从大到小排
在未排序的数组中找到第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
class Solution {
public:
int findKthLargest(vector<int>& arr, int k) {
if(arr.empty() || k<=0 || k > arr.size()) return 0; //处理异常输入
int left = 0;
int right = arr.size() - 1; // 注意
int mid;
while(left <= right) {//类似二分查找法
mid = partition(arr,left,right);
if (mid < k-1)
left = mid + 1; // 注意
else if (mid > k-1)
right = mid - 1; // 注意
else break;
}
return arr[mid]; //服了,在while循环里return还报错,我认为是编译器原因
}
int partition(vector<int>& arr,int left,int right){
int pivot=arr[left];
while(left<right){
//改造为从大到小partition,注意符号的变化
while(arr[right]<=pivot && left<right) right--;
arr[left]=arr[right];//这覆盖可以,写swap函数交换也可以,道理是一样的
while(arr[left]>=pivot && left<right) left++;
arr[right]=arr[left];
}
arr[left]=pivot;
return left;
}
};
法2,改进:维护一个大小为k的小顶堆,扫描输入数据,不断更新小顶堆的内容,最后堆顶元素即可n个数中第k大的数
再理解:应该是建一个只能存K个数字的小顶堆,超过K时候,每加进来一个,堆顶就要弹出一个。数组遍历完,最终堆顶的元素就是第K大的(堆里其他元素都比他还要大)。
每次堆调整平均时间复杂度为O(logk),共n次调整,故时间复杂度为O(nlogk)
O(nlogk), O(k)
万变不离其中,说白了就是大堆变小堆的灵活运用,改的时候注意3个地方。
class Solution {
public:
int findKthLargest(vector<int>& arr, int k) {
if(arr.empty() || k<=0 || k > arr.size()) return 0; //处理异常输入
vector<int> res(arr.begin(),arr.begin()+k);
//vector res;
//for (int i = 0; i < k; i++) res.push_back(arr[i]);
for(int i=0; i<k; i++){
heapInsert(res, i);//建立小顶堆
}
for (int i = k; i < arr.size(); i++){
if(arr[i] > res[0]){ //注意,第一个改的地方,比堆顶元素大的需要放进来
res[0] = arr[i];
heapify(res, 0, k);
}
}
return res[0];
}
private:
void heapInsert(vector<int>& arr, int index) {
while (arr[index] < arr[(index - 1) / 2]) {//第二个改的地方,构建小顶推的过程
swap(arr, index, (index - 1) / 2);
index = (index - 1)/ 2;// index往上跑
}
}
void heapify(vector<int>& arr, int index, int size) {
int left = index * 2 + 1;
while (left < size) {
int largest = left + 1 < size && arr[left + 1] < arr[left] ? left + 1 : left;//第三个改地方,找出三者之间最小的
largest = arr[largest] < arr[index] ? largest : index;
if (largest == index) {
break;
}
swap(arr, largest, index);
index = largest;
left = index * 2 + 1;
}
}
void swap(vector<int>& arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
};
❀❀❀
(3)面试题41. 数据流中的中位数【hard】(LC295)
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
例如,
[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。
用优先队列模拟大小堆
/*
1 2 3 4 [5] + [6] 7 8 9 10
大顶堆 + 小顶堆
方法一:用两个堆(stl中的priority_queue)
过程:用于一个大顶堆实现左边容器,小顶堆实现右边容器,根据左边最大数与右边最小数得到中位数
(1) 平均分配
(2) 还要保证大顶堆中所有数据小于小顶堆中元素,比较新数据与大顶堆和小顶堆堆顶元素就知道该放到哪里
插入O(logn) 得到中位数O(1),空间复杂度O(n)
*/
class MedianFinder {
public:
/** initialize your data structure here. */
MedianFinder() {
}
void addNum(int num) {
if(maxheap.empty() || num<maxheap.top()) {
maxheap.push(num);
}
else minheap.push(num);
//因为最后要求取中位数,所以必须时刻保持两边长度一致,或者左边比右边多一
if(maxheap.size() < minheap.size())
{
maxheap.push(minheap.top());
minheap.pop();
}
else if(maxheap.size() > minheap.size() + 1){//取等号时,左边比右边多一,这时左边不能再多了
minheap.push(maxheap.top());
maxheap.pop();
}
}
double findMedian() {
return (maxheap.size()>minheap.size()) ? maxheap.top() : (maxheap.top() + minheap.top())*0.5; //奇数时,返回中间元素,偶数时,返回中间两个数的平均数,注意浮点数的处理
}
private:
priority_queue<int> maxheap; //stl中默认为大顶堆
priority_queue<int, vector<int>, greater<int>> minheap; //小顶堆
};
❀❀❀
(4)面试题11. 旋转数组的最小数字(LC154)
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。
例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转,该数组的最小值为1。
示例 1:
输入:[3,4,5,1,2]
输出:1
示例 2:
输入:[2,2,2,0,1]
输出:0
思路
该题减治的思想是:通过排除不可能是最小值元素,进而缩小范围。当我们拿中间的数和最右边的数相比时,有三种情况:
1. 中间的数比右边的大,那么中间数不可能是最小的数,最小的数只可能出现在中间数的后面,改left = mid + 1缩小区间
2. 中间的数和右边的小,那么右边的数不可能是中位数,此时,中间的数可能是最小的数,改right = mid 缩小区间
3. 中间的数和右边相等,例如[3,3,3,1,3]此时中间的数和最右边的数都为3,可以知道的是,此时我们可以排除最右边的数,改区间为right = right - 1
class Solution {
public:
int minArray(vector<int>& numbers) {
int i = 0, j = numbers.size() - 1;
//答案是while (i < j) ,但我觉的“<=”对
//后来发现都可以,举个例子[3,4,5,1]
while (i <= j) {
int m = (i + j) / 2;
if (numbers[m] > numbers[j]) i = m + 1;
else if (numbers[m] < numbers[j]) j = m;
else j--;
}
return numbers[i];
}
};
❀❀❀
(5)33. 搜索旋转排序数组(不存在重复数字)
二分查找各种等号是关键
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
搜索一个给定的目标值,如果数组中存在这个目标值,则返回它的索引,否则返回 -1 。
你可以假设数组中不存在重复的元素。
你的算法时间复杂度必须是 O(log n) 级别。
示例 1:
输入: nums = [4,5,6,7,0,1,2], target = 0
输出: 4
示例 2:
输入: nums = [4,5,6,7,0,1,2], target = 3
输出: -1
思路:二分查找,先找有序范围,再判断有序范围内有没有,更新left或right指针,不断缩小范围
注意里面的 “==” 号
class Solution {
public:
int search(vector<int>& nums, int target) {
int l = 0, r = nums.size() -1;
while (l <= r)
{
int mid = (l + r) >> 1;
if (target == nums[mid]) return mid; //这儿已经判断了等号了,下面没有等号
if ( nums[mid]>= nums[l]) //在左边,左边有序
{
if (target >= nums[l] && target < nums[mid])//在有序的半段里用首尾两个数来判断目标值是否在这一区域内
r = mid-1;//说明在mid~right内,更新left位置
else
l = mid+1;
}
else if(nums[mid]<nums[l])//在右边
{
if (target > nums[mid] && target <= nums[r])
l = mid +1;
else
r = mid -1;
}
}
return -1;
}
};
❀❀❀
(6)81. 搜索旋转排序数组 II(存在重复数字)
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如,数组 [0,0,1,2,2,5,6] 可能变为 [2,5,6,0,0,1,2] )。
编写一个函数来判断给定的目标值是否存在于数组中。若存在返回 true,否则返回 false。
示例 1:
输入: nums = [2,5,6,0,0,1,2], target = 0
输出: true
示例 2:
输入: nums = [2,5,6,0,0,1,2], target = 3
输出: false
思路:二分查找,与33的区别只加了2行
//处理重复数字
while(l<r&&nums[l]==nums[l+1]) ++l;
while(l<r&&nums[r]==nums[r-1]) --r;
每次二分,左半部分和右半部分至少有一边是有序的,以此为条件可以分成两种情况:
1、左半边是有序的
(1) target落在左半边
(2) otherwise
2、右半边是有序的
(1) target落在右半边
(2) otherwise
综上所述,一共两种可能性,这两种情况各自又有两种可能性,代码如下:
class Solution {
public:
bool search(vector<int>& nums, int target) {
int l = 0, r = nums.size() -1;
while (l <= r)
{
//处理重复数字
while(l<r&&nums[l]==nums[l+1]) ++l;
while(l<r&&nums[r]==nums[r-1]) --r;
int mid = (l + r) >> 1;
if (target == nums[mid]) return true; //这儿已经判断了等号了,下面没有等号
if ( nums[mid]>= nums[l]) //在左边,左边有序
{
if (target >= nums[l] && target < nums[mid])//在有序的半段里用首尾两个数来判断目标值是否在这一区域内
r = mid-1;//说明在mid~right内,更新left位置
else
l = mid+1;
}
else if(nums[mid]<nums[l])//在右边,右半部分有序
{
if (target > nums[mid] && target <= nums[r])
l = mid +1;
else
r = mid -1;
}
}
return false;
}
};
❀❀❀
(7)88. 合并两个有序数组
法1:从后往前扫描,依次复制(未开辟额外空间,效率更优)
给定两个有序整数数组 nums1 和 nums2,将 nums2 合并到 nums1 中,使得 num1 成为一个有序数组。
说明:
初始化 nums1 和 nums2 的元素数量分别为 m 和 n。
你可以假设 nums1 有足够的空间(空间大小大于或等于 m + n)来保存 nums2 中的元素。
示例:
输入:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6], n = 3
输出: [1,2,2,3,5,6]
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int i=m-1, j=n-1, k=nums1.size()-1;//从后往前扫描, i,j分别指向有序数组末尾,k指向nums1空间的末尾
while(i>=0 && j>=0){
nums1[k--]=nums1[i]>nums2[j] ? nums1[i--]:nums2[j--];
}
while(j>=0){ //将nums2剩余元素复制过去
nums1[k--]=nums2[j--];
}
}
};
法2:用sort,不推荐
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int i=nums1.size()-1;
for(int j=0; j<nums2.size(); ){
nums1[i--]=nums2[j++];
}
sort(nums1.begin(),nums1.end());
}
};
❀❀❀
(8)162. 寻找峰值
峰值元素是指其值大于左右相邻值的元素。
给定一个输入数组 nums,其中 nums[i] ≠ nums[i+1],找到峰值元素并返回其索引。
数组可能包含多个峰值,在这种情况下,返回任何一个峰值所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞。
示例 1:
输入: nums = [1,2,3,1]
输出: 2
解释: 3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入: nums = [1,2,1,3,5,6,4]
输出: 1 或 5
解释: 你的函数可以返回索引 1,其峰值元素为 2;
或者返回索引 5, 其峰值元素为 6。
说明:
你的解法应该是 O(logN) 时间复杂度的。
法1:暴力,最大值肯定是极大值
class Solution {
public:
int findPeakElement(vector<int>& nums) {
int Max_index=0;
for(int i=0; i<nums.size(); i++){
if(nums[i]>nums[Max_index]) Max_index=i;
}
return Max_index;
}
};
法2: 二分查找
当两个“指针”相遇时,就可以满足极大值条件(两个指针按二分跨度走,故效率较高)
举例:
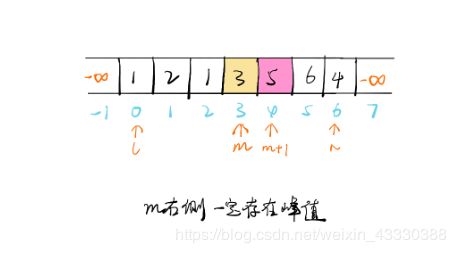
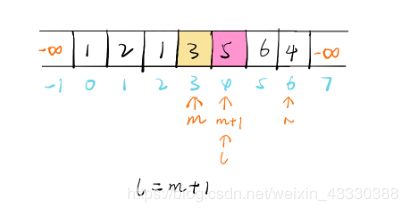
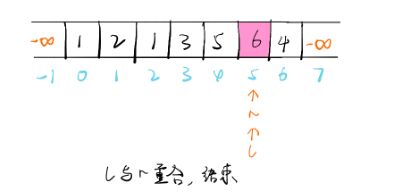
class Solution {
public:
int findPeakElement(vector<int>& nums) {
int left = 0, right = nums.size() - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] > nums[mid + 1]) {// 左边高,说明左边有峰值,可能mid就是
right = mid; // mid在下一次查找中还要考虑在内
} else {
left = mid + 1;// 右边高,说明在mid右边有峰值,所以mid一定不是
}
}
return left;
}
};
❀❀❀
(9)278. 第一个错误的版本
你是产品经理,目前正在带领一个团队开发新的产品。不幸的是,你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, ..., n],你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。
示例:
给定 n = 5,并且 version = 4 是第一个错误的版本。
调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true
所以,4 是第一个错误的版本。
思路:二分查找
二分,注意边界。
不能写 int mid = (lo + hi) / 2; 要写 int mid = lo + (hi - lo) / 2;
这个题目,返回 lo 或者 hi 都行,因为终止条件是 lo == hi.
这是二分里比较难的题目了吧,找的是分割点,不是某个值。
[********########] 就像这样的有序数组,找第一个 # 号。
二分搜索的演化版本,查找某个值,返回其索引,如果找不到,返回其本来应该所在的位置(比如上面 # 号的位置)。遇到这种二分搜索,就拿这个 bad version 来套就行了。
代码:
// Forward declaration of isBadVersion API.
bool isBadVersion(int version);
class Solution {
public:
//序列可看成(0,0,0,0,1,1,1,1,1,1,1,1,1,1)找第一个为1的数(可用lower_bound函数)
int firstBadVersion(int n) {
int lo = 1;
int hi = n; //相当于闭区间
while(lo < hi) {
int mid = lo + (hi - lo) / 2;
if (isBadVersion(mid)) {
hi = mid;
} else {
lo = mid + 1;
}
}
return hi;
}
};
//一般的二分查找
while(left <= right) //注意这里为<=,因为要计算一次mid再返回
{
mid = left + (right - left)/2; //防止(left+right)/2造成溢出风险
if(a[mid]<key)
{
left = mid + 1;
}
else if(a[mid]>key)
{
right = mid -1;
}
else
{
return mid;
}
}
❀❀❀
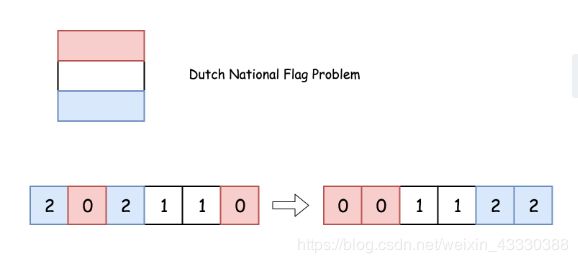
(10)75. 颜色分类(荷兰国旗)
给定一个包含红色、白色和蓝色,一共 n 个元素的数组,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
此题中,我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
注意:
不能使用代码库中的排序函数来解决这道题。
示例:
输入: [2,0,2,1,1,0]
输出: [0,0,1,1,2,2]
思路:三指针
class Solution {
public:
void sortColors(vector<int>& nums) {
// curr 是当前考虑元素的下标
int p0 = 0, curr = 0;
int p2 = nums.size() - 1;
while (curr <= p2) {
if (nums[curr] == 0) {
swap(nums[curr++], nums[p0++]);
}
else if (nums[curr] == 2) {
swap(nums[curr], nums[p2--]);//因为P2交换过来的数字还没经过确认,所以curr不++
}
else curr++;//如果不是0也不是2就++
}
}
};
超时!×
class Solution {
public:
void sortColors(vector<int>& nums) {
int left=0,right=nums.size()-1;//双指针,left从左边扫描,right从右边扫描
for(int i= 0;i<=right;){//扫描到right即可
if(nums[i] == 0) swap(nums[i++],nums[left++]); //将0换到左边
else if(nums[i] == 2) swap(nums[i++],nums[right--]);
}
}
};
❀❀❀
(11)347. 前 K 个高频元素
优先队列模拟堆
此题比较难,哈希和堆结合!pair
给定一个非空的整数数组,返回其中出现频率前 k 高的元素。
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:
输入: nums = [1], k = 1
输出: [1]
class Solution {
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int,int> mp;//出现频次计数器map
priority_queue<pair<int,int> > pq; //书p380
for(auto n:nums) mp[n]++;//按<数字,频次>
for(auto m:mp) pq.push(make_pair(m.second,m.first));//按<频次,数字> 组织,构建一个大顶堆。频数大的在前面!(个人理解)
vector<int> res;
for(int i=0;i<k;i++) {//输出前k个最大值
res.push_back(pq.top().second);
pq.pop();
}
return res;
}
};
//时间分析:
//构建map耗时O(n),构建大顶堆O(nlogn),输出前k个数O(klogn),时间复杂度O(nlogn)
❀❀❀
(12)56. 合并区间
给出一个区间的集合,请合并所有重叠的区间。
示例 1:
输入: [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入: [[1,4],[4,5]]
输出: [[1,5]]
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
二维数组排序,按第一个元素排
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
if(intervals.empty())
return {};
sort(intervals.begin(),intervals.end()); //二维数组排序,按第一个变量排序
vector<vector<int>> res; //保存结果
res.push_back(intervals[0]); //先把第一个区间送入
for(int i=1;i<intervals.size();++i){ //从第二个区间开始到结束
if(res.back()[1]>=intervals[i][0]){//res.back()返回的是最后一个数组,这时它已经是一个一维数组了,res.back()[1]返回最后一个数组的第二个元素
res.back()[1]=max(res.back()[1],intervals[i][1]);
}
else{
res.push_back(intervals[i]);
}
}
return res;
}
};