2019牛客暑期多校训练营（第一场）----I-Points Division

首先发出题目链接：
链接：https://ac.nowcoder.com/acm/contest/881/I
来源：牛客网
涉及：线段树，dp

点击这里回到2019牛客暑期多校训练营解题—目录贴

---

题目如下：


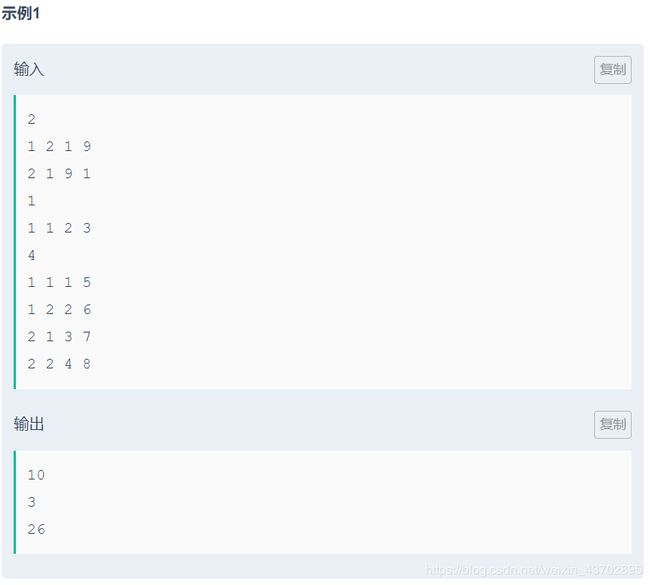
前面说一下，这个题用了线段树维护区间最大值的板子，然后我就用我自己写的线段树维护区间和的板子改了一下，后面出现了各种bug，最后把懒标记处理了一下才过的，所以还是自己乖乖重新写一遍线段树维护区间最大值的板子吧。很蓝瘦。

---

题目意思改一下：题目说不合法的分割方式是集合A内的点在集合B内点的右下方（包括正右方和正下方），也就是说合法的方式即为集合A的点要么在集合B内点的左方，要么在集合B内点的上方。

也就是说，所有的点在一个平面内，我们用一个不向下减的折线把点分成两个区间就OK了。

折线以上的部分属于A集合，折线包括折线以下的部分属于B集合

如下图分割方法属于一种合理方式

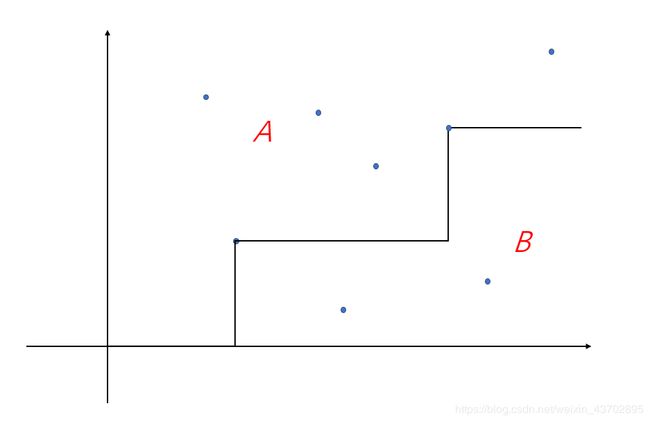
每个点都有两个值$a_i$和$b_i$可当为此点的权值。

A集合点的权值我们取$a_i$值，B集合点的权值我们取$b_i$值。

由于将平面上的点划分成A,B两个集合有很多种情况，所以求一种划分情况，使得所有点权值的最大值。

请注意，刚开始就存在一条已知的折线，即x轴，此时所有的点都在A集合内。

---

首先解释一下折线的权值，也就是说一条折线可以把目前已经考虑的点分成两部分（没有考虑到的点先不管），已经考虑的点的权值之和，就是这条折线的权值（注意选取$a_i$还是$b_1$为点权值），比如说：

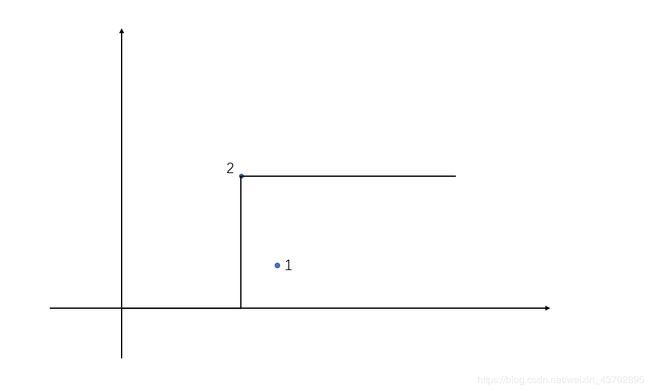
那么图中折线的权值为点1的权值+点2的权值（$b_1+b_2$）。
如果再向图中加入另一个点3且在折线上方，那么此折线的权限就要更新为点1的权值+点2的权值+点3的权值（$b_1+b_2+a_3$）

初始折线x轴，当没有考虑任何点时，这条折线的权值为0。

---

一条折线可以由比它低的折线中，权值最大的那条折线得来，比如说图中有三个点

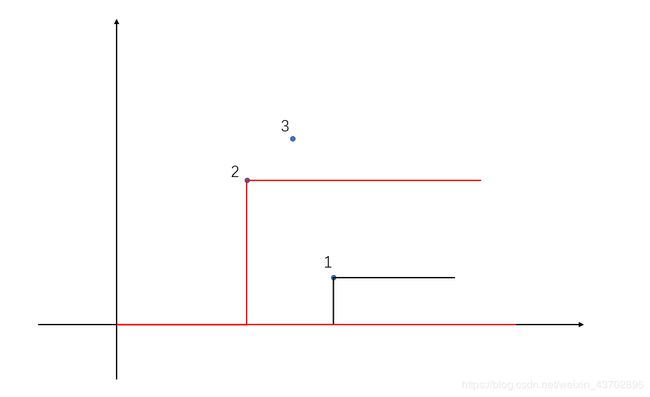
当我们已经考虑了1号点和2号点，现在考虑3号点，那么经过3号点的折线，可以由进过2号点的折线或者x轴折线得来（图中两条红色折线）

但是注意不可能由经过1号点的折线得来，虽然1号点的折线比3号点低，但是1号点的横坐标比三号点大
（为了防止这种情况，可以首先对所有点按照横坐标从小到大的循序先排序，排序后再依次考虑点就不会发生这种情况）

此时经过2号点的折线和x轴折线都有了权值，假设此时进过2号点的折线权值比较大，那么经过3号点的折线就由经过2号点的折线得来，如图所示

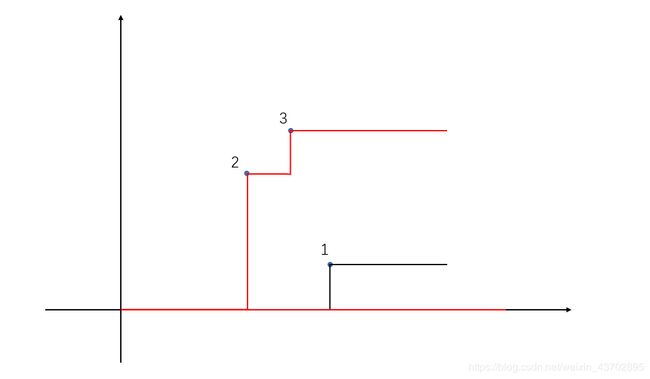
设最后经过$i$号点折线的权值为$f(i)$，那么此时$f(3)=f(3)+b_3$，3号点经过折线，所以3号点的权值为$b_3$，同理还要更新其他折线的权值

比$f(3)$折线要低的折线权值要加上$a_3$，因为此时3号点相对于在这些折线的上方。
比$f(3)$折线要高的折线权值要加上$b_3$，因为此时3号点相对于在这些折线的下方。

---

所以先将所有点的y值离散化，然后对x值从大到小排序，然后开始考虑每一个点
离散代码（我感觉我的离散方法很垃圾）

for(i=1;i<=n;i++)	scanf("%lld%lld%lld%lld",&po[i].x,&po[i].y,&po[i].a,&po[i].b); //输入点
sort(po+1,po+n+1,comp1);//对y值从小到大排序
for(i=1;i<=n;i++){//place存离散后的y值
    if(i==1)    po[i].place=1;//y值最小点，离散后为1
    else if(po[i].y==po[i-1].y) po[i].place=po[i-1].place;//y值相同，离散后的值也相同
    else    po[i].place=po[i-1].place+1;//因为从小到大排序，所以y值不同，离散后就加1
}
ll flag=po[n].place;//y值离散后的最大值
build(0,flag+1,1);//创建线段树
sort(po+1,po+n+1,comp2);//按照x值对所有点排序

排序后，每考虑新的一个点i，此点$y$值离散化后的值为$y_i$，首先求出经过$i$点折线的最大权值（注意一开始就有一条折线，x轴）
$$f(y_i)=\underset{y_j\le y_i}{\max }f(y_j)+b_{i}1$$
然后更新其他折线
$$f(y_j)=\{\begin{array}{ll}f(y_j)+a_i& y_i>y_i\\ f(y_j)+b_i& y_i\le y_i\end{array}2$$

很明显以上操作包括求区间最大值（操作1）以及为一片区间赋值（操作2），需要用线段树动态维护区间最值，网上有线段树维护区间最值的板子，我自己的板子我感觉非常垃圾。

基本代码

for(i=1;i<=n;i++){
    point q=po[i];//考虑当前点（结构体类型）
    add(q.place,ask(0,q.place,1)+q.b,1);//更新经过此点的折线的最大权值，q.place是离散后的y值
    change(0,q.place-1,q.a,1);//更新比此折线要低的折线的权值
    change(q.place+1,flag+1,q.b,1);//更新比次折线要高的折线的权值
}

这就是利用线段树加dp

---

忘记说了，为啥创建线段树要从0到flag+1

build(0,flag+1,1);

第一是为了下文访问$q.place-1$和$q.place+1$时越界（change函数里面访问了）

第二是零开始是初始化x轴这条折线（x轴折线一开始就有），如果一开始不考虑x轴这条折线是会报错的，因为有的折线可能直接由x轴这条折线dp得来，给你一组数据你就知道了

3
7831 5883 18334 7062
19558 16417 1551 1860
2595 994 5414 846

本人调bug用的测试数据

15
16966 32485 13587 20526
29080 23068 18650 26437
12638 5820 10030 30162
29365 20219 12305 9347
18281 30733 16501 21517
23408 1431 4434 718
10167 24934 3319 13745
16930 2913 3742 26707
28366 30140 16450 18532
22169 29039 2741 16463
1764 16103 19437 5405
7831 5883 18334 7062
19558 16417 1551 1860
2595 994 5414 846
4628 6283 24516 19501

还有一个问题：为啥在comp2函数中还要对y进行从大到小排序

bool comp2(point pa,point pb){
    if(pa.x!=pb.x)  return pa.x<pb.x;
    return pa.y>pb.y;
}

针对这个问题，我们选取三个点

3
2 1 1 5
2 2 10 1
2 3 3 3

如果从大到小排序后，然后遍历每个点，是这样的情况（正常情况）：

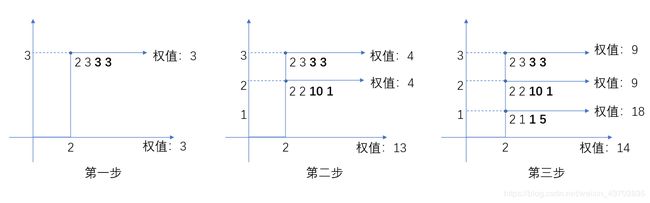
如果从小到大排序，则是下面情况，红色权值有错误

---

代码如下：

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
const int maxn=1e5+4;
struct point{
//x,y,a,b是题目所给变量
    ll x;
    ll y;
    ll a;
    ll b;
    ll place;//place是y值离散后的值
};
point po[maxn+5];//点数组
struct p{//线段树节点数组
    int l;
    int r;
    ll lazy;
    ll sum;
};
p tree[4*maxn+2];
void push(int k){ //推懒标记
	if(2*k+1<=4*maxn){
		tree[2*k].lazy+=tree[k].lazy;
    	tree[2*k+1].lazy+=tree[k].lazy;
    	tree[2*k].sum+=tree[k].lazy;
    	tree[2*k+1].sum+=tree[k].lazy;
    	tree[k].lazy=0;
	}
    return;
}
void build(int l,int r,int k){//创建线段树，l~r是范围，k表示当前节点的编号
    tree[k].l=l;
    tree[k].r=r;
    tree[k].lazy=0;
    tree[k].sum=0;
    if(l==r)    return;
    int pos=(l+r)/2;
    build(l,pos,2*k);
    build(pos+1,r,2*k+1);
    return;
}
void add(int x,ll z,int k){//单点修改，x是单点位置，z是修改的值，k表示当前节点的编号
	if(tree[k].lazy)    push(k);
    if(tree[k].l==tree[k].r)
        return (void)(tree[k].sum=z);
    int pos=(tree[k].l+tree[k].r)/2;
    if(x<=pos)    add(x,z,2*k);
    else    add(x,z,2*k+1);
    tree[k].sum=max(tree[2*k].sum,tree[2*k+1].sum);
    return;
}
ll ask(int l,int r,int k){//询问区间最大值，l~r是区间，k表示当前节点的编号
	if(tree[k].lazy)    push(k);
    if(tree[k].l>=l && tree[k].r<=r)    return tree[k].sum;
    int pos=(tree[k].l+tree[k].r)/2;
    
    return max((l<=pos?ask(l,r,2*k):0),(r>pos?ask(l,r,2*k+1):0));
}
void change(int l,int r,ll x,int k){//区间修改，l~r是区间，x是修改值，k表示当前节点的编号
	if(tree[k].lazy)    push(k);
    if(tree[k].l>=l && tree[k].r<=r){
        tree[k].sum+=x;
        tree[k].lazy+=x;
        return;
    }
    int pos=(tree[k].r+tree[k].l)/2;
    if(l<=pos)    change(l,r,x,2*k);
    if(r>pos)    change(l,r,x,2*k+1);
    tree[k].sum=max(tree[2*k].sum,tree[2*k+1].sum);
    return;
}
bool comp1(point pa,point pb){
    return pa.y<pb.y;
}
bool comp2(point pa,point pb){
    if(pa.x!=pb.x)  return pa.x<pb.x;
    return pa.y>pb.y;
}
int main(){
    int n;
    int i;
    while(~scanf("%d",&n)){
        for(i=1;i<=n;i++)	scanf("%lld%lld%lld%lld",&po[i].x,&po[i].y,&po[i].a,&po[i].b); //输入点
        sort(po+1,po+n+1,comp1);//对y值从小到大排序
        for(i=1;i<=n;i++){//place存离散后的y值
            if(i==1)    po[i].place=1;//y值最小点，离散后为1
            else if(po[i].y==po[i-1].y) po[i].place=po[i-1].place;//y值相同，离散后的值也相同
            else    po[i].place=po[i-1].place+1;//因为从小到大排序，所以y值不同，离散后就加1
        }
        ll flag=po[n].place;//y值离散后的最大值
        build(0,flag+1,1);//创建线段树
        sort(po+1,po+n+1,comp2);//按照x值对所有点排序
        for(i=1;i<=n;i++){
            point q=po[i];//考虑当前点（结构体类型）
            add(q.place,ask(0,q.place,1)+q.b,1);//更新经过此点的折线的最大权值，q.place是离散后的y值
            change(0,q.place-1,q.a,1);//更新比此折线要低的折线的权值
            change(q.place+1,flag+1,q.b,1);//更新比次折线要高的折线的权值
        }
        printf("%lld\n",tree[1].sum);//输出全部最大值
    }  
    return 0;
}