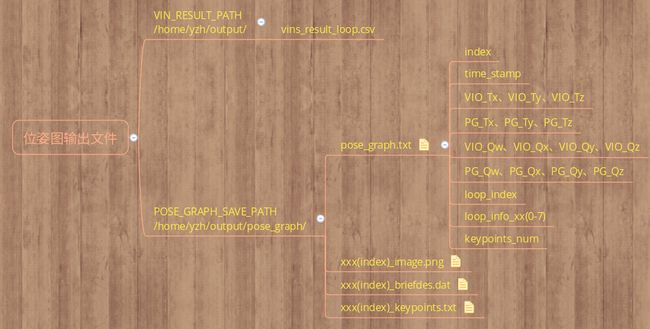
vins位姿图优化
我们 的滑动窗口和边缘化方案限制了计算的复杂性，但也给系统带来了累积漂移。更确切地说，漂移发生在全局三维位置(x,y,z)和围绕重力方向的旋转(yaw)。为了消除漂移，提出了一种与单目VIO无缝集成的紧耦合重定位模块。
论文内容
1. 回环检测
利用DBoW2词袋模型进行回环检测，除了用于单目VIO的角点特征外，另外500个fast角点被检测出来并有brief描述子描述。额外的角点特征用于在回环检测中实现更好的召回率。DBoW2在时间和空间一致性检验后返回回环候选帧。（好像没有）
2. 特征恢复
检测到回环帧后，通过检索特征对应关系建立局部滑动窗口与回环候选帧之间的连接。通过brief描述子匹配找到对应关系(用的暴力匹配，可以考虑用DBoW2中的数据库中的顺序索引，加速匹配）。直接匹配描述子可能会造成大量异常值，为此，论文使用两步进行集合异常值剔除(代码中只用了pnp)：
1、2D-2D：RANSAC[31]的基本矩阵检验。我们利用当前图像中检索到的特征的二维观测和回环候选图像进行基本矩阵检验。
2、3D-2D：RANSAC的PNP检验。基于特征在局部滑动窗口中已知的三维位置，以及回环候选图像中的二维观测，进行PNP检验。
当内点超过一定阈值时，我们将该候选帧视为正确的循环检测并执行重定位。
3. 快速重定位
检测出回环帧之后，返回回环帧的信息给vins_estimator节点，在窗口优化后，得到loop_info信息
此时窗口优化的代价函数变为：
min x { ∥ r p − H p X ∥ 2 + ∑ k ∈ B ∥ r B ( z ^ b k + 1 ′ b k , X ) ∥ P k + 1 b k + 1 + ∑ ( l , j ) ∈ C ∥ r C ( z ^ l c j , X ) ∥ P l C j 2 + ∑ ( l , v ) ∈ L ∥ r C ( z ^ l v , X , q ^ v w , p ^ v w ) ∥ P l 2 c v } \min _{x}\left\{\left\|r_{p}-H_{p} X\right\|^{2}+\sum_{k \in B}\left\|r_{B}\left(\hat{z}_{b_{k+1}^{\prime}}^{b_{k}}, X\right)\right\|_{P_{k+1}^{b_{k+1}}}+\sum_{(l, j) \in C}\left\|r_{C}\left(\hat{z}_{l}^{c_{j}}, X\right)\right\|_{P_{l}^{C_{j}}}^{2}+\right. \left.\sum_{(l, v) \in \mathcal{L}}\left\|r_{C}\left(\hat{z}_{l}^{v}, X, \hat{q}_{v}^{w}, \hat{p}_{v}^{w}\right)\right\|_{P_{l}}^{2} c_{v}\right\} xmin⎩⎨⎧∥rp−HpX∥2+k∈B∑∥∥∥rB(z^bk+1′bk,X)∥∥∥Pk+1bk+1+(l,j)∈C∑∥∥rC(z^lcj,X)∥∥PlCj2+(l,v)∈L∑∥rC(z^lv,X,q^vw,p^vw)∥Pl2cv⎭⎬⎫
4. 四自由度全局优化
当检测到了回环帧后才进行优化
通过最小化以下代价函数，对顺序边和回环边的整个图进行优化：
min p , ψ { ∑ ( i , j ) ∈ S ∥ r i , j ∥ 2 + ∑ ( i , j ) ∈ L h ( ∥ r i , j ∥ 2 ) } \min _{p, \psi}\left\{\sum_{(i, j) \in \mathcal{S}}\left\|r_{i, j}\right\|^{2}+\sum_{(i, j) \in \mathcal{L}} h\left(\left\|r_{i, j}\right\|^{2}\right)\right\} p,ψmin⎩⎨⎧(i,j)∈S∑∥ri,j∥2+(i,j)∈L∑h(∥ri,j∥2)⎭⎬⎫
其中，我们将帧i和j之间边的残差定义为：
r i , j ( p i w , ψ i , p j w , ψ j ) = [ R ( ϕ ^ i , θ ^ i , ψ i ) − 1 ( p j w − p i w ) − p ^ i j i ψ j − ψ i − ψ ^ i j ] r_{i, j}\left(p_{i}^{w}, \psi_{i}, p_{j}^{w}, \psi_{j}\right)=\left[\begin{array}{c}{R\left(\hat{\phi}_{i}, \hat{\theta}_{i}, \psi_{i}\right)^{-1}\left(p_{j}^{w}-p_{i}^{w}\right)-\hat{p}_{i j}^{i}} \\ {\psi_{j}-\psi_{i}-\hat{\psi}_{i j}}\end{array}\right] ri,j(piw,ψi,pjw,ψj)=[R(ϕ^i,θ^i,ψi)−1(pjw−piw)−p^ijiψj−ψi−ψ^ij]
其中S是所有序列边的集合，L是回环边的集合。尽管紧耦合的重定位已经有助于消除错误的回环，但我们添加了另一个Huber范数 ρ(·)，以进一步减少任何可能的错误回环的影响。相反，不对顺序边使用任何鲁棒范数，因为这些边是从VIO中提取出来的，VIO已经包含了足够多的外点排除机制。
序列边的集合包括：从最早回环帧到当前帧中的每一帧，它和之前最近的最多４帧产生的约束边
优化的变量初值为：Ｔ_w2_index，优化后为：T_w1_index，最终可以得到drift漂移位姿
5. 位姿图管理
随着行程距离的增加，位姿图的大小可能会无限增长，从而限制了长时间系统的实时性。为此，我们实行了一个下采样过程，将位姿图数据库保持在有限的大小。所有具有回环约束的关键帧都将被保留，而其他与相邻帧过近或方向非常相似的关键帧可能会被删除。关键帧被移除的概率和其相邻帧的空间密度成正比。(这一点在代码中没有体现)
重定位的两种方案
1. 快速重定位(fast_relocalization)
通过回环检测得到回环帧，将回环帧信息发布给vins_estimator节点在窗口中进行局部优化，得到了loop_info（T_i_j）后返回给位姿图节点，然后得到T_w1_j，结合已知的T_w2_j，得到T_w1_w2（shift_t）;
2. 全局优化重定位
通过pnp得到loop_info(T_i_j)，作为残差信息放在ceres优化中，从最早的回环帧到当前帧均为优化变量，分别添加序列约束块和回环约束块 ，序列约束选取离它最近的前4帧，回环约束就是当前帧跟回环帧，进行全局优化后的位姿为T_w1_index，结合已知的T_w2_index可以得到T_w1_w2(shift_t)
- 可以看出，重定位就是想计算出世界坐标系和vio坐标的漂移位姿（shift_t），由于快速重定位是在窗口局部优化中得到的，计算快，输出响应快，但精度较低；而全局优化重定位可以得到高精度的位姿估计。
代码解读
- ThirdParty文件夹：视觉词袋相关的第三方库
- utility文件夹：
- CameraPoseVIsualization：相机可视化化类，用来显示相机位姿和序列边、回环边的
- tic_toc：时间统计类
- utility：矩阵转换等一些工具类
- parmaters：外部全局参数的头文件
- keyframe：关键帧类
- pose_graph：位姿图类
- pose_grap_node：位姿图节点主函数
1. keframe类
- 关键帧作为位姿图位姿图中重要的数据类型，类代码如下：
- 代码思维导图：
2. pose_graph类
- 位姿图类主要负责对检测到的回环帧进行全局位姿优化，在添加新创建的关键帧后，需要进行回环检测(并优化)，并发布path话题
- 代码思维导图：
3. 节点主函数
- 主要是创建pose_graph实例，接收话题，发布话题，其中开辟了多个线程执行多任务
- 代码思维导图：
- 多线程：
- 输出文件：
- 辅助文件：
pose_graph节点主要流程
- 主线程接受话题消息，并创建pose_graph实例(同时开辟全局优化线程)，如果需要则预加载已有位姿图文件到psoe_graph实例中
- 子线程process根据接收的消息，创建新的keyframe实例，添加进入pose_graph实例中
- pose_graph对添加的新keyframe进行回环检测，如果发现回环则进行全局优化，得到drift漂移量
- 根据drift偏移量，更新全局位姿，发布path路径话题信息
部分话题输出（rviz）
- 回环帧的匹配的调试图像
- 相机可视化
- Odometry输出
- pose_graph_path路径输出
文件输出
