矩形牛棚——浅谈C++单调队列和单调栈
矩形牛棚 BZOJ 1114
目录
前言
正文
解析
单调栈
前言
厉害的是,这道题在LGOJ上面又没有。
这道题也算花了我比较多的时间哈,不过其实只是利用单调栈求解一个最大长方形。
正文
题目描述
到底是个资本家,Farmer John想通过买更多的奶牛来扩大它的生意。它需要给奶牛建造一个新的牛棚。 FJ买了一个矩形的R(1 <= R <= 3000)行C(1 <= C <= 3000)列的牧场。不幸的是,他发现某些1 x 1的区域被损坏了,所以它不可能在把整个牧场建造成牛棚了。
FJ数了一下,发现有P(1 <= p <= 30000)个1 x 1的损坏区域并且请你帮助他找到不包含损坏区域的面积最大的牛棚。 * (对同一个损坏区域可能有多次描述——aLeN.PN注)
输入
第1行: 三个空格隔开的整数 R, C, and P.
第2..P+1行: 每行包含两个空格隔开的整数, r和c, 给出一个损坏区域的行号和列号.
输出
第1行: 牛棚的最大可能面积
样例输入
3 4 2
1 3
2 1样例输出
6
解析
可以看到哈,这道题呢很简单,(前面也提到过)就是在一个r行c列的区域里面找到一个最大的没有被损坏的长方形。
这么一看起来,似乎就跟最大正方形有点渊源了。戳
因为毕竟是求最大长方形,所以我就不再多说正方形的事了。
这个呢,跟最大矩形面积就差不多了。
在这里将引入一个新内容——单调栈!
单调栈
单调栈,顾名思义,就是在栈中通过一系列的出栈、入栈等操作,使栈里的元素维持单调性。
在这里,我们可以维持单调递增的序列,通过维护单调栈的单调性来求解。
例如:
有一个begin数组和end数组,分别存的每个数什么时候入栈,什么时候出栈。
因为这里的栈是维持单调递增的,所以该元素如果比栈首小的话,就把栈首推出,一直到栈首小于该元素为止,然后将该元素插入到栈首的上方,成为新的栈首。
反之亦然。
这里有个问题:什么时候才是开始,什么时候是结束呢?
可以看到,在上方的维护单调的步骤中,他插入到了第一个比他小的元素后面,所以就可以把那个元素的下标加1赋给插入元素的开始;而什么时候他被踢出栈的时候,就可以把他的结尾赋为把他踢出去的元素减1。
当然,有人或许会问了,为什么要这样搞呢?
且看:
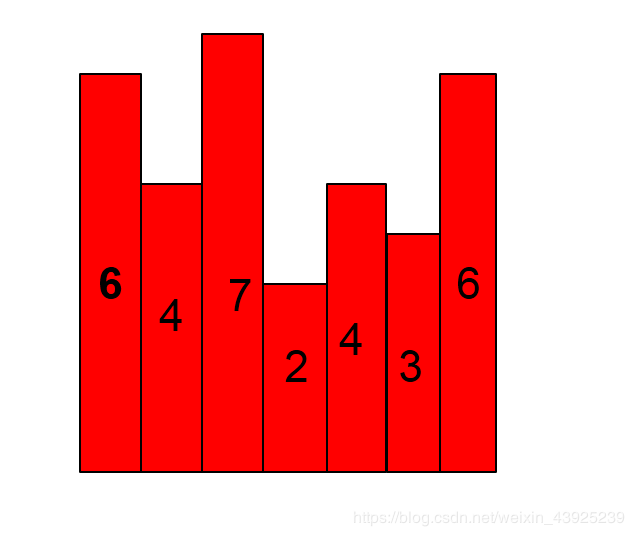
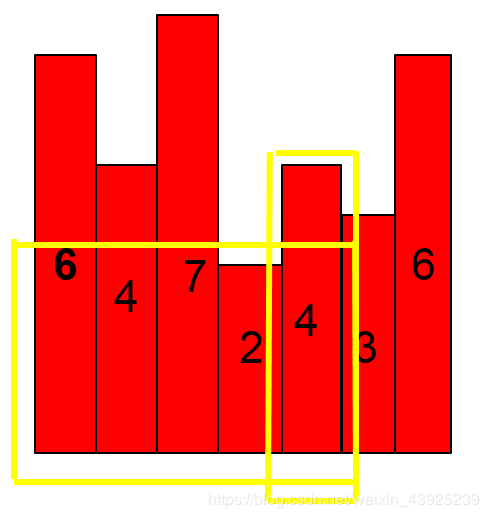
假设这是一些大楼,然后要在这些大楼中放置一块广告牌(矩形),使该广告牌的面积最大。可是有些约束:广告牌不能“随风飘扬”,即它背后必须有大楼。可以看出,就是求一个最大的长方形。
那么我们来 枚举 假想以每一栋大楼的高度为广告牌的高度,那么问题就转变为了求以每一栋大楼为高度的最长宽度,也就是以这座大楼为起点,分别向左和向右开始的第一栋比它还矮的大楼的位置之差。
可是有一个很现实的问题,那就是时间复杂度。只要n的取值一大起来,那么铁定超时。
可是如果用单调栈的话,那么每个元素只会进一次,出一次,维护一个单调栈的时间复杂度只是O(2 * n),也就是O(n)的复杂度!
接着,我们来走一遍吧。
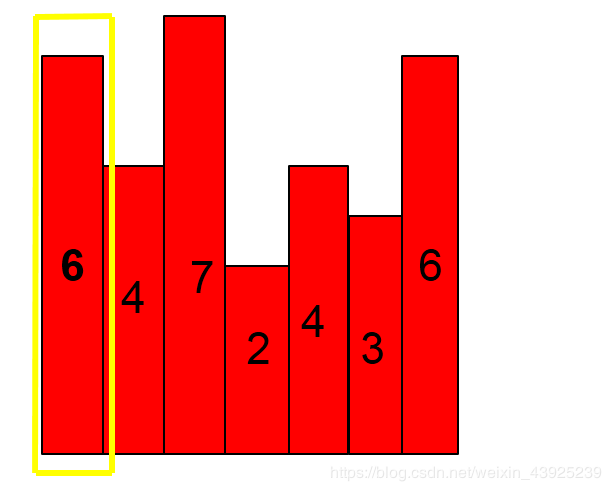
首先,枚举第1个大楼的高度为高度。
他先进栈,开始位置为1。
第2个
他的高度小于了栈顶的高度,把栈顶元素踢出,然后因为栈空了,所以他就是栈顶元素,开始位置为1。
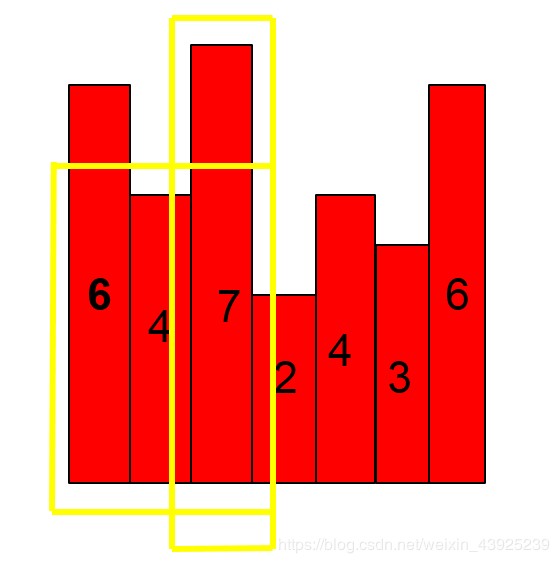
第3个
它的高度大于了栈顶元素,直接加到栈顶,第二个元素的右边又加1了。
他的开始为3
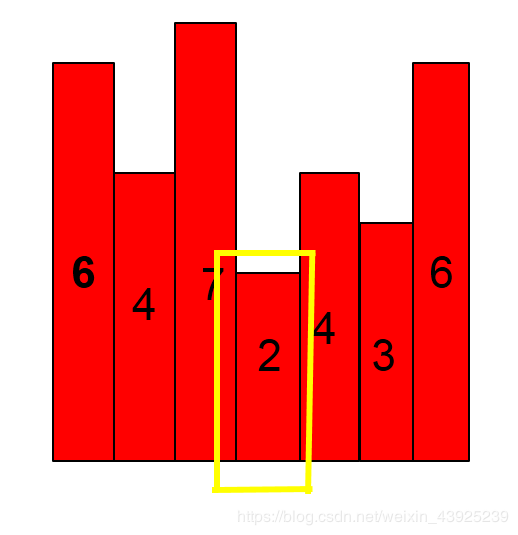
第4个
它的高度小于了栈顶元素,于是一个个都被踢了出去,然后结尾也变成了这个元素下标减1。
因为栈已经空了,所以他变为栈顶元素,开始为1。
第5个
它大于了栈顶元素,直接加到栈顶,而第四个的结尾加1。
他的开始元素为5。
……
一直到最后,可以看到,最大的面积就是以第四个元素高度为高度的矩形面积,他把所有的都囊括了,也就是14。
参考代码:
#include
#include
#define MAXN 100000
#define max(a, b) a > b ? a : b
using namespace std;
struct node{
int h, s, e;
}a[MAXN + 5];
int n, ans;
stack S;
int main (){
scanf ("%d", &n);
for (int i = 1; i <= n; i++){
scanf ("%d", &a[i].h);
}
S.push (0);
for (int i = 1; i <= n + 1; i++){
while (!S.empty ()){
int x = S.top ();
S.pop ();
if (a[i].h <= a[x].h){
a[x].e = i - 1;
ans = max (ans, (a[x].e - a[x].s + 1) * a[x].h);
continue;
}
else{
a[i].s = x + 1;
S.push (x);
S.push (i);
break;
}
}
}
printf ("%d\n", ans);
}
这里为什么要先push一个0呢?原因就是可能是第一个元素,因为栈是空的,所以进不去,以后也都进不去;也有可能是某个元素小于了所有栈里存的元素,把它们都踢出去了,自己也存不进去,所以就象征性的加一个0。
或许会有细心的大佬看到了循环要素是循环到n + 1,这个跟上面差不多,也是因为可能栈里会存有一些元素到了最后,可是并没有赋上结尾就直接退出了,所以也象征性的加一个0在结尾。
当然,这是最大矩形面积的代码哈,希望不会有些心急的人直接复制粘贴了。
前面说过,矩形牛棚跟最大矩形面积很像,那是哪里有些差别呢?答案就是会多一重枚举!
他会枚举每一层作为起点来统计最大面积。至于为什么要这样呢?是因为在牛棚中间也许会有残缺,所以不能直接单纯的用上方的代码求解,还需要一个巧妙的东西——前缀和。
参考代码:
#include
#include
const int MAXN = 3000;
#define max(a, b) a > b ? a : b
using namespace std;
int r, c, p, pre_sum[MAXN + 5][MAXN + 5];
int ans, be[MAXN + 5], en[MAXN + 5];
bool farm[MAXN + 5][MAXN + 5];
struct node{
int id, num;
node (){};
node (int ID, int NUM){
id = ID;
num = NUM;
}
};
stack S;
void read (int &x){
x = 0;
char c = getchar ();
while (c < '0' || c > '9')
c = getchar ();
while (c >= '0' && c <= '9'){
x = (x << 1) + (x << 3) + c - 48;
c = getchar ();
}
}
int main (){
read (r); read (c); read (p);
for (int i = 1; i <= p; i++){
int R, C;
read (R); read (C);
farm[R][C] = 1;
}
for (int j = 1; j <= c; j++){
for (int i = 1; i <= r; i++){
pre_sum[i][j] = farm[i][j] ? 0 : pre_sum[i - 1][j] + 1;
}
}
for (int i = r; i > 0; i--){
while (!S.empty ()){
S.pop ();
}
S.push (node (0, 0));
for (int j = 1; j <= c + 1; j++){
int x = pre_sum[i][j];
while (!S.empty ()){
node t = S.top (); S.pop ();
if (x < t.num){
en[t.id] = j - 1;
ans = max (ans, (en[t.id] - be[t.id] + 1) * t.num);
continue;
}
else{
be[j] = t.id + 1;
S.push (t);
S.push (node (j, x));
break;
}
}
}
}
printf ("%d\n", ans);
}