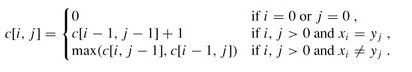腾讯面试题-回文构造

题目描述：

给定一个字符串s，你可以从中删除一些字符，使得剩下的串是一个回文串。如何删除才能使得回文串最长呢？
输出需要删除的字符个数。

输入描述:

输入数据有多组，每组包含一个字符串s，且保证:1<=s.length<=1000.

输出描述:

对于每组数据，输出一个整数，代表最少需要删除的字符个数。

输入例子:

abcda
google

输出例子:

2
2

思路分析：

首先求s的反串rs，然后对s和rs求最长公共子序列，要删除的字符个数就是LCS.

核心代码:

求最大公共子序列

public class ComSubstr {  

    public static void main(String[] arg) {  
        String a = "blog.csdn.net";  
        String b = "csdn.blogt";  
        comSubstring(a, b);  
    }  

    private static void comSubstring(String str1, String str2) {  
        char[] a = str1.toCharArray();  
        char[] b = str2.toCharArray();  
        int a_length = a.length;  
        int b_length = b.length;  
        int[][] lcs = new int[a_length + 1][b_length + 1];  
        // 初始化数组  
        for (int i = 0; i <= b_length; i++) {  
            for (int j = 0; j <= a_length; j++) {  
                lcs[j][i] = 0;  
            }  
        }  
        for (int i = 1; i <= a_length; i++) {  
            for (int j = 1; j <= b_length; j++) {  
                if (a[i - 1] == b[j - 1]) {  
                    lcs[i][j] = lcs[i - 1][j - 1] + 1;  
                }  
                if (a[i - 1] != b[j - 1]) {  
                    lcs[i][j] = lcs[i][j - 1] > lcs[i - 1][j] ? lcs[i][j - 1]  
                            : lcs[i - 1][j];  
                }  
            }  
        }  
        // 输出数组结果进行观察  
        for (int i = 0; i <= a_length; i++) {  
            for (int j = 0; j <= b_length; j++) {  
                System.out.print(lcs[i][j]+",");  
            }  
            System.out.println("");  
        }  
        // 由数组构造最小公共字符串  
        int max_length = lcs[a_length][b_length];  
        char[] comStr = new char[max_length];  
        int i =a_length, j =b_length;  
        while(max_length>0){  
            if(lcs[i][j]!=lcs[i-1][j-1]){  
                if(lcs[i-1][j]==lcs[i][j-1]){//两字符相等，为公共字符  
                    comStr[max_length-1]=a[i-1];  
                    max_length--;  
                    i--;j--;  
                }else{//取两者中较长者作为A和B的最长公共子序列  
                    if(lcs[i-1][j]>lcs[i][j-1]){  
                        i--;  
                    }else{  
                        j--;  
                    }  
                }  
            }else{  
                i--;j--;  
            }  
        }  
        System.out.print("最长公共字符串是：");  
        System.out.print(comStr);  
    }  
}  

问题描述：

问题】 求两字符序列的最长公共字符子序列

注意：

并不要求子串（字符串一）的字符必须连续出现在字符串二中。

思路分析：

最优子结构和重叠子问题的性质都具有，所以要采取动态规划的算法

最长公共子序列的结构

设序列X=和Y=的一个最长公共子序列Z=，则：

1.若xm=yn，则zk=xm=yn且Zk-1是Xm-1和Yn-1的最长公共子序列；
2.若xm≠yn且zk≠xm ，则Z是Xm-1和Y的最长公共子序列；
3.若xm≠yn且zk≠yn ，则Z是X和Yn-1的最长公共子序列。

其中Xm-1=，Yn-1=，Zk-1=。

子问题的递归结构

由最长公共子序列问题的最优子结构性质可知，要找出X=和Y=的最长公共子序列，可按以下方式递归地进行：当xm=yn时，找出Xm-1和Yn-1的最长公共子序列，然后在其尾部加上xm(=yn)即可得X和Y的一个最长公共子序列。当xm≠yn时，必须解两个子问题，即找出Xm-1和Y的一个最长公共子序列及X和Yn-1的一个最长公共子序列。这两个公共子序列中较长者即为X和Y的一个最长公共子序列。

由此递归结构容易看到最长公共子序列问题具有子问题重叠性质。

例如，在计算X和Y的最长公共子序列时，可能要计算出X和Yn-1及Xm-1和Y的最长公共子序列。而这两个子问题都包含一个公共子问题，即计算Xm-1和Yn-1的最长公共子序列。

与矩阵连乘积最优计算次序问题类似，我们来建立子问题的最优值的递归关系。用c[i,j]记录序列Xi和Yj的最长公共子序列的长度。其中Xi=，Yj=。

当i=0或j=0时，空序列是Xi和Yj的最长公共子序列，故c[i,j]=0。其他情况下，由定理可建立递归关系如下：

这里写图片描述

代码：

public class ComSubstr {  
  
    public static void main(String[] arg) {  
        String a = "blog.csdn.net";  
        String b = "csdn.blogt";  
        comSubstring(a, b);  
    }  
  
    private static void comSubstring(String str1, String str2) {  
        char[] a = str1.toCharArray();  
        char[] b = str2.toCharArray();  
        int a_length = a.length;  
        int b_length = b.length;  
        int[][] lcs = new int[a_length + 1][b_length + 1];  
        // 初始化数组  
        for (int i = 0; i <= b_length; i++) {  
            for (int j = 0; j <= a_length; j++) {  
                lcs[j][i] = 0;  
            }  
        }  
        for (int i = 1; i <= a_length; i++) {  
            for (int j = 1; j <= b_length; j++) {  
                if (a[i - 1] == b[j - 1]) {  
                    lcs[i][j] = lcs[i - 1][j - 1] + 1;  
                }  
                if (a[i - 1] != b[j - 1]) {  
                    lcs[i][j] = lcs[i][j - 1] > lcs[i - 1][j] ? lcs[i][j - 1]  
                            : lcs[i - 1][j];  
                }  
            }  
        }  
        // 输出数组结果进行观察  
        for (int i = 0; i <= a_length; i++) {  
            for (int j = 0; j <= b_length; j++) {  
                System.out.print(lcs[i][j]+",");  
            }  
            System.out.println("");  
        }  
        // 由数组构造最小公共字符串  
        int max_length = lcs[a_length][b_length];  
        char[] comStr = new char[max_length];  
        int i =a_length, j =b_length;  
        while(max_length>0){  
            if(lcs[i][j]!=lcs[i-1][j-1]){  
                if(lcs[i-1][j]==lcs[i][j-1]){//两字符相等，为公共字符  
                    comStr[max_length-1]=a[i-1];  
                    max_length--;  
                    i--;j--;  
                }else{//取两者中较长者作为A和B的最长公共子序列  
                    if(lcs[i-1][j]>lcs[i][j-1]){  
                        i--;  
                    }else{  
                        j--;  
                    }  
                }  
            }else{  
                i--;j--;  
            }  
        }  
        System.out.print("最长公共字符串是：");  
        System.out.print(comStr);  
    }  
}  

输出结果：

0,0,0,0,0,0,1,2,2,2,2,  
0,0,0,0,0,0,1,2,3,3,3,  
0,0,0,0,0,0,1,2,3,4,4,  
0,0,0,0,0,1,1,2,3,4,4,  
0,1,1,1,1,1,1,2,3,4,4,  
0,1,2,2,2,2,2,2,3,4,4,  
0,1,2,3,3,3,3,3,3,4,4,  
0,1,2,3,4,4,4,4,4,4,4,  
0,1,2,3,4,5,5,5,5,5,5,  
0,1,2,3,4,5,5,5,5,5,5,  
0,1,2,3,4,5,5,5,5,5,5,  
0,1,2,3,4,5,5,5,5,5,6,  
最长公共字符串是：csdn.t  

参考：
http://www.nowcoder.com/test/question/done?tid=3778580&qid=44802
http://www.voidcn.com/blog/Do_Know/article/p-5978576.html