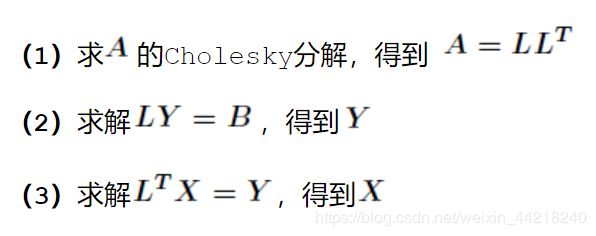深蓝学院视觉SLAM第二次习题

第二次习题来啦，线性代数和矩阵分析忘的也太快了

1.熟悉 Eigen 矩阵运算

本次习题，你需要使⽤ Eigen 库，编写程序，求解⼀个线性⽅程组。为此，你需要先了解⼀些有关线性⽅程组数值解法的原理。设线性⽅程 Ax = b，在 A 为⽅阵的前提下，请回答以下问题：

1. 在什么条件下，x 有解且唯⼀？

A满秩，行列式不为0，r(A|b)=r(A)

2. ⾼斯消元法的原理是什么？

通过用初等行变换将增广矩阵化为行阶梯阵，然后通过回带求解线性方程组的解。

3. QR 分解的原理是什么？

任意一个满秩矩阵可唯一分解成一个正规正交矩阵Q与上三角形矩阵R A= QR

4. Cholesky 分解的原理是什么？

Cholesky 分解是把一个实对称正定的矩阵表示成一个下三角矩阵L和其转置的乘积的分解。
一个实对称矩阵A正定，即存在可逆矩阵C，使得 A=C.transpose()*C

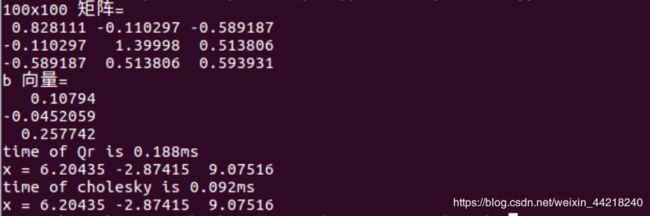
5. 编程实现 A 为 100 × 100 随机矩阵时，⽤ QR 和 Cholesky 分解求 x 的程序。你可以参考本次课⽤到的 useEigen 例程。

Cholesky 对对称正定矩阵才有效，所以需要转化一下，100x100的矩阵看不出效果，所以试了一下3x3 的矩阵

#include
#include
using namespace std;

#include
#include
using namespace Eigen;

#define MATRIX_SIZE 100

int main(int argc,char** argv)
{
  
   Matrix<double,Dynamic,Dynamic> matrix_pNN;
   matrix_pNN=MatrixXd::Random(MATRIX_SIZE,MATRIX_SIZE);
   //matrix_pNN=MatrixXd::Random(3,3);
   Matrix<double,Dynamic,1>v_Nd=MatrixXd::Random(MATRIX_SIZE,1);
   //Matrix v_Nd=MatrixXd::Random(3,1);
   Matrix<double,Dynamic,Dynamic> matrix_NN;
   matrix_NN=matrix_pNN.transpose()*matrix_pNN;
   cout<<"100x100 矩阵=\n"<<matrix_NN<<endl;
   cout<<"b 向量=\n"<<v_Nd<<endl;
   clock_t time_stt=clock();
   //QR
   Matrix<double,Dynamic,1> x=matrix_NN.colPivHouseholderQr().solve(v_Nd);
   cout<<"time of Qr is "<<1000*(clock()-time_stt)/(double)CLOCKS_PER_SEC<<"ms"<<endl;
   cout<<"x ="<<x.transpose()<<endl;
   //cholesky
   time_stt=clock();
   x=matrix_NN.ldlt().solve(v_Nd);
   cout<<"time of cholesky is "<<1000*(clock()-time_stt)/(double)CLOCKS_PER_SEC<<"ms"<<endl;
   cout<<"x ="<<x.transpose()<<endl;
   
   return 0;
}

3x3矩阵的结果可以看出QR分解需要的时间大于cholesky的时间

2.几何运算练习

设有⼩萝⼘ 1 ⼀号和⼩萝⼘⼆号位于世界坐标系中。⼩萝⼘⼀号的位姿为：q 1 = [0.55,0.3,0.2,0.2],t 1 =[0.7,1.1,0.2] T （q 的第⼀项为实部）。这⾥的 q 和 t 表达的是 T cw ，也就是世界到相机的变换关系。⼩萝⼘⼆号的位姿为 q 2 =[−0.1,0.3,−0.7,0.2],t 2 = [−0.1,0.4,0.8] T 。现在，⼩萝⼘⼀号看到某个点在⾃⾝的坐标系下，坐标为 p 1 = [0.5,−0.1,0.2] T ，求该向量在⼩萝⼘⼆号坐标系下的坐标。请编程实现此事，并提交你的程序。
提⽰：

1. 四元数在使⽤前需要归⼀化。
2. 请注意 Eigen 在使⽤四元数时的虚部和实部顺序。
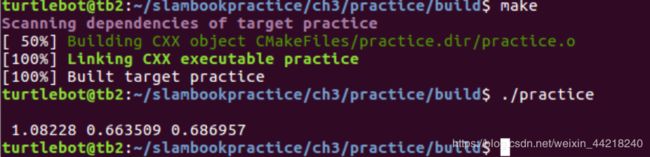
3. 参考答案为 p 2 = [1.08228,0.663509,0.686957] T 。你可以⽤它验证程序是否正确。

#include
#include
using namespace std;
#include
#include
using namespace Eigen;

int main(int argc,char **argv)
{
  Quaterniond q1(0.55,0.3,0.2,0.2),q2(-0.1,0.3,-0.7,0.2);
  Vector3d t1(0.7,1.1,0.2),t2(-0.1,0.4,0.8);
  q1.normalize();
  q2.normalize();
  Vector3d p1(0.5,-0.1,0.2);
  Isometry3d T1w(q1),T2w(q2);
  T1w.pretranslate(t1);
  T2w.pretranslate(t2);
  
  Vector3d p2=T2w*T1w.inverse()*p1;
  cout<<endl<<p2.transpose()<<endl;
  return 0;
}
  

3.旋转的表达

手打公式真的太麻烦了，只能简单的写了，后面的证明题就用手写吧
1.证明：

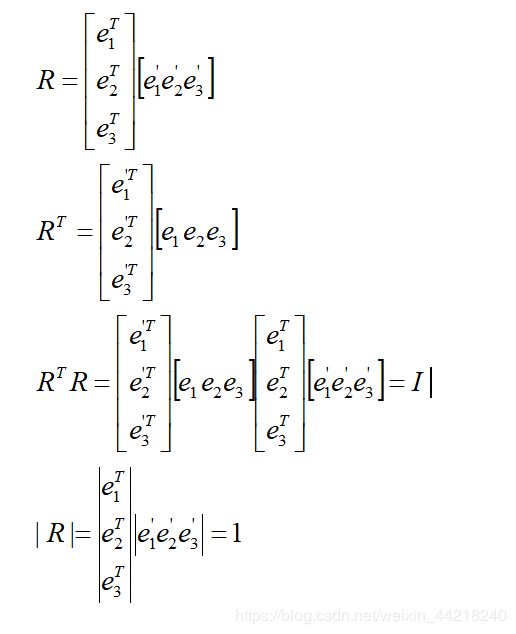
2.

四元数的实部是一维，虚部是三维

3.证明
本来想放上手写照片的，但是看上去不好看（颜控）搬运了他人的结果哈
方法一：

原文推导链接

方法2

4.罗德里格斯公式的证明

一个证明很详细的博客
https://www.cnblogs.com/jingrui/p/9712461.html

5.四元数运算性质的验证

1：

2：

6.熟悉 C++11

#include 
2 #include <vector>
3 #include <algorithm>
4
5 using namespace std;
6
7 class A {
8 public:
9 A(const int& i ) : index(i) {}
10 int index = 0;
11 };
12
13 int main() {
14 A a1(3), a2(5), a3(9);
15 vector<A> avec{a1, a2, a3};
16 std::sort(avec.begin(), avec.end(), [](const A&a1, const A&a2) {return a1.index<a2.index;});
17 for ( auto& a: avec ) cout<<a.index<<" ";
18 cout<<endl;
19 return 0;
}

C++11新特性

序列for循环
在C++中for循环可以使用类似java的简化的for循环，可以用于遍历数组，容器，string以及由begin和end函数定义的序列（即有Iterator）。
新的关键字auto
C++11中引入auto第一种作用是为了自动类型推导
auto的自动类型推导，用于从初始化表达式中推断出变量的数据类型。通过auto的自动类型推导，可以大大简化我们的编程工作，auto实际上实在编译时对变量进行了类型推导，所以不会对程序的运行效率造成不良影响。另外，似乎auto并不会影响编译速度，因为编译时本来也要右侧推导然后判断与左侧是否匹配。
Lambda表达式
lambda表达式类似Javascript中的闭包，它可以用于创建并定义匿名的函数对象，以简化编程工作。
Lambda的语法如下：
[函数对象参数]（操作符重载函数参数）->返回值类型{函数体}

更加优雅的初始化方法
在引入C++11之前，只有数组能使用初始化列表，其他容器想要使用初始化列表，只能用以下方法：

终于完成这一节了，数学的内容好多呀，C++11还需要多看看。（最后检查的时候发现把图片都粘错了位置，还好看到了）