机器学习系列22-无监督学习之自编码器

Unsupervised Learning: Deep Auto-encoder

如果本文对你有帮助，请给我的github打个star叭，上面附有全系列目录和内容！
更多优质内容欢迎关注我的微信公众号“Sakura的知识库”：

文本介绍了自编码器的基本思想，与PCA的联系，从单层编码到多层的变化，在文字搜索和图像搜索上的应用，预训练DNN的基本过程，利用CNN实现自编码器的过程，加噪声的自编码器，利用解码器生成图像等内容

Introduction

Auto-encoder本质上就是一个自我压缩和解压的过程，我们想要获取压缩后的code，它代表了对原始数据的某种紧凑精简的有效表达，即降维结果，这个过程中我们需要：

• Encoder(编码器)，它可以把原先的图像压缩成更低维度的向量
• Decoder(解码器)，它可以把压缩后的向量还原成图像

注意到，Encoder和Decoder都是Unsupervised Learning，由于code是未知的，对Encoder来说，我们手中的数据只能提供图像作为NN的input，却不能提供code作为output；对Decoder来说，我们只能提供图像作为NN的output，却不能提供code作为input

因此Encoder和Decoder单独拿出一个都无法进行训练，我们需要把它们连接起来，这样整个神经网络的输入和输出都是我们已有的图像数据，就可以同时对Encoder和Decoder进行训练，而降维后的编码结果就可以从最中间的那层hidden layer中获取

Compare with PCA

实际上PCA用到的思想与之非常类似，PCA的过程本质上就是按组件拆分，再按组件重构的过程

在PCA中，我们先把均一化后的$x$根据组件$W$分解到更低维度的$c$，然后再将组件权重$c$乘上组件的反置$W^T$得到重组后的$\hat{x}$，同样我们期望重构后的$\hat{x}$与原始的$x$越接近越好

如果把这个过程看作是神经网络，那么原始的$x$就是input layer，重构$\hat{x}$就是output layer，中间组件分解权重$c$就是hidden layer，在PCA中它是linear的，我们通常又叫它瓶颈层(Bottleneck layer)

由于经过组件分解降维后的$c$，维数要远比输入输出层来得低，因此hidden layer实际上非常窄，因而有瓶颈层的称呼

对比于Auto-encoder，从input layer到hidden layer的按组件分解实际上就是编码(encode)过程，从hidden layer到output layer按组件重构实际上就是解码(decode)的过程

这时候你可能会想，可不可以用更多层hidden layer呢？答案是肯定的

Deep Auto-encoder

Multi Layer

对deep的自编码器来说，实际上就是通过多级编码降维，再经过多级解码还原的过程

此时：

• 从input layer到bottleneck layer的部分都属于$Encoder$
• 从bottleneck layer到output layer的部分都属于$Decoder$
• bottleneck layer的output就是自编码结果$code$

注意到，如果按照PCA的思路，则Encoder的参数$W_i$需要和Decoder的参数$W_i^T$保持一致的对应关系，这可以通过给两者相同的初始值并设置同样的更新过程得到，这样做的好处是，可以节省一半的参数，降低overfitting的概率

但这件事情并不是必要的，实际操作的时候，你完全可以对神经网络进行直接训练而不用保持编码器和解码器的参数一致

Visualize

下图给出了Hinton分别采用PCA和Deep Auto-encoder对手写数字进行编码解码后的结果，从784维降到30维，可以看出，Deep的自编码器还原效果比PCA要更好

如果将其降到二维平面做可视化，不同颜色代表不同的数字，可以看到

• 通过PCA降维得到的编码结果中，不同颜色代表的数字被混杂在一起
• 通过Deep Auto-encoder降维得到的编码结果中，不同颜色代表的数字被分散成一群一群的

Text Retrieval

Auto-encoder也可以被用在文字处理上

比如我们要做文字检索，很简单的一个做法是Vector Space Model，把每一篇文章都表示成空间中的一个vector

假设查询者输入了某个词汇，那我们就把该查询词汇也变成空间中的一个点，并计算query和每一篇document之间的内积(inner product)或余弦相似度(cos-similarity)

注：余弦相似度有均一化的效果，可能会得到更好的结果

下图中跟query向量最接近的几个向量的cosine-similarity是最大的，于是可以从这几篇文章中去检索

实际上这个模型的好坏，就取决于从document转化而来的vector的好坏，它是否能够充分表达文章信息

Bag-of-word

最简单的vector表示方法是Bag-of-word，维数等于所有词汇的总数，某一维等于1则表示该词汇在这篇文章中出现，此外还可以根据词汇的重要性将其加权；但这个模型是非常脆弱的，对它来说每个词汇都是相互独立的，无法体现出词汇之间的语义(semantic)

Auto-encoder

虽然Bag-of-word不能直接用于表示文章，但我们可以把它作为Auto-encoder的input，通过降维来抽取有效信息，以获取所需的vector

同样为了可视化，这里将Bag-of-word降维到二维平面上，下图中每个点都代表一篇文章，不同颜色则代表不同的文章类型

如果用户做查询，就把查询的语句用相同的方式映射到该二维平面上，并找出属于同一类别的所有文章即可

在矩阵分解(Matrix Factorization)中，我们介绍了LSA算法，它可以用来寻找每个词汇和每篇文章背后的隐藏关系(vector)，如果在这里我们采用LSA，并使用二维latent vector来表示每篇文章，得到的可视化结果如上图右下角所示，可见效果并没有Auto-encoder好

Similar Image Search

Auto-encoder同样可以被用在图像检索上

以图找图最简单的做法就是直接对输入的图片与数据库中的图片计算pixel的相似度，并挑出最像的图片，但这种方法的效果是不好的，因为单纯的pixel所能够表达的信息太少了

我们需要使用Auto-encoder对图像进行降维和特征提取，并在编码得到的code所在空间做检索

下图展示了Encoder的过程，并给出了原图与Decoder后的图像对比

这么做的好处如下：

• Auto-encoder可以通过降维提取出一张图像中最有用的特征信息，包括pixel与pixel之间的关系
• 降维之后数据的size变小了，这意味着模型所需的参数也变少了，同样的数据量对参数更少的模型来说，可以训练出更精确的结果，一定程度上避免了过拟合的发生
• Auto-encoder是一个无监督学习的方法，数据不需要人工打上标签，这意味着我们只需简单处理就可以获得大量的可用数据

下图给出了分别以原图的pixel计算相似度和以auto-encoder后的code计算相似度的两种方法在图像检索上的结果，可以看到，通过pixel检索到的图像会出现很多奇怪的物品，而通过code检索到的图像则都是人脸

可能有些人脸在原图的pixel上看起来并不像，但把它们投影到256维的空间中却是相像的，可能在投影空间中某一维就代表了人脸的特征，因此能够被检索出来

Pre-training DNN

在训练神经网络的时候，我们一般都会对如何初始化参数比较困扰，预训练(pre-training)是一种寻找比较好的参数初始化值的方法，而我们可以用Auto-encoder来做pre-training

以MNIST数据集为例，我们对每层hidden layer都做一次auto-encoder，使每一层都能够提取到上一层最佳的特征向量

为了方便表述，这里用$x-z-x$来表示一个自编码器，其中$x$表述输入输出层的维数，$z$表示隐藏层的维数

• 首先使input通过一个$784-1000-784$的自编码器，当该自编码器训练稳定后，就把参数$W^1$固定住，然后将数据集中所有784维的图像都转化为1000维的vector

  注意：这里做的不是降维而是升维，当编码后的维数比输入维数要高时，需要注意可能会出现编码前后原封不动的情况，为此需要额外加一个正则项，比如L1 regularization，强迫使code的分布是分散的

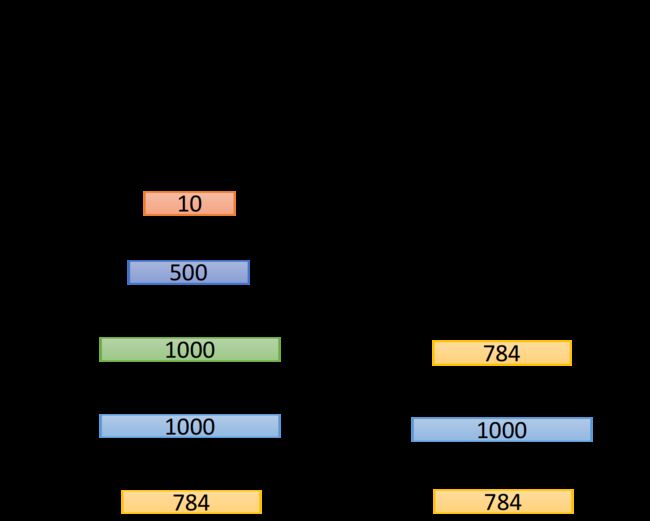
• 接下来再让这些1000维的vector通过一个$1000-1000-1000$的编码器，当其训练稳定后，再把参数$W^2$固定住，对数据集再做一次转换

• 接下来再用转换后的数据集去训练第三个$1000-500-1000$的自编码器，训练稳定后固定$W^3$，数据集再次更新转化为500维

• 此时三个隐藏层的参数$W^1$、$W^2$、$W^3$就是训练整个神经网络时的参数初始值

• 然后随机初始化最后一个隐藏层到输出层之间的参数$W^4$

• 再用反向传播去调整一遍参数，因为$W^1$、$W^2$、$W^3$都已经是很好的参数值了，这里只是做微调，这个步骤也因此得名为Find-tune

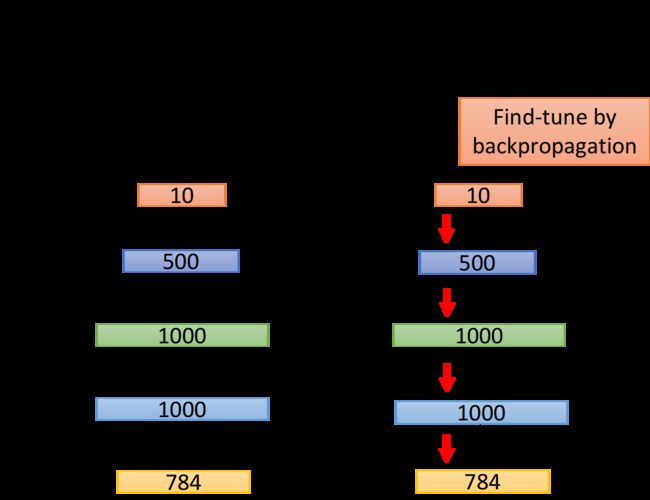
由于现在训练机器的条件比以往更好，因此pre-training并不是必要的，但它也有自己的优势

如果你只有大量的unlabeled data和少量的labeled data，那你可以先用这些unlabeled data把$W^1$、$W^2$、$W^3$先初始化好，最后再用labeled data去微调$W^1$~$W^4$即可

因此pre-training在有大量unlabeled data的场景下(如半监督学习)是比较有用的

CNN

CNN as Encoder

处理图像通常都会用卷积神经网络CNN，它的基本思想是交替使用卷积层和池化层，让图像越来越小，最终展平，这个过程跟Encoder编码的过程其实是类似的

理论上要实现自编码器，Decoder只需要做跟Encoder相反的事即可，那对CNN来说，解码的过程也就变成了交替使用去卷积层和去池化层即可

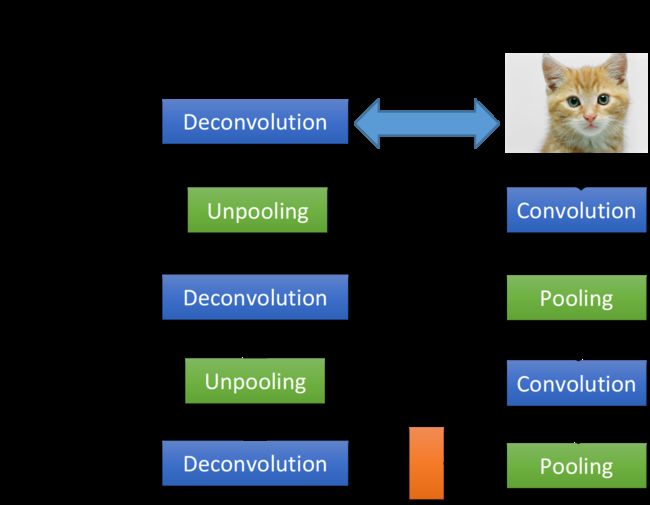
那什么是去卷积层(Deconvolution)和去池化层(Unpooling)呢？

Unpooling

做pooling的时候，假如得到一个4×4的matrix，就把每4个pixel分为一组，从每组中挑一个最大的留下，此时图像就变成了原来的四分之一大小

如果还要做Unpooling，就需要提前记录pooling所挑选的pixel在原图中的位置，下图中用灰色方框标注

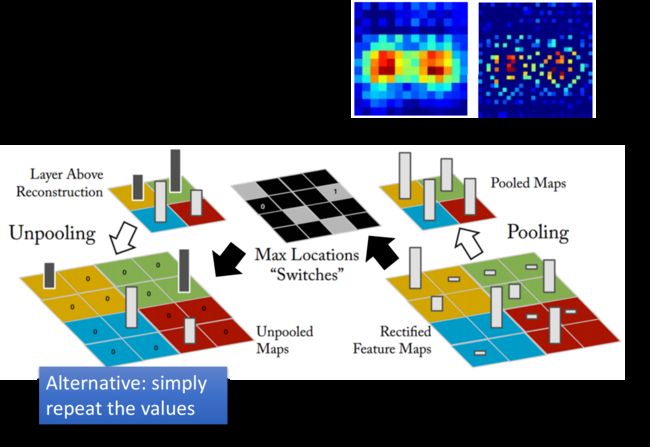
然后做Unpooling，就要把当前的matrix放大到原来的四倍，也就是把2×2 matrix里的pixel按照原先记录的位置插入放大后的4×4 matrix中，其余项补0即可

当然这不是唯一的做法，在Keras中，pooling并没有记录原先的位置，做Unpooling的时候就是直接把pixel的值复制四份填充到扩大后的matrix里即可

Deconvolution

实际上，Deconvolution就是convolution

这里以一维的卷积为例，假设输入是5维，过滤器(filter)的大小是3

卷积的过程就是每三个相邻的点通过过滤器生成一个新的点，如下图左侧所示

在你的想象中，去卷积的过程应该是每个点都生成三个点，不同的点对生成同一个点的贡献值相加；但实际上，这个过程就相当于在周围补0之后再次做卷积，如下图右侧所示，两个过程是等价的

卷积和去卷积的过程中，不同点在于，去卷积需要补零且过滤器的weight与卷积是相反的：

• 在卷积过程中，依次是橙线、蓝线、绿线
• 在去卷积过程中，依次是绿线、蓝线、橙线

因此在实践中，做去卷积的时候直接对模型加卷积层即可

Other Auto-encoder

De-noising Auto-encoder

去噪自编码器的基本思想是，把输入的$x$加上一些噪声(noise)变成$x^{\prime }$，再对$x^{\prime }$依次做编码(encode)和解码(decode)，得到还原后的$y$

值得注意的是，一般的自编码器都是让输入输出尽可能接近，但在去噪自编码器中，我们的目标是让解码后的$y$与加噪声之前的$x$越接近越好

这种方法可以增加系统的鲁棒性，因为此时的编码器Encoder不仅仅是在学习如何做编码，它还学习到了如何过滤掉噪声这件事情

参考文献：Vincent, Pascal, et al. “Extracting and composing robust features with denoising autoencoders.” ICML, 2008.

Contractive Auto-encoder

收缩自动编码器的基本思想是，在做encode编码的时候，要加上一个约束，它可以使得：input的变化对编码后得到的code的影响最小化

这个描述跟去噪自编码器很像，只不过去噪自编码器的重点在于加了噪声之后依旧可以还原回原先的输入，而收缩自动编码器的重点在于加了噪声之后能够保持编码结果不变

参考文献：Rifai, Salah, et al. "Contractive auto-encoders: Explicit invariance during feature extraction.“ Proceedings of the 28th International Conference on Machine Learning (ICML-11). 2011.

Seq2Seq Auto-encoder

在之前介绍的自编码器中，输入都是一个固定长度的vector，但类似文章、语音等信息实际上不应该单纯被表示为vector，那会丢失很多前后联系的信息

Seq2Seq就是为了解决这个问题提出的，具体内容将在RNN部分介绍

Generate

在用自编码器的时候，通常是获取Encoder之后的code作为降维结果，但实际上Decoder也是有作用的，我们可以拿它来生成新的东西

以MNIST为例，训练好编码器之后，取出其中的Decoder，输入一个随机的code，就可以生成一张图像

假设将28×28维的图像通过一层2维的hidden layer投影到二维平面上，得到的结果如下所示，不同颜色的点代表不同的数字，然后在红色方框中，等间隔的挑选二维向量丢进Decoder中，就会生成许多数字的图像

此外，我们还可以对code加L2 regularization，以限制code分布的范围集中在0附近，此时就可以直接以0为中心去随机采取样本点，再通过Decoder生成图像

观察生成的数字图像，可以发现横轴的维度表示是否含有圆圈，纵轴的维度表示是否倾斜