Task Schedule HDU - 3572(建图+最大流模版)

Task Schedule

题意： 工厂中有M台机器需要完成N个任务，第i个任务有三个属性：需要做满P天，不得早于S开始做，不得晚于E还没做完。并且每天机器每天只能做一个任务，每个任务每天只能由一个机器来做。需要求每一个任务是否都可以在期限内完成。

思路： 这个题目主要难点是需要想到这个可以用最大流来做，其次就是就怎么建图的问题，建好图之后就直接套最大流模版就可以了。

我们可以假设一个源点，把所有的任务发出来；然后汇点把这些任务接收，如果原点发出的任务量与汇点接收的任务量相等的话，那么证明所有的任务是可以完成的，反则反之。

所以怎么设置源点和汇点之间的约束条件就是解决问题的关键。

以 样例1 为例：

1、首先从源点S出发，那么将每个任务分开，就可以得到如图这样的连接，这样任务就可以从源点发出。

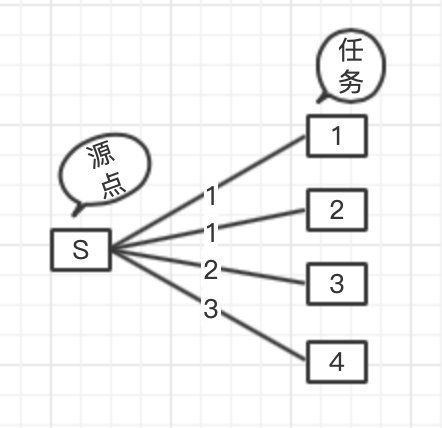
2、每个任务需要在指定的日期区间内完成，所以将每个任务连入指定的日期区间之中，这个处理可以把所有的天数都列举出来。权值全部都为1，因为这样才能满足每个任务只能在一天在一台机器上做。

3、将这些日期的区间全部汇集到汇点去，但是需要有一个限制，每一天最多最多能提交的任务也就是机器的台数，所以权值需要限制在m。

这样看每个点和每一条边就很直观了，逻辑上的图就建好了。找到源点到所有任务再到指定日期区间的增广路，判断从源点出来的任务量和汇点接收的任务量是否相等就可以知道每个任务是否都按时完成了。也就是为什么建好图这个题目就成模版题了的原因。

现在就需要将图中的点体现在程序中，像上图中的点坐标很容易发现是有冲突的，这样建图会出大问题，我这样画也就是好理解一些。

这样就可以啦！

#include
#define INF 0x3f3f3f3f
using namespace std;
struct EDGE {
	int to, w, next;
} edge[1000000];
int cnt;
int head[2000];
int deep[2000];

void init() {
	cnt = 0;
	memset(head, -1, sizeof(head));
}

void addedge(int u, int v, int w) {
	edge[cnt].to=v; edge[cnt].w=w; edge[cnt].next=head[u]; head[u]=cnt++;
	edge[cnt].to=u; edge[cnt].w=0; edge[cnt].next=head[v]; head[v]=cnt++;
}

int bfs(int s, int t) {
	queue<int> q;
	memset(deep, 0, sizeof(deep));
	q.push(s);
	deep[s] = 1;
	int top;
	while(!q.empty()) {
		top = q.front();
		q.pop();
		for(int i = head[top];i+1; i = edge[i].next) {
			int v = edge[i].to;
			int w = edge[i].w;
			if(!deep[v]&&w) {
				deep[v] = deep[top]+1;
				q.push(v);
			}
		}
	}
	return deep[t];
}

int dfs(int s, int t, int inflow) {
	if(s==t) return inflow;
	int acflow=0;
	for(int i=head[s]; i+1; i=edge[i].next) {
		if(edge[i].w && deep[s]+1 == deep[edge[i].to]) {
			int x = dfs(edge[i].to,t,min(inflow, edge[i].w));
			if(x>0) {
				acflow+=x; inflow-=x;edge[i].w -= x; edge[i^1].w += x;
				if(!inflow) break;
			}
		}
	}
	if(!acflow) deep[s] = -2;
	return acflow;
}

int dinic(int s,int t) {
	int f = 0;
	while(bfs(s,t)) f += dfs(s,t,INF);
	return f;
}

int main() {
	int _, n, m, cas = 0, p, s, e;
	scanf("%d", &_);
	while(_--) {
		init();
		scanf("%d %d", &n, &m);
		int l = INF, r = 0, sum = 0;
		for(int i = 1;i <= n; ++i) {
			scanf("%d %d %d", &p, &s, &e);
			sum += p;
			l = min(l, s); r = max(r, e);
			addedge(0, i, p);
			
			for(int j = s;j <= e; j++) {
				addedge(i, j+n, 1);
			}
		}
		
		int fin = r+n+1;
		for(int i = l; i <= r; ++i) {
			addedge(i+n, fin, m);
		}
		
		printf("Case %d: %s\n\n", ++cas, dinic(0, fin)==sum?"Yes":"No");
	}
}