基于Python的Kmeans聚类分析介绍及实践

基于Python的Kmeans聚类分析介绍及实践

• 这是一篇学习的总结笔记
• 参考自《从零开始学数据分析与挖掘》 [中]刘顺祥 著
• 完整代码及实践所用数据集等资料放置于：Github

聚类算法是依据已知的数据集，将高度相似的样本集中到各自的簇中。例如，借助于电商平台用户的历史交易数据，将用户划分为不同的价值等级（如VIP、高价值、潜在价值、低价值等）；依据经度、纬度、交通状况、人流量等数据将地图上的娱乐场所划分为不同的区块（如经济型、交通便捷型、安全型等）；利用中国各城市的经济、医疗状况等数据将其划分为几种不同的贫富差距等级（如划分一二三四线城市等）。
如上，聚类算法不仅可以将数据集实现分割，还可以用于异常点的检测，即远离任何簇的样本我们可以视为异常点（离群），而这些异常的样本往往在某些场景下我们要特别关注。如：①信用卡交易的异常，当用户频繁进行奢侈品的交易时可能意味着某种欺诈行为的出现（土豪请忽略）；②社交平台中的访问异常，当某个用户频繁地对网站进行访问时（如在1秒钟内访问了上千次），我们可以假设该用户在进行网络爬虫；③电商平台交易异常：一张银行卡被用于上百个ID的支付，并且这些交易订单的送货地址都在某个相近的区域，则可能暗示“黄牛”的出现。总之，我们有很大概率能从离群点中挖掘出我们所需要的信息。
聚类算法是比较典型的无监督学习算法，在数据挖掘领域，能实现聚类的算法有很多。本篇介绍其中的一种——Kmeans聚类算法，该算法利用距离远近的思想将目标数据划分为指定的k个簇，簇内样本越相似，表明聚类效果越好（同样我们尽可能使簇间样本不相似，以避免产生“模棱两可”的现象，这点我们在后面会进行介绍）。重要的内容如下：

• Kmeans聚类的思想和原理
• 如何利用数据本身选出合理的k个簇
• Kmeans聚类的应用实战

无监督学习

现实生活中常常会有这样的问题：缺乏足够的先验知识，因此难以人工标注类别或进行人工类别标注的成本太高。很自然地，我们希望计算机能代我们完成这些工作，或至少提供一些帮助。根据类别未知(没有被标记)的训练样本解决模式识别中的各种问题，称之为无监督学习。
——百度百科

Kmeans聚类

之所以称为Kmeans，是因为该算法可以将数据集划分为指定的k个簇，并且簇的中心点由各簇样本的均值计算所得。首先我们需要知道Kmeans实现聚类的思想和原理。

Kmeans的思想

Kmeans聚类算法的思路通俗易懂，通过不断计算各样本点与簇中心的距离，直到收敛为止，具体步骤如下：

1. 从数据中随机挑选k个样本点作为原始的簇中心
2. 计算剩余样本与簇中心的距离，并把各样本标记为离k个簇中心最近的类别
3. 重复计算各簇中样本点的均值，并以均值作为新的k个簇中心
4. 重复2、3步骤，直到簇中心的变化趋势趋于稳定，形成最终的k个簇

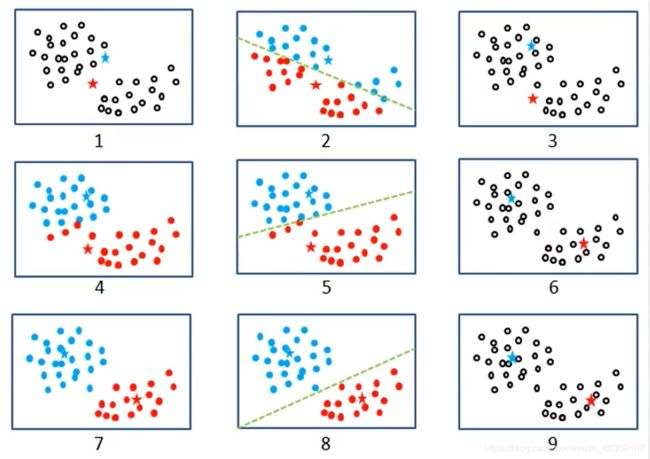
我们结合下图来理解此过程

对各个子图做详细说明如下：

1. 从样本点中随机挑选两个数据点作为初始的簇中心，如图中所示的两个五角星
2. 将其余样本点与这两个簇中心分别计算距离（距离的测度可以有多种，常见的有欧氏距离、曼哈顿距离等），然后将每个样本点划分到离簇中心（五角星）最近的簇中，即图中用虚线隔开的两部分
3. 计算两个簇内样本的均值，得到新的簇中心，即图中的两个新的五角星

以新的簇中心不断重复以上三个步骤，得到的簇中心会趋于稳定，最终得到理想的聚类效果，如图9所示。

Kmenas聚类算法的思想比较简单，Python提供了实现该算法的模块——sklearn，我们只需要调用其子模块cluster中的Kmeans类即可，该“类”的语法和参数含义如下：

Kmeans(n_clusters=8, init='k-means++', n_init=10, max_iter=300, tol=0.0001,
        precompute_distances='auto', verbose=0, random_state=None, 
        copy_x=True, n_jobs=1, algorithm='auto')

• n_clusters：用于指定聚类的簇数
• init：用于指定初始的簇中心的设置方法，如果为’k-means++’，则表示设置的初始簇中心相距较远；如果为’random’则表示从数据集中随机挑选k个样本作为初始簇中心；如果为数组，则表示用户指定具体的初始簇中心
• n_init：用于指定Kmeans算法的运行次数，每次运行时都会选择不同的初始簇中心，目的是防止算法收敛于局部最优，默认为10
• max_iter：用于指定单次运行的迭代次数，默认为300
• tol：用于指定算法的收敛阈值，默认为0.0001
• precompute_distances：bool类型参数，是否在算法运行之前计算样本之间的距离，默认为’auto’，表示当样本量与变量个数的乘积大于1200万时不计算样本之间的距离
• verbose：通过该参数设置算法返回日志信息的频度，默认为0，表示不输出日志信息；如果为1，就表示每隔一段时间返回日志信息
• random_state：用于指定随机数生成器的种子
• copy_X：bool类型参数，当参数precompute_distances为True时有效，如果该参数为True，就表示提前计算距离时不改变原始数据，否则会修改原始数据
• n_jobs：用于指定算法运行时的CPU数量，默认为1，如果为-1，就表示使用所有可用的CPU
• algorithm：用于指定Kmeans的实现算法，可以选择’auto’‘full’和’elkan’，默认为’auto’，表示自动根据数据特征选择运算的算法

Kmeans的原理

上面提到，对于指定的k个簇，簇内样本越相似，聚类效果越好，我们可以根据这个结论为Kmeans聚类算法构造目标函数。该目标函数的思想是：所有簇内样本的离差平方和之和达到最小。（我们可以这么理解：如果某个簇内样本很相似，则簇内的离差平方和会非常小（另一种理解是：簇内方差小）），对于所有簇而言，我们就是要寻求使得所有簇的离差平方和总和最小的划分。
根据上面思想，我们可以构造如下目标函数：$$J(c_1,c_2,...c_k)=\sum _{j=1}^k\sum _i^{n_j}(x_i-c_j{)}^2$$其中，$c_j$表示第$j$个簇的簇中心，$x_i$是第$j$个簇中的样本，$n_j$是第$j$个簇的样本总量。对于该目标函数而言，$c_j$是未知的参数，如果要求地目标函数的最小值，得先知道参数$c_j$的值。由于目标函数函数$J$为一个凸函数，我们可以通过求导的方式获取合理的参数$c_j$的值，具体步骤如下：
步骤①：对目标函数求导$$\frac{\partial J}{\partial c_j}=\sum _{j=1}^k\sum _i^{n_j}\frac{(x_i-c_j{)}^2}{\partial c_j}=\sum _i^{n_j}\frac{(x_i-c_j{)}^2}{\partial c_j}=\sum _{i=1}^{n_j}-2(x_i-c_j)$$如上，由于仅对目标函数的第$j$个簇中心$c_j$求偏导，因此其他簇的离差平方和的倒数均为0，进而求偏导结果只保留第$j$个簇的离差平方和的导数。
步骤②：令导函数等于0$$\sum _{i=1}^{n_j}-2(x_i-c_j)=0$$$$n_j{c}_j-\sum _{i=1}^{n_j}{x}_i=0$$$$c_j=\frac{{\sum }_{i=1}^{n_j}{x}_i}{n_j}={\mu }_j$$如上推导结果所示，只有当簇中心$c_j$为簇内样本均值时，目标函数才会达到最小值，获得稳定的簇。而通过观察我们发现，推导出来的簇中心正好与Kmeans聚类思想中的样本均值相吻合。
上面的推导都是基于已知的$k$个簇运算出来的最佳的簇中心，如果聚类之前不知道应该聚为几类时，如何根据数据本身确定较为合理的k值呢？
一种极端的处理思想是：当簇的个数与样本个数一致时（即每个样本代表一个簇），就可以得到最小的离差平方和总和：0。这样划分确实能得到最小值，我们可以这么认为：簇被划分得越细，离差平方和总和会越小（这一点可以很容易想到），但是这样的簇不一定是合理的（每个样本作为一个簇相当于没有划分，结果无意义）。
所以下面我们介绍几种常用的确定k值的方法。

最佳k值的确定

对于Kmeans算法来说，如何确定k值是一个至关重要的问题，为了解决这个问题，通常采用探索法，即给定不同的k值的情况下，对比某些评估指标的变动情况，进而选择一个比较合理的k值。下面我们介绍三种常用的评估方法：簇内离差平方和拐点法、轮廓系数法和间隔统计量法。

拐点法

簇内离差平方和拐点法的思想很简单，就是在不同的k值下计算簇内的离差平方和，然后通过可视化的方法找到“拐点”所对应的k值。
前文所介绍的Kmeans聚类算法的目标函数$J$，随着簇数量的增加，簇中的样本量就会越来越少，进而簇内离差平方和也会越来越小。通过可视化的方法，重点放在观察斜率的变化，当斜率由大突然变小，并且之后的斜率变化缓慢，则认为突然变化的点就是我们所要寻找的目标点（拐点之后随着簇数k的增加，聚类效果不再有大的变化，所以再增加簇数量意义不大）。
我们先随机生成三组二元正态分布数据作为测试数据集，然后基于该数据绘制散点图，具体代码如下：

# 导入第三方包
import pandas as pd
import numpy as np  
import matplotlib.pyplot as plt

# 随机生成三组二元正态分布随机数 
np.random.seed(1234)
mean1 = [0.5, 0.5]
cov1 = [[0.3, 0], [0, 0.3]]
x1, y1 = np.random.multivariate_normal(mean1, cov1, 1000).T

mean2 = [0, 8]
cov2 = [[1.5, 0], [0, 1]]
x2, y2 = np.random.multivariate_normal(mean2, cov2, 1000).T

mean3 = [8, 4]
cov3 = [[1.5, 0], [0, 1]]
x3, y3 = np.random.multivariate_normal(mean3, cov3, 1000).T

# 绘制三组数据的散点图
plt.scatter(x1,y1)
plt.scatter(x2,y2)
plt.scatter(x3,y3)
# 显示图形
plt.show()

如上图所示，测试数据集呈现三个簇，接下来基于这个虚拟数据集，使用拐点法，绘制簇的个数与总的离差平方和之间的折线图，确定应该聚为几类比较合适，具体代码如下：

# 构造自定义函数，用于绘制不同k值和对应总的簇内离差平方和的折线图
def k_SSE(X, clusters):
    # 选择连续的K种不同的值
    K = range(1,clusters+1)
    # 构建空列表用于存储总的簇内离差平方和
    TSSE = []
    for k in K:
        # 用于存储各个簇内离差平方和
        SSE = []
        kmeans = KMeans(n_clusters=k)
        kmeans.fit(X)
        # 返回簇标签
        labels = kmeans.labels_
        # 返回簇中心
        centers = kmeans.cluster_centers_
        # 计算各簇样本的离差平方和，并保存到列表中
        for label in set(labels):
            SSE.append(np.sum((X.loc[labels == label,]-centers[label,:])**2))
        # 计算总的簇内离差平方和 
        TSSE.append(np.sum(SSE))

    # 中文和负号的正常显示
    plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
    plt.rcParams['axes.unicode_minus'] = False
    # 设置绘图风格
    plt.style.use('ggplot')
    # 绘制K的个数与GSSE的关系
    plt.plot(K, TSSE, 'b*-')
    plt.xlabel('簇的个数')
    plt.ylabel('簇内离差平方和之和')
    # 显示图形
    plt.show()

# 将三组数据集汇总到数据框中
X = pd.DataFrame(np.concatenate([np.array([x1,y1]),np.array([x2,y2]),np.array([x3,y3])], axis = 1).T)
# 自定义函数的调用
k_SSE(X, 15)

生成图形如下：

如上图所示，当簇的个数为3时形成了一个明显的“拐点”，因为k值从1到3时，折线的斜率都比较大，但是斜率为4的时候突然就降低了很多，并且之后的簇对应的斜率都变动很小。
所以，合理的k值应该为3，与虚拟的三个簇数据是吻合的。

轮廓系数法

该方法综合考虑了簇的密集性与分散性两个信息，如果数据集被分割为理想的k个簇，那么对应的簇内样本会很密集，而簇间样本会很分三，轮廓系数的计算公式如下：$$S(i)=\frac{b(i)-a(i)}{max(a(i),b(i))}$$其中，$a(i)$体现了簇内的密集性，代表样本$i$与同簇内其他样本点距离的平均值；$b(i)$反映了簇间的分散性，其计算过程是：样本$i$与其他非同簇样本点距离的平均值，然后从平均值中挑选出最小值。
为了方便理解，我们以下面图形加以说明：

如图，数据集被拆分为4各簇，样本$i$对应的$a(i)$就是所有$C_1$中其他样本点与样本$i$的距离平均值；样本$i$对应的$b(i)$值分两步计算：①计算该点分别到$C_2$、$C_3$和$C_4$中样本点的平均距离，然后将三个平均值中的最小值作为$b(i)$的度量。
通过公式可知，当$S(i)$接近于-1时，说明样本$i$分配不合理，需要将其分配到其他簇中；当$S(i)$近似为0时，说明样本$i$落在了模糊地带（即可能处于两个簇的中间部分，所以划分到哪个簇都可以），即簇的边界处；当$S(i)$近似为1时，说明样本$i$的分配是合理的。
上面步骤计算的仅仅是样本$i$的轮廓系数，最终需要对所有点的轮廓系数求平均值，得到的结果才是对应$k$个簇的总轮廓系数。
上诉所阐述的思想比较简单易懂，但是其计算的复杂度比较高，当样本量比较多时，运行时间会十分长。
有关轮廓系数的计算，我们可以直接调用sklearn子模块metris中的函数silhouette_score。该函数接受的聚类簇数必须大于或等于2，下面基于该函数重新自定义一个函数，用于绘制不同$k$值下对应轮廓系数的折线图，具体代码如下所示：

# 构造自定义函数，用于绘制不同k值和对应轮廓系数的折线图
def k_silhouette(X, clusters):
    K = range(2,clusters+1)
    # 构建空列表，用于存储个中簇数下的轮廓系数
    S = []
    for k in K:
        kmeans = KMeans(n_clusters=k)
        kmeans.fit(X)
        labels = kmeans.labels_
        # 调用字模块metrics中的silhouette_score函数，计算轮廓系数
        S.append(metrics.silhouette_score(X, labels, metric='euclidean'))

    # 中文和负号的正常显示
    plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
    plt.rcParams['axes.unicode_minus'] = False
    # 设置绘图风格
    plt.style.use('ggplot')    
    # 绘制K的个数与轮廓系数的关系
    plt.plot(K, S, 'b*-')
    plt.xlabel('簇的个数')
    plt.ylabel('轮廓系数')
    # 显示图形
    plt.show()
    
# 自定义函数的调用
k_silhouette(X, 15)

生成的图形如下：

如上图所示，我们利用之前构造的虚拟数据，绘制了不同$k$值下对应的轮廓系数图，由图可知，当$k$值等于3时，轮廓系数最大，且比较接近于1，说明应该把数据聚为3类比较合理，同样，与原始数据集的3个簇是吻合的。

间隔量统计法

间隔量统计法（Gap Statistic算法）可以适用于任何聚类算法，其基本思想是通过比较参照数据集与实际数据集在相同k值下的聚类效果。
算法的基本过程是：首先在样本所在区域内按照均匀分布随机地产生和原始样本数一样多的随机样本，并对这个随机样本做k均值，然后与实际样本进行比较。实际上可以看做是随机样本的损失和实际样本的损失之差。假设实际样本对应的最佳簇数是K，那么实际样本的损失应该相对较小，随机样本损失与实际样本损失之差也响应的达到最大，随机样本的损失和实际样本的损失之差取得最大值所对应的K值就是最佳簇数。
有关间隔量统计法（Gap Statistic算法）的具体实现我们在这里不做介绍，实现代码已放置于git，读者可以下载进行测试，有兴趣的读者也可以自行查找其他资料。

Kmeans聚类的应用

在进行Kmeans聚类时我们要注意两点：

• 聚类前必须指定具体的簇数量k值，如果k值是已知的（通过散点图可大致观察，或某些数据本身具有较为明确的类别划分），就可直接调用cluster子模块中的Kmeans类，对数据集进行聚类分析；如果k值是未知知的，可以根据行业经验或前面介绍的三种方法去确定一个较为合理的k值。
• 是否需要对原始数据集做标准化处理，由于Kmeans的思想是基于点之间的距离来实现“物以类聚”的，所以，如果数据集存在量纲上的差异，就必须对其进行标准化的预处理。

数据标准化

在数据分析之前，我们通常需要先将数据标准化（normalization），利用标准化后的数据进行数据分析。数据标准化也就是统计数据的指数化。数据标准化处理主要包括数据同趋化处理和无量纲化处理两个方面。数据同趋化处理主要解决不同性质数据问题，对不同性质指标直接加总不能正确反映不同作用力的综合结果，须先考虑改变逆指标数据性质，使所有指标对测评方案的作用力同趋化，再加总才能得出正确结果。数据无量纲化处理主要解决数据的可比性。数据标准化的方法有很多种，常用的有“最小—最大标准化”、“Z-score标准化”和“按小数定标标准化”等。经过上述标准化处理，原始数据均转换为无量纲化指标测评值，即各指标值都处于同一个数量级别上，可以进行综合测评分析。
——百度词条

数据标准化在Python中可以借助sklearn子模块preprocessing中的scale函数或minmax_scale实现，上述两个函数的标准化公式如下：$$scale=\frac{x-mean(x)}{std(x)}$$$$minma{x}_{s}cale=\frac{x-min(x)}{max(x)-min(x)}$$上式中$mean(x)$为变量$x$的平均值，$std(x)$为变量$x$的标准差，$max(x)$和$min(x)$分别为变量$x$的最大值与最小值。（第一种方法会将变量压缩为均值为0、标准差为1的无量纲数据，第二种方法会将变量压缩为[0,1]之间的无量纲数据。 ）
接下来我们基于上诉理论，通过对两个实际数据集的实践来进一步理解Kmeans聚类的思想及实际操作步骤。

iris数据集的聚类

iris数据集经常被用于数据挖掘的项目案例之中，其反映了3种鸢尾花在花萼长度、宽度和花瓣长度、宽度之间的差异，一共包含150个观测值。首先我们读取数据集并观测其前五行数据，输出如下：

In [13]: iris = pd.read_csv(r'iris.csv')

In [14]: iris.head()
Out[14]:
   Sepal_Length  Sepal_Width  Petal_Length  Petal_Width Species
0           5.1          3.5           1.4          0.2  setosa
1           4.9          3.0           1.4          0.2  setosa
2           4.7          3.2           1.3          0.2  setosa
3           4.6          3.1           1.5          0.2  setosa
4           5.0          3.6           1.4          0.2  setosa

如上数据所示，前4个变量为数值型变量，下面我们利用数据集中的四个数值型变量，对该数据集进行聚类。
数据集的前四个变量分别是花萼长度、宽度和花瓣长度、宽度之间，通过观察我们发现，它们之间没有量纲上的差异，故无需对其做标准化处理；最后一个变量为鸢尾花所属的种类。在聚类之前，我们可以先通过原本的数据集最后一个变量来观察应该聚为几类，具体代码如下：

In [15]: set(iris['Species'])
Out[15]: {'setosa', 'versicolor', 'virginica'}

如上结果所示，我们应该将数据集聚为3类，所以Kmeans中n_clusters参数设置为3，然后进行聚类，具体代码如下：

# 提取出用于建模的数据集X
X = iris.drop(labels = 'Species', axis = 1)
# 构建Kmeans模型
kmeans = KMeans(n_clusters = 3)
kmeans.fit(X)

接下来我们统计聚类的结果，具体代码及结果如下：

In [17]: # 聚类结果标签
     ...: X['cluster'] = kmeans.labels_
     ...: # 各类频数统计
     ...: X.cluster.value_counts()
Out[17]:
1    62
0    50
2    38
Name: cluster, dtype: int64

如上结果所示，通过设置参数n_clusters为3就可以非常方便地得到三个簇，并且我们对每个簇的样本进行统计，发现各簇的样本量分别为62、50和38。
首先我们可以通过输出原始数据集中的类别划分来对比聚簇效果的好坏，具体如下：

In [18]: iris.Species.value_counts()
Out[18]:
setosa        50
versicolor    50
virginica     50
Name: Species, dtype: int64

如上，原始数据集将鸢尾花划分为三类，并且每一类均有50个值，这与我们通过Kmeans聚类划分出来的三个簇各自的值差异不大，所以聚类效果还是较为理想的。
我们还可以通过绘制花瓣长度与宽度的散点图，对比原始数据集的三类和建模后的三类差异。

# 导入第三方模块
import seaborn as sns

# 三个簇的簇中心
centers = kmeans.cluster_centers_
# 绘制聚类效果的散点图
sns.lmplot(x = 'Petal_Length', y = 'Petal_Width', hue = 'cluster', markers = ['^','s','o'], 
           data = X, fit_reg = False, scatter_kws = {'alpha':0.8}, legend_out = False)
plt.scatter(centers[:,2], centers[:,3], marker = '*', color = 'black', s = 130)
plt.xlabel('花瓣长度')
plt.ylabel('花瓣宽度')
# 图形显示
plt.show()

# 增加一个辅助列，将不同的花种映射到0,1,2三种值，目的方便后面图形的对比
iris['Species_map'] = iris.Species.map({'virginica':0,'setosa':1,'versicolor':2})
# 绘制原始数据三个类别的散点图
sns.lmplot(x = 'Petal_Length', y = 'Petal_Width', hue = 'Species_map', data = iris, markers = ['^','s','o'],
           fit_reg = False, scatter_kws = {'alpha':0.8}, legend_out = False)
plt.xlabel('花瓣长度')
plt.ylabel('花瓣宽度')
# 图形显示
plt.show()

生成的两个图形如下：

如上图所示，左图为聚类效果的散点图，其中五角星为每个簇的簇中心；右图为原始分类的散点图。从图中可知，聚类算法将标记为1的所有花聚为一簇，与原始数据集吻合；对于标记为0和2的花种，聚类算法存在一定的错误分割，但绝大多数样本的聚类效果还是与原始数据集比较一致的。
接下来，为了更加直观地对比三个簇内样本之间的差异，我们使用雷达图对四个维度的信息进行展现，绘图所使用的数据为簇中心。雷达图的绘制需要导入pygal模块，绘图代码如下：

# 导入第三方模块
import pygal
# 调用Radar这个类，并设置雷达图的填充，及数据范围
radar_chart = pygal.Radar(fill = True)
# 添加雷达图各顶点的名称
radar_chart.x_labels = ['花萼长度','花萼宽度','花瓣长度','花瓣宽度']

# 绘制三个雷达图区域，代表三个簇中心的指标值
radar_chart.add('C1', centers[0])
radar_chart.add('C2', centers[1])
radar_chart.add('C3', centers[2])
# 保存图像
radar_chart.render_to_file('radar_chart.svg')

形成的图形如下：

如上图所示，对于$C_1$类的鸢尾花而言，其花萼长度及花瓣长度与宽度都是最大的；而$C_2$类的鸢尾花，对应的三个值都是最小的；$C_3$类的鸢尾花，三个指标的平均值恰好落在$C_1$和$C_2$之间。
pygal模块绘制的雷达图无法通过plt.show的方式进行显示，故选择svg的保存格式。

NBA球员数据集的聚类

如上我们所讲的关于鸢尾花的聚类例子中，在聚类之前我们知道数据应该聚为三类，所以直接调用Kmeans类完成聚类。接下来我们来看一个不知道应该聚为几类的数据集。
我们给出一个未知分类个数的数据集——NBA球员数据集，前面我们讲过，对于不知道应该聚为几簇的数据集，我们首先要运用探索的方法获知理想的簇数k值，然后才可以进行聚类操作。
该数据集一共包含286名球员的历史投篮记录，这些记录包括球员姓名、所属球队、得分、命中率等信息。首先我们读入数据并观察其前五行数据：

In [187]: players = pd.read_csv(r'players.csv')

In [188]: players.head()
Out[188]:
   排名         球员  球队    得分        命中-出手    命中率       命中-三分  三分命中率      命中-罚球  罚球命中率  场次  上场时间
0   1     詹姆斯-哈登  火箭  31.9   9.60-21.10  0.454  4.20-10.70  0.397  8.50-9.90  0.861  30  36.1
1   2  扬尼斯-阿德托昆博  雄鹿  29.7  10.90-19.90  0.545   0.50-1.70  0.271  7.50-9.80  0.773  28  38.0
2   3    勒布朗-詹姆斯  骑士  28.2  10.80-18.80  0.572   2.10-5.10  0.411  4.50-5.80  0.775  32  37.3
3   4     斯蒂芬-库里  勇士  26.3   8.30-17.60  0.473   3.60-9.50  0.381  6.00-6.50  0.933  23  32.6
4   4     凯文-杜兰特  勇士  26.3   9.70-19.00  0.510   2.50-6.30  0.396  4.50-5.10  0.879  26  34.8

如上输出所示，得分、命中率、三分命中率、罚球命中率、场次和上场时间都为数值型变量，并且其中某些数据之间的量纲不一致，故需要对数据做标准化处理。这里我们选取得分、命中率、三分命中率和罚球命中率4个维度的信息用于球员聚类的依据。
首先我们绘制球员得分与命中率之间的散点图，观察数据的分布情况，方便我们与聚类结果做对比，具体代码如下：

# 绘制得分与命中率的散点图
sns.lmplot(x = '得分', y = '命中率', data = players, 
           fit_reg = False, scatter_kws = {'alpha':0.8, 'color': 'steelblue'})
plt.show()

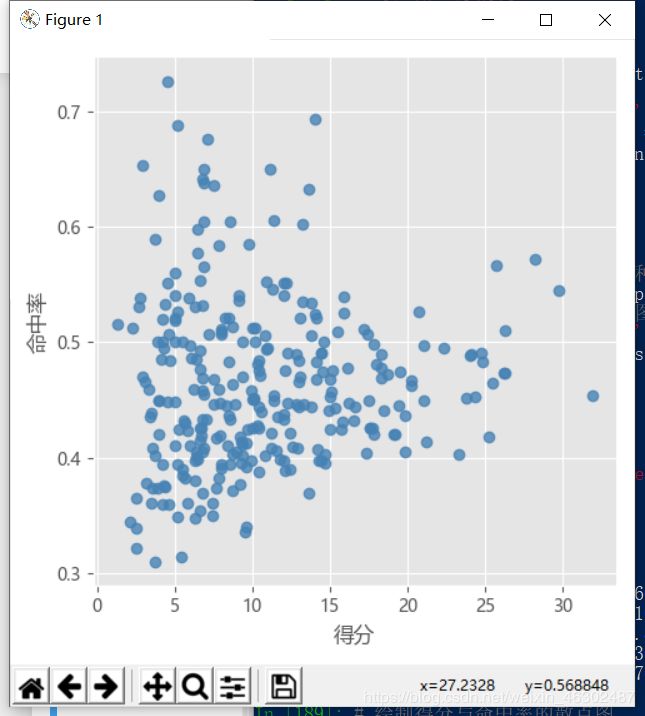
显示的散点图如下：

如上图所示，我们无法通过肉眼观察，直接得出对这286名球员应该聚为几类，下面我们利用前面所讲的几种方法中已实现的拐点法和轮廓系数法，来帮助我们得出最佳的k值。
一、拐点法得出最佳k值：

from sklearn import preprocessing
# 数据标准化处理
X = preprocessing.minmax_scale(players[['得分','罚球命中率','命中率','三分命中率']])
# 将数组转换为数据框
X = pd.DataFrame(X, columns=['得分','罚球命中率','命中率','三分命中率'])
# 使用拐点法选择最佳的K值
k_SSE(X, 15)

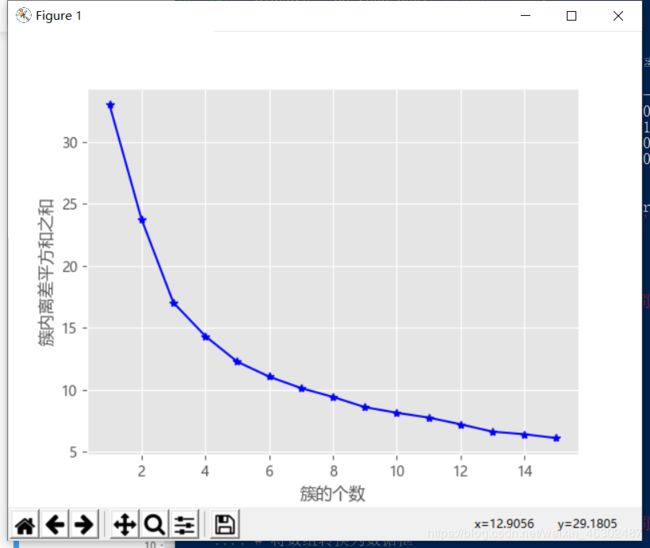
生成图形如下：

如上图所示，随着簇数的增加，簇内离差平方和的总和在不断减小，当k值在4附近时，折线斜率的变动就不是很大了，故我们可以选择的k值是3、4.为了进一步确定合理的k值，我们再参考轮廓系数法所得到的结果：

# 使用轮廓系数选择最佳的K值
k_silhouette(X, 15)

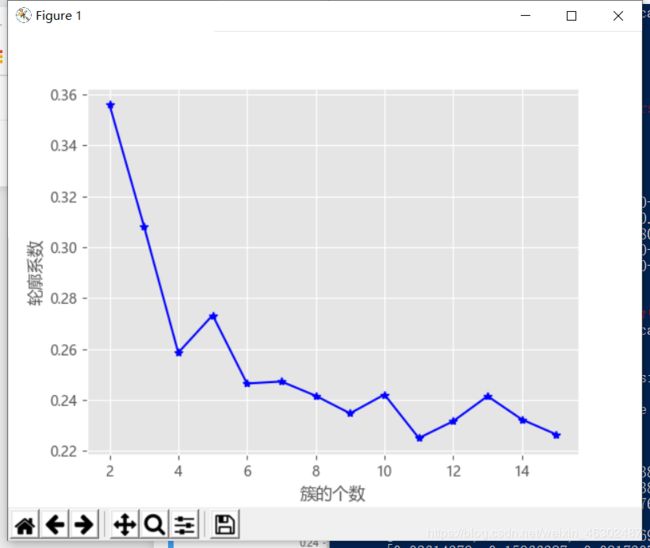
生成图形如下：

如上轮廓系数图所示，当k值为2时对应的轮廓系数最大，k值为3时次之，我们综合考虑上面两种方法进行探索的出来的k值，将最佳聚类个数k值确定为3.
接下来我们就使用上面所求出的最佳k值对NBA球员数据集进行聚类，具体如下：

# 将球员数据集聚为3类
kmeans = KMeans(n_clusters = 3)
kmeans.fit(X)

基于聚类好的数据，我们重新绘制球员得分与命中率之间的散点图，来更加直观地看出聚类的结果及效果，具体代码如下：

# 将聚类结果标签插入到数据集players中
players['cluster'] = kmeans.labels_
# 构建空列表，用于存储三个簇的簇中心
centers = []
for i in players.cluster.unique():
    centers.append(players.loc[players.cluster == i,['得分','罚球命中率','命中率','三分命中率']].mean())
# 将列表转换为数组，便于后面的索引取数
centers = np.array(centers)

# 绘制散点图
sns.lmplot(x = '得分', y = '命中率', hue = 'cluster', data = players, markers = ['^','s','o'],
           fit_reg = False, scatter_kws = {'alpha':0.8}, legend = False)
# 添加簇中心
plt.scatter(centers[:,0], centers[:,2], c='k', marker = '*', s = 180)
plt.xlabel('得分')
plt.ylabel('命中率')
# 图形显示
plt.show()

结果如下图所示：

结果如上图所示，下面我们对聚类的结果进行分析，图中五角星代表各个簇的中心点。
对比正方形和圆形的点，它们之间的差异主要体现在命中率上，正方形所代表的球员得分和命中率均较低（说明该类球员整体实力较差），命中率普遍在50%以下；而圆形代表的球员属于低得分高命中率型（说明该类球员可能是新秀球员，新秀球员实力较强但上场时间较少）。
再对比正方形和三角形的点，它们的差异主要体现在得分上，三角形所代表的点属于高得分低命中率型（说明该类球员的上场时间及出手次数比较多）。
当然，一个好的球员要求命中率与得分两项数值都比较优秀，即高得分高命中率，如图中左上角的几个点所代表的球员。
需要注意的是，由于我们在进行聚类之前对数据做了标准化处理，因此图中的簇中心不能直接用cluater_centers_方法获得，因为该方法此时返回的是数据标准化后的簇中心。故在代码中我们需要在原始数据集中计算出簇中心，并将其以五角星的标记添加到散点图中。
最后我们来看一下三类球员的雷达图，比对这三类球员在四个指标上的差异。由于四个维度存在量纲上的不一致，故我们需要使用标准化后的簇中心来绘制雷达图，具体代码如下：

# 雷达图
# 调用模型计算出来的簇中心
centers_std = kmeans.cluster_centers_
# 设置填充型雷达图
radar_chart = pygal.Radar(fill = True)
# 添加雷达图各顶点的名称
radar_chart.x_labels = ['得分','罚球命中率','命中率','三分命中率']

# 绘制雷达图代表三个簇中心的指标值
radar_chart.add('C1', centers_std[0])
radar_chart.add('C2', centers_std[1])
radar_chart.add('C3', centers_std[2])
# 保存图像
radar_chart.render_to_file('radar_chart.svg')

生成的雷达图如下：

如上雷达图所示，三个类别的球员在各个维度上存在着差异，以$C_2$和$C_3$为例，他们的平均得分并没有显著差异，但是$C_3$的命中率却明显比$C_2$高很多；再从平均的罚球命中率与三分命中率来看，$C_2$类的球员普遍要比$C_3$类的球员要强一些。

Kmeans聚类的注意事项

上面我们通过两个案例详细介绍了有关Kmeans聚类的应用实践，在操作的过程中有一些细节我们需要注意：

• 如果用于聚类的数据存在量纲上的差异，就必须对其做标准化处理
• 如果数据中含有离散型的字符变量，就需要对该变量做预处理，如设置为哑变量或转换成数值化的因子
• 对于未知聚类个数的数据集而言，不能随意地决定其簇数，而应该使用探索的方法寻找最佳的k值

小结

本篇介绍了无监督的聚类算法——Kmeans聚类，并详细讲述了理论知识，然后在两个数据集中进行了实践，特别是在对NBA球员数据集进行聚类之后，我们通过观察聚类的结果，可以对比球员的好坏，在实际应用中可以帮助我们进行人才的挑选。

虽然该聚类方法强大而灵活，但却存在明显的缺点。首先，该算法对于异常点十分敏感（一种解决的方法是先删除异常点，以防止其对聚类结果的影响），因为中心点是通过样本均值确定的，该算法不适合发现非球星的簇，因为它是基于距离的方式来判断样本之间的相似度（如果以某一个样本点为参照，假设距离其不超过某个值就认为是同一个簇中的样本，很明显用图形表示为以该样本点为圆心，在距离为半径的范围内都认为与其在同一个簇中）。

通过本篇对Kmeans的介绍及应用，我们可以应用到实际工作中来解决某些分类问题。

后记

本篇博文是笔者学习刘顺祥老师所著书籍《从零开始学Python数据分析与挖掘》后整理的部分笔记，文中引用了大量的原书内容，修正了书中部分错误代码，并加入了部分笔者自己的理解。

笔者在整理过程中，对书中作者提及但没有详细解释的概念尽可能地进行了解释，以及加入自己的理解，学习一个模型、明白如何构建模型以及用于预测过程比较简单，但是要理解模型背后的数学意义及原理是十分困难的，笔者尽可能地进行了介绍，但由于笔者才疏学浅，无法完全理解各个参数背后的数学原理及意义，还请有兴趣的读者自行上网查找相关资料。

• 参考自《从零开始学数据分析与挖掘》 [中]刘顺祥 著
• 完整代码及实践所用数据集等资料放置于：Github