《大话机器学习算法》贝叶斯—用贝叶斯计算吃火锅的概率

写在前面的话

前面用了三篇内容讲了决策树算法，也算是浅入浅出了，对于入门来说还是足够的

• 大话系列 | 决策树（上篇）—理论
• 大话系列 | 决策树（中篇）—理论
• 大话系列 | 决策树（下篇）—实战

学完之后，你应该已经掌握了：

决策树理论+算法优缺点+建立决策树+参数优化

如果你还没有掌握决策树的这些技能点，根据贝叶斯原理你有90%的概率也掌握不了这篇

假设你已经掌握了上面决策树的内容，那么学完这篇你会掌握以下技能：

• 一种新的分类算法（贝叶斯分类）
• 一个很有名气的概率计算公式
• 随时随地计算下一顿吃火锅的概率

准备好了吗？

情景一：一起吃个饭吧

在许媒婆的有意撮合之下，韩梅梅的第一个相亲对象竟然是老同学李雷雷

强忍住自己内心小九九的韩梅梅终于接到了李雷雷的邀请

李雷雷： 梅梅，明天有空吗？一起出去吃个饭？

李梅梅： （略一思考）刚好明天也没啥事，我们吃什么呢？

李雷雷： 好嘞，那我们就根据明天的天气决定吃什么吧

李梅梅： （吃什么要根据天气决定？不应该根据我的喜好？）

感觉到一丝异样的李雷雷连忙补充道：

李雷雷： 别急别急，你先听我说完

是这样的，从今年年初开始，一共有20天是下雨天，这20天里面有15天你是在家里吃饭，其中有9顿是在家打火锅，有5天是不在家吃饭，这5天有一天是去和朋友去外面吃火锅。

所以呢，如果明天下雨，根据历史数据，你可能最想吃火锅噢。

韩梅梅： （俏脸微红）你怎么会知道这个数据？许姨不是说不告诉外人嘛

李雷雷： （嘿嘿一笑）如果明天下雨了，在家吃火锅？

韩梅梅： 好啊好啊，你怎么会知道我这样想的？

李雷雷： 因为我会计算正向概率！

一共20天，其中15天在家吃饭，所以在家吃饭的概率：15/20=75%

而且啊，15天里面有9天在家吃火锅，在家吃火锅的概率：9/15=60%

另外啊，不在家吃火锅的概率：1/5=20%

韩梅梅： 厉害！不过你说的正向概率是什么？

上面的问题就是正向概率，表示从前往后推导一件事情发生的概率，你可能还听过一个词：先验概率，它两一回事

对了，还有一个是条件概率，例如 P(吃火锅|在家吃) 表示在家吃饭的时候吃火锅

相应的逆向概率就是从反向推理事物发生的概率，也叫后验概率

李雷雷： 给你出道题，如果明天吃火锅，那明天在家吃的概率是多少？算对了明天就去吃火锅！

韩梅梅： …（准备打人了）

哈哈哈哈，算不出来别生气，我们这里就用到了逆向概率。

贝叶斯原理

来，一起理一下思路：

我们知道，在家吃饭的概率 ：

$$P(在家吃)=15/20=75\%$$

在家吃火锅的概率：

$$P(在家吃火锅)=9/15=60\%$$

另外还有，不在家吃饭的概率 ：

$$P(不在家吃)=5/20=25\%$$

不在家吃火锅的概率 ：

$$P(不在家吃火锅)=1/5=20\%$$

这里，有两点需要注意一下：

• 在家吃火锅≠在家的时候吃火锅
• 不在家吃火锅≠不在家的时候吃火锅

因为后者是一个联合概率，表示（不）在家的条件下吃火锅

所以后者可以这样表示：

$$P(在家的时候吃火锅)=P(在家吃)\ast P(吃火锅|在家吃)$$

$$P(不在家的时候吃火锅)=P(不在家吃)\ast P(吃火锅|不在家吃)$$

那么我们可以算出来，下雨天吃火锅的概率：

$$P(吃火锅)=P(在家吃)\ast P(吃火锅|在家吃)+P(不在家吃)\ast P(吃火锅|不在家)=50\%$$
回到我们的问题，今天吃火锅的条件下，在家吃的概率是：

$$P(在家吃|吃火锅)=\frac{P(在家的时候吃火锅)}{P(吃火锅)}=\frac{P(在家吃)\ast P(吃火锅|在家吃)}{P(吃火锅)}=\frac{75\%\ast 60\%}{75\%\ast 60\%+25\%\ast 20\%}=90\%$$

韩梅梅： 好高啊，我有点怀疑这个数字

那我们也可以反向验证一下：

吃火锅一共10次，在家吃9次，不在家吃1次，所以在家吃的概率是90%

李雷雷： 算不出来没关系，我这有一个万能公式

韩梅梅： 快、快告诉我

我们直接另 吃火锅=B，在家吃=$A_1$，不在家吃=$A_2$，整理一下就是大名鼎鼎的贝叶斯公式：

$$P(A_1|B)=\frac{P(A_1)\ast P(B|A_1)}{P(A_1)\ast P(B|A_1)+P(A_2)\ast P(B|A_2)}$$
因为吃火锅只有两种情况，在家吃和在不在家吃，刚好对应了分母中的两种情况。

于是贝叶斯公式经常这样写：

$$P(A_1|B)=\frac{P(A_1)\ast P(B|A_1)}{P(B)}$$

似然函数

其实这里还有一个知识点，叫做似然函数，以及最大似然估计，我直接贴过来以前的文章，都有写过：贝叶斯的相关概念

以下是摘录：

似然却刚好与概率相反，是在已经确定的结果下推测产生这个结果的可能参数θ。注意，是已经确定了结果的前提下。

还是抛硬币的例子：
随机抛一枚硬币100次，结果出现60次数字朝上，那我们去判断这枚硬币的时候发现这并不是一枚标准的硬币，因为数字朝上的概率60%>人头朝上的概率40%。

我们运用出现的结果去判断事情本身的性质（参数），也就是似然。

情景二：吃什么我说了算！

朴素贝叶斯

韩梅梅： 我记得在学校里面老师还教过朴素贝叶斯，那又是什么？

之所以称为朴素贝叶斯，是因为它假设每个输入变量是独立的

就比如高富帅三个特征之间互不影响，帅的不一定高，高的不一定富

于是，求一个人高富帅的概率：

$$P(ABC)=P(A)\ast P(B)\ast P(C)$$
通过朴素贝叶斯预测概率的时候，只需要用数据训练一个贝叶斯模型，其实也就是计算出先验概率和条件概率，然后贝叶斯就可以预测出后验概率来。

就好比明天下雨了我们要不要吃火锅呢？在家吃还是去外面吃呢？都可以通过朴素贝叶斯算出概率

韩梅梅： 吃！我说了算！和贝叶斯无关

李雷雷： 好好好

你别看现在我们是用来做预测，其实贝叶斯最适合解决分类问题

举几个例子你就知道了：

垃圾邮件你应该有了解过，贝叶斯通过前期的系列训练，可以将未来的邮件进行分类(正常or垃圾)

世界杯比赛球队的输赢预测，通过历史球队战绩预测最终的输赢，也是通过贝叶斯实现的

在实际分类过程中，贝叶斯分类主要包括两种：离散数据的分类和连续数据的分类

离散数据的分类

离散数据的分类根据…

韩梅梅： 别急别急，你先告诉我什么是离散数据？

离散数据是有明确边界的数据，就像身高的高中低，成绩的排名1234等，像1~100之间的任何数组组成的数据集就是连续数据。

离散数据的分类是根据贝叶斯定理实现，特别是朴素贝叶斯的应用

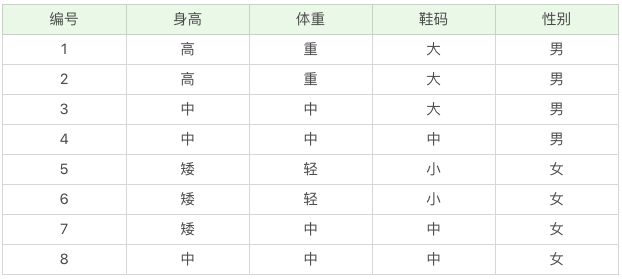
看个例子呗，如果说现在有一个人的特征是：身高中、体重中、鞋码大 ，这个人是男的还是女的？请你来分个类

ok，我们先确定一下属性：

$A_1$=身高中，$A_2$=体重中，$A_3$=鞋码小，$B_1$=男，$B_2$=女

我们的目的是计算$P(B_1|A_1{A}_2{A}_3)$和$P(B_2|A_1{A}_2{A}_3)$，对应概率大的就是结果了

前面已知贝叶斯公式：

$$P(B_1|A_1{A}_2{A}_3)=\frac{P(B_1)\ast P(A_1{A}_2{A}_3|B_1)}{P(A_1{A}_2{A}_3)}$$

$$P(B_2|A_1{A}_2{A}_3)=\frac{P(B_2)\ast P(A_1{A}_2{A}_3|B_2)}{P(A_1{A}_2{A}_3)}$$

分母都一样，那我们直接比较分子就行了

又根据朴素贝叶斯：

$$P(A_1{A}_2{A}_3|B_1)=P(A_1|B_1)\ast P(A2|B_1)\ast P(A_3|B_1)$$
直接计算：

$$P(B_1)\ast P(A_1{A}_2{A}_3|B_1)=\frac{1}{2}\ast \frac{1}{2}\ast \frac{1}{2}\ast \frac{0}{4}=0$$

$$P(B_2)\ast P(A_1{A}_2{A}_3|B_2)=\frac{1}{2}\ast \frac{1}{4}\ast \frac{1}{2}\ast \frac{1}{2}=\frac{1}{32}$$

第二个结果对应的是女孩子，那就是她了

连续数据的分类

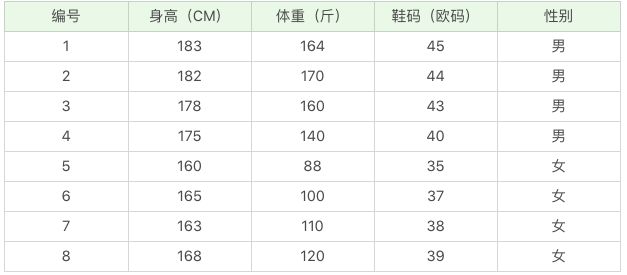
连续型数据的进行分类一般有两种方法，先看数据集：

一种方法是我们将连续型数据转换为离散型

比如说体重特征我们设置几个范围T1(100-120)，T2(120-140)…这样子连续型数据映射在相应范围，实现离散化

按照上面离散化的处理方式即可

另一种方式是我们假设身高、体重、鞋码都是正态分布，通过样本计算出均值和方差

还记得正态分布的密度函数吗，我们把点的值带进去，就能得到相应的概率值。

韩梅梅： 没看出来贝叶斯公式这么厉害！

李雷雷： 哈哈，那是，用处也挺大的呢。另外我已经预约好了座位，明天不见不散！

总结一下

理解贝叶斯算法之前先了解贝叶斯定理，也就是后验概率的计算；在此基础上，通过了解朴素贝叶斯的特性，对离散和连续数据进行分类操作。

相比而言，朴素贝叶斯简单很多，算法应用也很简单，下节通过项目我们一起实战一下贝叶斯分类。

贝叶斯算法的优缺点

优点：

• 对待预测样本进行预测，过程简单速度快

• 对于多分类问题同样有效，复杂度也并不会有大程度提升

• 在分布独立这个假设的情况下，贝叶斯分类器效果奇好

• 对于类别类的输入特征变量，效果奇好；对于连续型变量特征，默认符合正态分布

缺点：

• 测试集中的一个类别变量，训练集中没出现过，则概率为0，预测就没用了。
  可以使用平滑操作（拉普拉斯平滑）

• 朴素贝叶斯独立分布的假设，实际生活中很难完全独立

• 朴素贝叶斯不存在bagging、boosting等模型融合的方法（因为没有variance可以减少）

最后，请收下这个吧

思维导图会被后台二压，不介意的同学在原文链接中获取

原文链接： 大话系列 | 贝叶斯（上）—下雨天吃什么？

写在后面的话

贝叶斯分类主要是那几个公式，大家理解了就好，不算是特别难，所以我就直接贴公示出来了

千万不要一看见公式就自我放弃，稍微用点心思去看，你收获的肯定不止是一个算法。

我是小一，我们 下节见

文章首发：公众号【知秋小一】

文章同步：掘金，简书，csdn

欢迎三连支持小一，持续更新中

大话系列文章：

《大话机器学习算法》决策树—看这一篇就够了
《大话机器学习算法》决策树—实战项目之泰坦尼克生存预测