【数据极客】Week3_训练深度神经网络的技巧

Tips for Training DNN 训练深度神经网络技巧

【李宏毅2017秋天 课程】

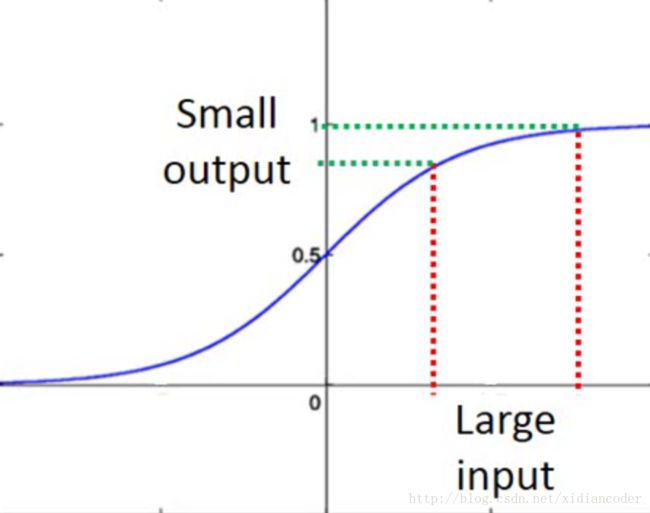
1 Vanishing Gradient Problem 梯度消失问题

在输入层部分，即便有很大的变化，通过 Sigmoid 激活函数之后， 输出结果都会被映射在0到1之间，对于输出层对损失函数的微分是比较小的，造成梯度消失问题。

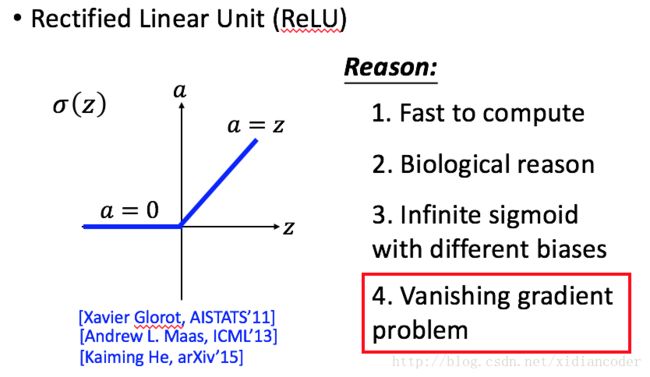
2 ReLU (Rectified Linear Unit)

• ReLU
  
  
  • 计算速度快
  • 生物学理由
  • 无穷多的带有不同偏置的 sigmoid 函数
  • 解决了梯度消失问题

如果某个 neuron 输出是0， 说明该节点是无用的， 可以直接从网络中去掉， 剩下的 非零 节点就是线性的。

结果函数是ReLU的话， 那么局部网络是线性的， 整体网络是非线性的。

• ReLU - variant
  

3 Maxout

选取每一组的最大的输出值作为最终的输出结果。放多少个元素为一组， 自己可以调参。

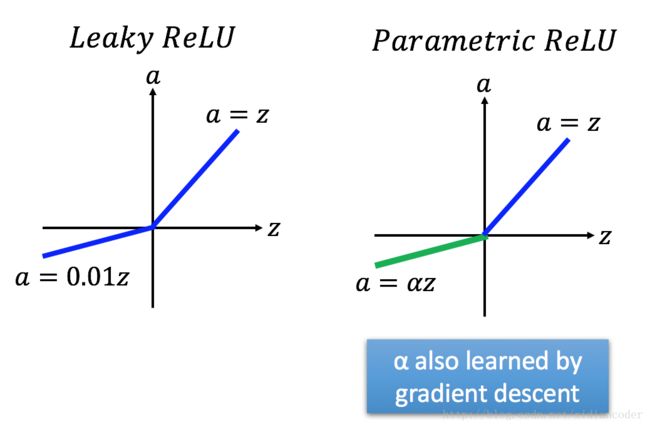
ReLU是一个特殊的Maxout， 但是Maxout相较于ReLU的优势在于，Maxout可以根据不同的参数学习出不同的激活函数(Activition Function)

右边绿色折线部分就是学习出来的激活函数。

4 Adaptive Learning Rate

Adagrad

具体可参照 1.2 节内容

在Adagrad的更新规则中，学习率 η 会随着每次迭代根据历史梯度的变化而变化。

ηt=ηt+1√

σt=1t+1∑ti=0‾‾‾‾‾‾‾‾‾√(gi)2

wt+1=wt−ηtσtgt

分子分布约分之后得到 wt+1=wt−η∑ti=0(gi)2√gt

∑ti=0(gi)2 代表前 t 步梯度平方的累加和。

这里分母可能为0， 所以在分母位置加上一个极小值 ϵ , 变为 wt+1=wt−η∑ti=0(gi)2+ϵ√gt

可以看到算法不断的迭， 分母会越来越大， 整体的学习率会越来越小。

#### RMSProp

RMSProp 是进阶版的 Adagrad

与Adagrad不同的是在分母位置， 累加之前几部的梯度平方和的时候， 进行了加权求和。

其中 a 参数是可以自己调节大小的。

5 Momentum 动量

其中 vi 是前 i 步的梯度加权求和：

∇(θ0) , ∇(θ1) , ∇(θ2) ,……, ∇(θi−1)

v0=0

v1=−η∇(θ0)

v2=−λη∇(θ0)−η∇(θ1)

…..

6 Adam

Adam = RMSProp + Momentum

7 Early Stopping 提早终止

需要验证集 Validation Set 确定 Testing Set 中的最小的损失函数值是多少。

8 Regularization 正则化

- New loss function to be minimized 新的最小化损失函数

找到一组权重， 不仅要最小化 Original Loss 的损失函数同时还要让接近0

L(θ) 为 Original Loss,可以是最小二乘法最小化损失函数、也可以是交叉熵损失函数。。。

L′=L(θ)+λ12∥θ∥2

右下角，是当损失函数为 L2 2范数的时候， 正则化项的形式， 通常在计算的时候不考虑正则化项。

η 是学习率，其数值很小， λ 通常也会设置为一个比较小的值。
所以 ηλ 这两个很小的数值相乘结果也非常小。

1−ηλ 的结果接近于 1 ， 比如： 0.99

每一个参数在update之前都会乘上一个接近于 1 的数， 这也就是所有的权值参数为什么越来越小的缘故， 权值衰减。

• 规则化项用 L1 范数的时候

L′=L(θ)+λ12∥θ∥1

sgn(w) 指的是：当 w>0 的时候， sgn(w)=1 ， 当 w<0 的时候 sgn(w)=−1 , 当 w=0 的时候， sgn(w)=0

对于 L1 范数来说， 每次通过减掉固定的值来是的参数值变小，而 L2 中每次乘以一个很小的数值， 来使得参数变小。

总结：

使用L1范数作为正则化项的时候， 得到的参数权重都较为接近，弱的特征对应的系数是0， 学到的模型稀疏的( w 经常为0)； L2范数作为正则化项的时候， 得到的参数权重都比较小， 取值变得平均， 表示能力强的特征对应的系数是非零的。

9 Dropout

当Testing Data表现不好的时候才使用，