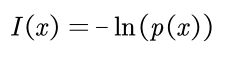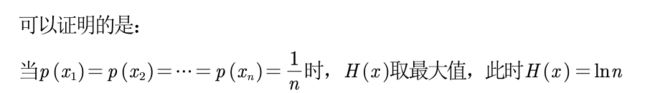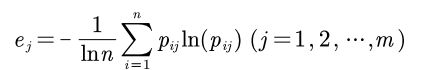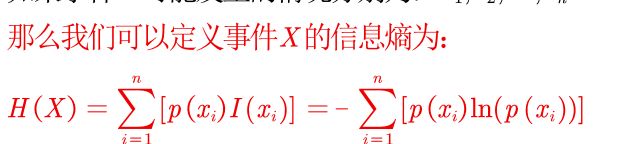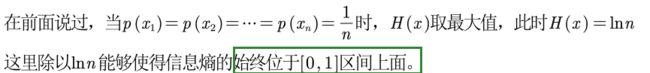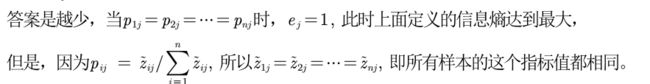基于熵权法对TOPSIS模型的修正

IMMC2020：熵权TOPSIS

笔记整理来自清风老师的数学建模课程：TOPSIS教程

目录

1. 熵权法的原理（客观赋权的方法）

2. 如何度量信息量的大小

 3. 信息熵的定义

 4. 熵权法的计算步骤

4.1 将输入矩阵中的负数变为正数（指标标准化）

4.2 计算概率

4.3  计算信息熵

5. 熵权法背后的原理

 6. 熵权法代码实现

7. 熵权TOPSIS代码实现

---

1. 熵权法的原理（客观赋权的方法）

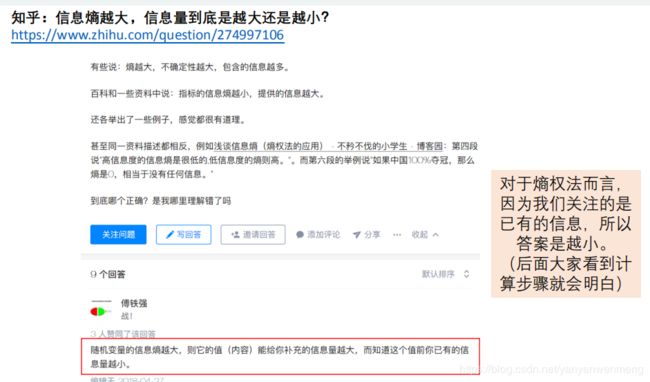
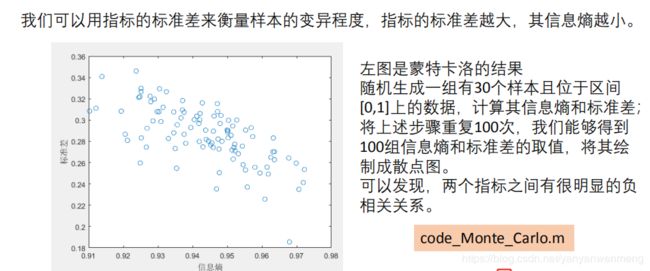
变异程度相当于方差或者标准差，权重低，表示的信息量比较小。

2. 如何度量信息量的大小

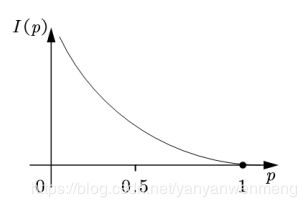
 如果把信息量用字母I表示，概率用p表示，那么我们可以将它们建立一个函数关系：

                                                                                        （图1） 

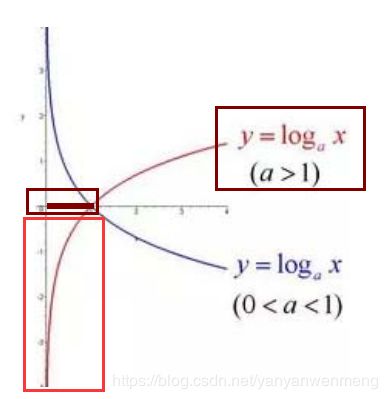
 可以发现概率越大，信息量越小。这种关系可以用log函数来表示：

                                                                                           （图2） 

X为【0,1】之间的数，ln的取e为底，相当于红框中的部分取个负号（y由负数变为正数）就得到了图1中的函数图像。

常量e约2.718282 对数函数介绍（视频）

因此可以得到：信息量与概率的函数关系式

 3. 信息熵的定义

 信息熵=概率与信息量乘积之和。

期望值的含义

n:事件发生的情况的总数

熵越大，信息量是越大还是越小呢？

 4. 熵权法的计算步骤

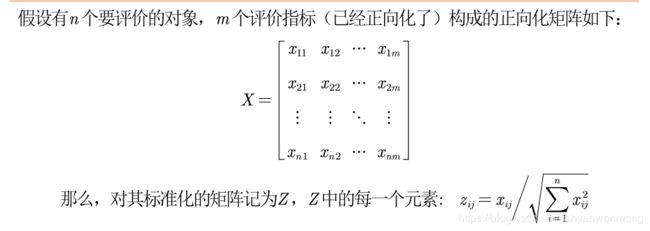
4.1 将输入矩阵中的负数变为正数（指标标准化）

判断输入的矩阵中是否存在负数，如果有则要重新标准化到非负区间 （后面计算概率时需要保证每一个元素为非负数）

 

一般用下面这种标准化的方法：

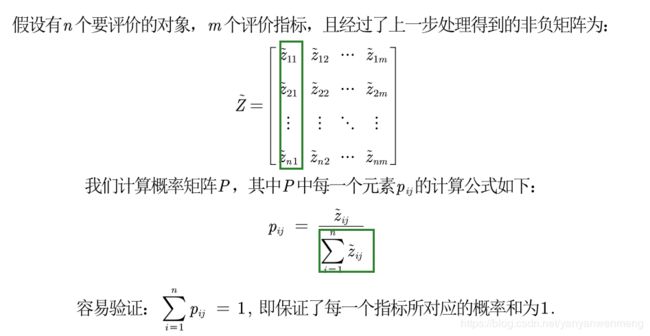
4.2 计算概率

 计算第j项指标下第i个样本所占的比重，并将其看作相对熵计算中用到的概率。 

概率计算有点像指标归一化。将每一个数除以这一列数之和。 

 

4.3  计算信息熵

计算每个指标的信息熵，并计算信息效用值，并归一化得到每个指标的熵权

 

对于第j个指标而言，其信息熵计算公式为：

相当于前面计算信息熵的公式除以了lnn

 （1）为什么这里要除以lnn这个常数

（2）为什么要将信息熵归一到[0,1]上面

其实是为了计算信息效用值

 

（3）熵权的计算

（4）一个指标的信息熵ej越大 ，那么这个指标代表的信息越少？为什么？

 所以这里引出了信息效用值，表示dj越大，表示的信息越多。

5. 熵权法背后的原理

 

 6. 熵权法代码实现

由于MATLAB中，ln（0）的结果返回不是0，所以需要重新定义一个log函数，说明一下这种特殊情况，使得ln（0）的返回结果为0

% 重新定义一个mylog函数，当输入的p中元素为0时，返回0
function [lnp] =  mylog(p)%lnp为输出变量，p为输入变量
n = length(p);   % 向量的长度
lnp = zeros(n,1);   % 初始化最后的结果
    for i = 1:n   % 开始循环
        if p(i) == 0   % 如果第i个元素为0
            lnp(i) = 0;  % 那么返回的第i个结果也为0
        else
            lnp(i) = log(p(i));  
        end
    end
end

熵权法的代码：

function [W] = Entropy_Method(Z)
% 计算有n个样本，m个指标的样本所对应的的熵权
% 输入
% Z ： n*m的矩阵（要经过正向化和标准化处理，且元素中不存在负数）
% 输出
% W：熵权，m*1的行向量

%% 计算熵权
    [n,m] = size(Z);
    D = zeros(1,m);  % 初始化保存信息效用值的行向量
    for i = 1:m
        x = Z(:,i);  % 取出第i列的指标
        p = x / sum(x);
        % 注意，p有可能为0，此时计算ln(p)*p时，Matlab会返回NaN，所以这里我们自己定义一个函数
        e = -sum(p .* mylog(p)) / log(n); % 计算信息熵
        D(i) = 1- e; % 计算信息效用值
    end
    W = D ./ sum(D);  % 将信息效用值归一化，得到权重    
end

7. 熵权TOPSIS代码实现

D_P = sum([(Z - repmat(max(Z),n,1)) .^ 2 ] .* repmat(weight,n,1) ,2) .^ 0.5;   % D+ 与最大值的距离向量
D_N = sum([(Z - repmat(min(Z),n,1)) .^ 2 ] .* repmat(weight,n,1) ,2) .^ 0.5;   % D- 与最小值的距离向量
S = D_N ./ (D_P+D_N);    % 未归一化的得分
disp('最后的得分为：')
stand_S = S / sum(S)

TOPSIS代码实现（不加权重）