transformer详解：transformer/ universal transformer/ transformer-XL

特别鸣谢刘陆琛@Mayouji在本文写作过程中的帮助

Attention机制在NLP领域的应用最早可以追朔到2014年，Bengio团队将Attention引入NMT(神经机器翻译)任务 [1]。之后更是在深度学习的各个领域得到了广泛应用：如CV中用于捕捉图像上的感受野；NLP中定位关键token/feature.

作为某种程度上可以称为当下NLP领域最强的特征抽取器的transformer [2]，同样不是一蹴而就的：

• Transformer
  首个完全抛弃RNN的recurrence，CNN的convolution，仅用attention来做特征抽取的模型
• Universal Transformer
  重新将recurrence引入transformer，并加入自适应的思想，使得transformer图灵完备，并有着更好的泛化性和计算效率
• Transformer-XL
  在transformer的基础上加入Segment-level Recurrence和相对位置编码，从而可以处理超长输入序列，并且更加高效。

在文章开始，首先尝试提出几个问题，来帮助我们理解transformer这一系列模型的思想：

1. 为什么要引入attention机制？
   Attention机制理论上可以建模任意长度的长距离依赖，并且符合人类直觉
2. transformer有哪些优点和不足？
   完全基于attention，在可以并行的情况下仍然有很强的特征抽取能力，缺点是仍然是自回归的形式、理论上非图灵完备、缺少Recurrent Inductive Bias和条件计算、对超长序列建模能力较差
3. universal transformer相较于transformer做了哪些改进，有什么不足？
   利用Recurrence将transformer的层数由6改为了任意层，并且理论上实现了图灵完备（指的是计算上通用）；加入自适应计算的思想，使得模型计算更加高效。
4. transformer-XL的特点，优势是什么？
   引入Segment-level Recurrence，使得transformer可以解决“上下文碎片问题”并捕捉更长距离的依赖，从而可以处理超输入序列

transformer仍然是基于seq2seq，所以介绍attention机制之前，需要先介绍下“前attention”时代，NLP领域中的seq2seq。

seq2seq简介

文中关于seq2seq的介绍均以机器翻译应用为例。

RNN-based seq2seq

seq2seq最早来源于通信，对应过程中的编码和解码。在NLP领域中，seq2seq主要用来解决将一个序列X转化为另一个序列Y这一类问题，通常应用于机器翻译、自动摘要等端到端的生成式应用。seq2seq有一个很重要的特点：输入序列X和输出序列Y可以不等长，不需要一一对应。

传统的seq2seq是条件语言模型，即在已知输入序列X和生成序列Y中已生成词的条件下, 最大化下一目标词的概率，而最终希望得到的是整个输出序列的生成出现的概率最大：
$$P(Y|X)=\sum _{t=1}^T\log P\left(y_t|y_{1:t-1},X\right)$$
其中：

• X为输入序列
• T代表时刻，$y_{1:t-1}$则代表decoder前t-1时间的输出

1. 对于seq2seq而言，在训练时$y_{1:t-1}$是ground truth tokens；而在测试的时候，没有ground truth tokens，此时是采用decoder生成的$y_{1:t-1}^{\prime }$来预测下一个词。训练和预测时这种不一致，也是seq2seq中长期存在的“暴露偏差”的根源，针对这一问题，也有很多的工作，这里就不再展开。
2. 上述过程预测输出序列Y的token时，是根据之前时刻的结果$y_{1:t-1}^{\prime }$来预测下一个token，即极大化下一目标token的概率，这是一种典型的贪心策略，得到的是局部最优；而对于一般的端到端生成模型而言，希望得到整个序列的最佳，即最后的生成序列Y的tokens顺序排列的联合概率最大，找到一个全局最优。实际过程中seq2seq在预测时并不使用这种greedy search的策略，而是采用beam search。不过本文主要讲述transformer，seq2seq仅做一个便于问题理解的概述。

下图是一个基本的RNN-based seq2seq（图中的箭头可以描述信息传导过程）：

Encoder会将输入序列X编码为一个固定长度的语义向量C：在编码过程中，时刻t的输出仅依赖前一时刻隐层$h_{t-1}$ 和当前时刻的输入$x_t$
Decoder的输入是encoder得到的语义向量$C$：解码过程中，时刻t的输出依赖于三个部分，上一个时刻隐层状态$h_{t-1}$和中间语义向量$C$和上一个时刻的预测输出$y_{t-1}$
Seq2Seq两个部分(Encoder和Decoder)联合训练的目标函数是最大化条件似然函数：
$$\underset{\mathbf{\theta }}{\max }\frac{1}{N}\sum _{n=1}^N\log p_{\mathbf{\theta }}\left({\mathbf{y}}_n|{\mathbf{x}}_n\right)$$
其中θ为模型的参数，N为训练集的样本个数。

seq2seq中encoder的输入$x_i$和decoder中的输出$y_i$都是词的高维向量表示，向量中蕴涵一定的语义信息，之所以可以用一个高维向量来表示词的语义，其基本假设是上世纪语言学家提出的分布式语义的思想：其认为一个词可以由上下文中的词来表示。

有了分布式语义，我们就可以来理解NLP问题中普遍存在的长距离依赖，考虑语言模型中依据之前的词来预测下一个词：

• 如果我们试图预测“the clouds are in the sky”中的最后一个单词，我们不需要任何更多的上下文信息，从"clonds", “in” 这些近距离的词就可以预测到下一个单词是“sky”
• 而如果尝试预测“I grew up in France… … I speak fluent French.”中的"French"，那么需要重点关注远距离的"France"。

上述例子可以表明，当我们做预测时，可能需要重点关注的信息与当前位置的距离非常大，RNN很难保留这种远距离的信息。这就是NLP中普遍存在的长距离依赖。即使有如LSTM，GRU这样加入门控机制和梯度裁剪的RNN变种，其捕捉长距离依赖的能力仍然有所欠缺，Stanford在ACL 2018的一个工作[5]进行了实验，目前可以编码的最长距离在200左右。

RNN-based seq2seq with attention

RNN在将一个不定长输入序列转化为定长的中间语义向量时，会有信息损失，为了避免这样的损失，就引入了Attention机制。Attention机制本身有些类似于人类的直观活动：人在观察一副图画时，直觉会重点关注“更为重要”的信息；人类译者在做翻译时，也会更侧重当前翻译部分所对应的上下文。基于这样的原理，Attention机制在做机器翻译时，会尝试关注源语句中“更为重要”信息，再结合已经翻译的部分，最终得出当前译文。

下面的动图可以很好的描述一个基本的RNN-based seq2seq信息传导过程（图片来源于google seq2seq示例 [4]），在解码得到“Knowledge”时，会将注意力集中在源语句中的“知识”。

结合了attention的seq2seq，不再局限于定长的语义向量，理论上也不会损失远距离的信息，在实际应用过程中也取得了很好的效果。既然如此，一个朴素的想法就是“既然attention机制已经很有效，那么我们去掉RNN，直接用attention的效果会怎么样？” Google在2017年提出的transformer就是一个完全基于self-attention的seq2seq模型。

Transformer

下面的动图（来自于Google AI Blog[6]）演示了transformer在机器翻译中的应用：

• Encoder：读取输入语句并生成其representation。
• Decoder：参考Encoder生成的输入语句的representation，逐词生成输出语句。

transformer首先为每个单词生成初始表示或使用预先定义的wordembedding，动图中用空白的圆表示；然后通过self attention，从所有其他单词中收集信息，生成一个新的representation，每个单词由整个上下文(动图中由填满的圆表示)的信息来表示。然后，对所有单词并行重复此步骤多次，依次生成新的representation。

下图（左）是transformer的一个基本架构，左边是编码的部分（transformer的Encoder由6个这样相同的层堆叠而成），右边是解码的部分（transformer的Decoder由6个这样相同的层堆叠而成），下图（右）是展开的示意图

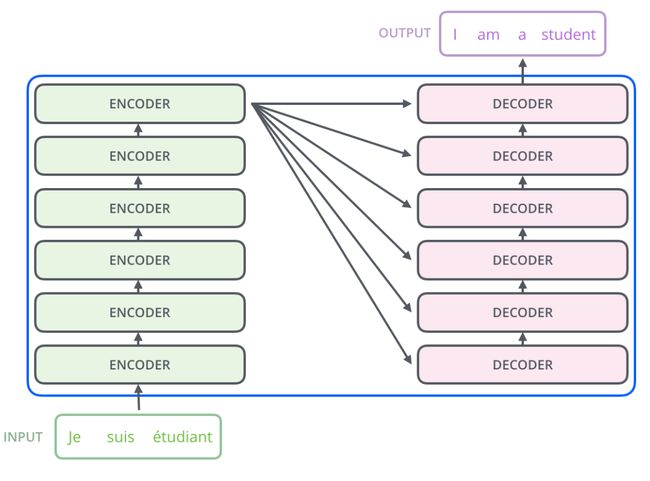Encoder：由6个相同的层堆叠而成，每层有两个sub layer：multi-head self-attention层和一个全连接前馈神经网络；sub layer之间经layer normalization后，再通过residual connection连接。
Decoder：整体类似于Encoder，多了一层multi-head self-attention，用于在encoder stack的输出上加入multi head attention；在multi-head self-attention层中假加入masking，从而确保了位置i的预测只能依赖于位置i之前的已知输出。（因为解码的时候，位置i之后的输入，并不存在，这样可以保持自回归的特性）

以上是对transformer的一个简要概述，以下将对transformer各个部分进行详解。

Attention

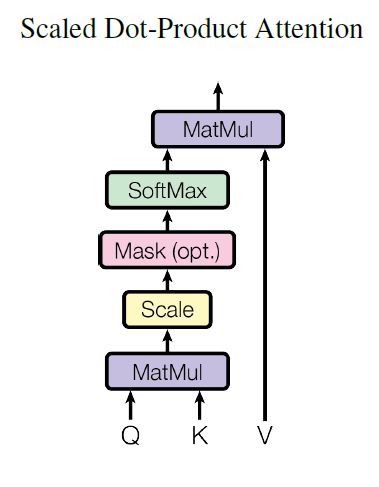
Scaled Dot-Product Attention

Self Attention本质上是将上下文词的representation加权求和作为当前词的representation。需要关注的部分是我们如何得到加权求和的权值。在Transformer中，这一部分用$Attention(Q,K,V)$来体现 ，Q是query，K是Key；通过Q和K的点积的结果来体现上下文词对当前词的影响程度，再通过softmax得到归一化权重：
$$\text{ Attention }(Q,K,V)=\mathrm{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$
在transformer中，每个单词会有一个语义向量，乘以权重矩阵$W_i^Q$,$W_i^K$,$W_i^V$，从而得到对应的$Q_i$,$V_i$,$K_i$.

$\sqrt{d_k}$是一个缩放因子，$d_k$是向量$Q_i$,$V_i$,$K_i$的维度，因为$Q_i{K}_i^T\in (0,d_k)$，当$d_k$比较大时，$Q_i{K}_i^T$值可能会很大，softmax之后可能会出现较多的值接近0。下图是Scaled Dot-Product Attention的示意图：

常用的attention主要有“Add-加”和“Mul-乘”两种（不清楚的可以参考[13])，文章中对于采用mul这种形式的解释是：两种方式的计算复杂度类似，然而mul可以采用矩阵乘法来加速。

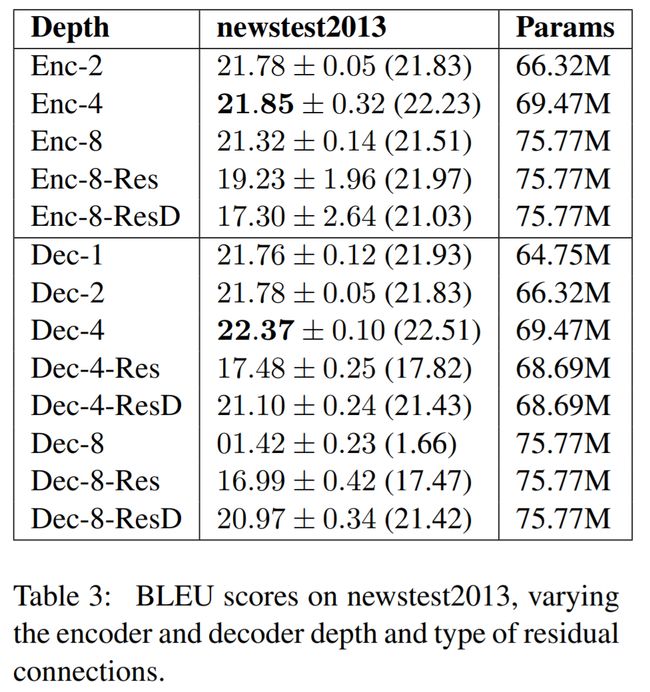
除了计算效率之外，在google的另一篇文章中[14]在newstest2013数据集上对两种attention进行了实验，有如下结果：

可以看出，当$d_k$增大时，mul attention的结果会更好。

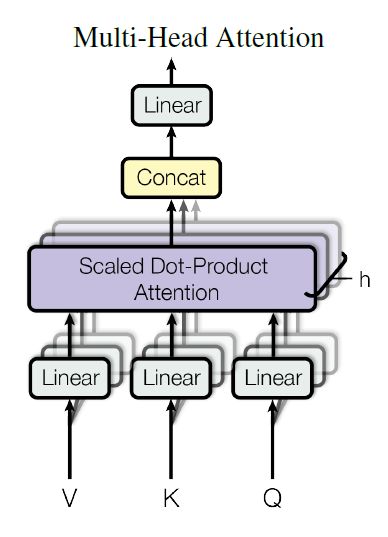
multi-head attention

transformer所用的attention并非上述那么简单，其会将原始512维$(Q,K,V)$通过8次不同的线性投影，得到8组低维的$(Q_i,K_i,V_i)$（64维），共投影8次；利用投影后的结果并行地进行8次线性投影，从而得到8个64维的输出，再拼接到一起得到multi-head attention的输出。示意图如下：

计算过程如下：
$$\begin{array}{rl}\text{ MultiHead }(Q,K,V)& =\text{ Concat }\left({\text{ head }}_1,\dots ,{\text{ head }}_{\mathrm{h}}\right)W^O\\ {\text{ where head }}_{\mathrm{i}}& =\text{ Attention }\left(Q{W}_i^Q,K{W}_i^K,V{W}_i^V\right)\end{array}$$

其中的投影参数矩阵$
{W_{i}^{Q} \in \mathbb{R}^{512\times 64}, W_{i}^{K} \in \mathbb{R}^{512\times 64}, W_{i}^{V} \in \mathbb{R}^{512\times 64}} $都是由模型学习得到

这样做的好处是：

• 可以综合各个单词，在不同表示子空间的信息
• 因为对单个attention layer而言，维度是变小了的，综合来看，multi-head attention和single-head attention的效率是一样的。

attention in transformer

在transformer中，共有3个部分使用了multi-head attention，下图中红框部分：Attention in Encoder-Decoder，Attention in Encoder和Attention in Decoder。

其中比较特殊的是Attention in Decoder，因为在解码的时候，仅知道当前词左边的部分。由此，利用masking（当前词右侧的内容被设置为−∞，这样softmax的值为0）屏蔽了当前词右边部分的影响，保持了自回归的特性。

Position-wise Feed-Forward Networks

decoder和encoder中都存在一个相同的全连接前馈神经网络，该网络包括两次线性变换，两次变换中间是一个ReLU激活函数
$$\mathrm{FFN}(x)=\max \left(0,x{W}_1+b_1\right)W_2+b_2$$
该网络有两个特点：

• 各个层中的网络结构相同，但是参数不同
• 输入和输出的向量维度均为512，中间层的维度是2048

论文在3.3小节对“Position-wise”进行了解释：“…which is applied to each position separately and identically…” 。即输入序列不同位置token在multi-head attention之后的结果，在FNN的过程中是不会相互影响的。

在multi-head attention结束之后，FNN层的输入矩阵$X\in R^{d_{input}\times d_{model}}$，输入序列中，不同位置token在attention之后的结果在不同行。这些结果会被映射到更高维的特征空间，经过Relu做非线性筛选，然后再恢复到原始维度，过程中$W_1\in R^{d_{input}\times d_{ff}},W_2\in R^{d_{ff}\times d_{model}}$. ($d_{ff}=2048,d_{model}=512$)

Embeddings and Softmax

这一部分和基础的seq2seq model类似，其中input embedding layer、output embedding layer 和pre-softmaxlinear transformation 共享权重。（在embedding layers 的会被乘上$\sqrt{d_{model}}$）

Positional Encoding

在NLP中，token的位置也是很重要的信息，例如“我喜欢林允儿”和“林允儿喜欢我”都由相同的token组成，然而意思则是天差地别。RNN-based的seq2seq由于recurrence的存在，已经编码了位置信息，attention机制则做不到这一点，为此，transformer中加入了位置函数来编码位置信息：
$$\begin{array}{rl}P{E}_{(pos,2i)}& =\sin \left(\mathrm{pos}/10000^{2i/d_{\text{model }}}\right)\\ P{E}_{(\text{pos, }2i+1)}& =\cos \left(\text{ pos }/10000^{2i/d_{\text{model }}}\right)\end{array}$$
其中pos是指当前词在句子中的位置，i是指向量中每个值的index：在偶数位置，使用正弦编码，在奇数位置，使用余弦编码。

之所以选用上述公式，是因为其能很好的编码相对位置，位置为pos+k的词可以由位置为pos和k的词来表示：
$$\begin{array}{c}PE(pos+k,2i)=PE(pos,2i)PE(k,2i+1)+PE(pos,2i+1)PE(k,2i)\\ PE(pos+k,2i+1)=PE(pos,2i+1)PE(k,2i+1)-PE(pos,2i)PE(k,2i)\end{array}$$
同时可以证明：间隔为k的任意两个位置编码的欧式空间距离是恒等的，只与k有关。

另一种编码位置的方式是学习position embedding (参考文献)；不过两种方法的效果类似，利用公式计算则更为简单，并且可以处理比训练时更长的序列。

Add & Norm

Add是残差连接，可以有效的改善深层模型中梯度消失的问题，且能打破网络对称性，从而减轻网络退化问题[17]

bag of tricks

transformer中还有一些细节，碎碎念：Transformer的细枝末节这篇文章已经写得很棒，就不再赘述。

• Weight Tying
• Learning rate warm-up
• Regularization
• Masking

缺陷

transformer一经提出，在NLP领域也引起了广泛关注，在当下（2019年）仍有很多任务的STOA方法是基于transformer的。当然transformer也存在着不足：

• 缺少Recurrent Inductive Bias：
  学习算法中Inductive Bias可以用来预测从未遇到的输入的输出（参考[10])。对于很多序列建模任务（如需要对输入的层次结构进行建模时，或者在训练和推理期间输入长度的分布不同时），Recurrent Inductive Bias至关重要。EMNLP 2018 上的一个工作[9]对这一点进行了实证。
• Transformer是非图灵完备的：
  非图灵完备通俗的理解，就是无法解决所有的问题（可以参考[12])
  在Transformer中，单层中sequential operation (context two symbols需要的操作数)是$O(1)$ time，独立于输入序列的长度。那么总的sequenctial operation仅由层数$T$决定。这意味着transformer不能在计算上通用，即无法处理某些输入。如：输入是一个需要对每个输入元素进行顺序处理的函数，在这种情况下，对于任意给定的深度$T$的transformer，都可以构造一个长度为$N>T$的输入序列，该序列不能被transformer正确处理
• transformer缺少conditional computation：
  transformer在encoder的过程中，所有输入元素都有相同的计算量，比如对于“I arrived at the bank after crossing the river", 和"river"相比，需要更多的背景知识来推断单词"bank"的含义，然而transformer在编码这个句子的时候，无条件对于每个单词应用相同的计算量，这样的过程显然是低效的。
• 不能很好的处理超长输入：
  理论上来说，attention可以关联两个任意远距离的词，但实际中，由于计算资源有限，仍然会限制输入序列的长度，超过这个长度的序列会被截断。

为了解决前三个问题，google在ICLR 2019上提出了transformer的改进版本universal transformer。

Universal Transformer

在transformer中，block的层数是固定的（base是6层），universal transformer则通过递归函数使得层数不再固定，可以是任意，下图是universal transformer encoder的示意图，横坐标position是输入序列token的位置；纵坐标是迭代次数depth。

上述模式综合了transformer的优点，同时又具备RNN的Recurrent Inductive Bias，并且在理论上做到了图灵完备。

universal transformer第二个比较大的改进是加入了dynamic halting: 基于自适应时间算法(Adaptive Computation Time, ACT) [11]，该算法由DeepMind在2016年提出。有了dynamic halting，在编码“I arrived at the bank after crossing the river", 对于"river"编码的递归次数会变少；对于“bank”的编码递归次数会相应更多.

下图是Universal Transformer with dynamic halting在encoder的一个示意图[7]，可以看到输入序列中，不同token的计算量不再相同，这样就实现了条件计算：

transformer-XL

在理解一篇文章时，为了理解当前一个词或者是句子，经常会出现需要参考上千个单词之后的词的请况，这种长距离距离很难捕获：理论上，基于attention机制可以让transformer捕获任意长度的依赖，然而由于资源有限， Transformer 通常会将语料分割为几百个字符的固定长度的片段，每个片段（segment）之间相互独立，独立处理

这样的方式存在两个问题：

• 能建模的依赖关系不会超过segment的长度
• 会导致context fragmentation（上下文碎片化）：因为分片并不是根据语义边界，而是根据长度划分，很有可能会将一个完整的句子分割，那么在预测一个segment的前几个token的时候，很可能缺乏必要的语义信息。

在transformer-XL中，采用Segment-level Recurrence来解决这个问题

Segment-level Recurrence

transformer-XL在文章中所对比的Vanilla Transformer model，也是google在AAAI 2019[18]上的一篇工作，其将transformer用于character-level的语言模型中：添加了多个loss来提高其表现并加快拟合速度；增大transformer层数来提高表现，最多到了64层。

下图是Vanilla transformer在训练时的示意图（segment长度为4）[19]：

在transformer-XL中，上一个时刻的segment的representation会被保存下来，并作为下一个segment的扩展上下文，整个过程类似于RNN。由此，可以捕获的最大依赖项长度增加了N倍（N是网络深度）；同时Recurrence使得编码当前segment时，仍然可以利用之前segment的信息，从而解决了context fragmentation问题。下图是transformer-XL在训练时的示意图（segment长度为4）：

Relative Positional Encodeing

如果只有Segment-level Recurrence，那么位置编码将会出现问题：因为每个segment中的位置编码是一样的，当重用之前segment的representation时，位置编码没有被区分，显然会出现问题，下述是transformer对于segment的处理，$h_{\tau }$代表对于第$\tau$个segment，transformer的输出；$E_{{\mathbf{s}}_{\tau +1}}$是第 $\tau +1$个segment的初始embedding；$U_{1:L}$代表位置编码。
$$\begin{array}{rl}{\mathbf{h}}_{\tau +1}& =f\left({\mathbf{h}}_{\tau },{\mathbf{E}}_{{\mathbf{s}}_{\tau +1}}+{\mathbf{U}}_{1:L}\right)\\ {\mathbf{h}}_{\tau }& =f\left({\mathbf{h}}_{\tau -1},{\mathbf{E}}_{{\mathbf{s}}_{\tau }}+{\mathbf{U}}_{1:L}\right)\end{array}$$

从上述式子中可以看出，对于任意一个segment，其位置编码都是相同的。

一个直观的解决方案是：将相对位置信息编码到扩展上下文中，其本质是捕获recurrence过程中的时序信息或者是偏差（temporal clue or “bias” ）。transformer-XL并没有采用将bias到扩展上下文的方案，而是使用相对位置编码：因为一个token在整个序列中的绝对位置并不重要，只需要在计算attention sorce时知道两个单词的相对位置即可。

transformer-XL的相对位置编码来源于对[20]和[21]的改进：这两个工作均来源于google，分别发表在了NAACL和ICLR，其将bias整合到了attention中：
$$\begin{array}{rl}{\mathbf{A}}_{i,j}^{\mathrm{a}\mathrm{b}\mathrm{s}}& =\underset{(a)}{{\mathbf{E}}_{x_i}^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_k{\mathbf{E}}_{x_j}}+\underset{(b)}{{\mathbf{E}}_{x_i}^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_k{\mathbf{U}}_j}\\ & +\underset{(c)}{{\mathbf{U}}_i^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_k{\mathbf{E}}_{x_j}}+\underset{(d)}{{\mathbf{U}}_i^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_k{\mathbf{U}}_j}\end{array}$$

$W_q{E}_{x_i}$得到的是第i个token的Query向量，$W_k{E}_{x_j}$得到的是第j个token的key向量，$U_i$代表第i个token的位置编码，所以：

• a是query向量和key向量的相乘
• b是query向量和key对应的位置编码相乘
• c是query对应位置编码和key向量相乘
• d是query对应位置编码和key对应位置编码相乘

实际上，上式是一个乘法分配律的展开式，而在transformer-XL中，做了三处改变：
$$\begin{array}{rl}{\mathbf{A}}_{i,j}^{\mathrm{r}\mathrm{e}\mathrm{l}}& =\underset{(a)}{{\mathbf{E}}_{x_i}^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_{k,E}{\mathbf{E}}_{x_j}}+\underset{(b)}{{\mathbf{E}}_{x_i}^{\top }{\mathbf{W}}_q^{\top }{\mathbf{W}}_{k,R}{\mathbf{R}}_{i-j}}\\ & +\underset{(c)}{u^{\top }{\mathbf{W}}_{k,E}{\mathbf{E}}_{x_j}}+\underset{(d)}{v^{\top }{\mathbf{W}}_{k,R}{\mathbf{R}}_{i-j}}\end{array}$$

• b和d中将Key的绝对位置编码$U_j$改为了相对位置编码$R_{i-j}$
  $R_{i-j}$是一个无需学习的sinusoidal编码矩阵，计算方式同最初的transformer。该方式可以避免不同segments之间由于tokens在各自segment的index相同而产生的时序冲突的问题。
• c和d中，将query的绝对位置编码进行了替换
  因为query相对于自己的位置是一样，a那么ttention bias的计算与query在序列中的绝对位置无关，应当保持不变
• $W_k$->$W_{k,E},W_{k,R}$
  在之前transformer中，token的embedding和position embedding会加起来，再经过$W_k$矩阵做线性变换，即embedding和position encoing是相同的线性变换，该处改变使得key的embedding和positional encoding 分别采用了不同的线性变换。其中$W_{k,E}$对应于key的embedding线性映射矩阵，$W_{k,R}$对应与key的positional encoding的线性映射矩阵

这样做的好处：

• 解决了在应用了Segment-level Recurrence之后，segment间位置编码冲突的问题
• 可以利用sinusoid 的inductive bias
  sinusoid并不会受限于序列长度，即使是训练时从未遇到的序列长度仍能很好的处理，这也一定程度上体现了inductive bias[10]

Faster Evaluation

Vanilla transformer在评估时，每个segment只会向前移动一个token的位置，这样的速度很慢：

而在transformer-XL中，是segment->segment的移动，更加高效

Results

• Transformer-XL学习的依赖项比RNNs长80%左右，比最初的transformer长450%，最初的transformer通常比RNNs具有更好的性能，但由于上下文的长度固定，不是远程依赖项建模的最佳选择
• 在评估语言建模任务时，ransformer-XL的速度比vanilla transformer快1800多倍，因为不需要重新计算（见Faster Evaluation部分）
• 由于有更好长距离依赖建模，Transformer-XL在长序列上具有更好的perplexity性能(更准确地预测样本)；而且通过解决上下文碎片问题，它在短序列上也有更好的性能。

Reference

1. Neural Machine Translation by Jointly Learning to Align and Translate
2. 放弃幻想，全面拥抱Transformer：自然语言处理三大特征抽取器（CNN/RNN/TF）比较
3. The Illustrated Transformer
4. Overview - seq2seq TF seq2seq文档
5. Sharp Nearby, Fuzzy Far Away: How Neural Language Models Use Context
6. Transformer: A Novel Neural Network Architecture for Language Understanding
7. Universal Transformers
8. Convolutional Sequence to Sequence Learning
9. The Importance of Being Recurrent for Modeling Hierarchical Structure
10. 如何理解Inductive bias？
11. Adaptive Computation Time for Recurrent Neural Networks
12. 什么是图灵完备？ - RanC的回答 - 知乎
13. 模型汇总24 - 深度学习中Attention Mechanism详细介绍：原理、分类及应用
14. Massive Exploration of Neural Machine Translation Architectures
15. 碎碎念：Transformer的细枝末节
16. Transform详解(超详细) Attention is all you need论文
17. 【模型解读】resnet中的残差连接，你确定真的看懂了？
18. Character-Level Language Modeling with Deeper Self-Attention
19. Transformer-XL: Unleashing the Potential of Attention Models
20. Self-Attention with Relative Position Representations
21. MUSIC TRANSFORMER: GENERATING MUSIC WITH LONG-TERM STRUCTURE
22. [NLP] 相对位置编码(二) Relative Positional Encodings - Transformer-XL