POJ 3494 Largest Submatrix of All 1’s 单调栈应用 图解+代码详解

传送门：POJ 3494

题目大意：求仅由0，1组成的矩阵中，全部由1组成的子矩阵的最大面积。

Sample Input

2 2
0 0
0 0
4 4
0 0 0 0
0 1 1 0
0 1 1 0
0 0 0 0

Sample Output

0
4

前置技能：1.单调栈原理及应用。

                  2.POJ 2559 题解。

思路：这个题本质上是POJ 2559的升级版，该题通过一定的预处理可以转换为POJ 2559，不得不说这种解法真是太奇妙了。下面给出我的思路以及我亲手所画的图解。

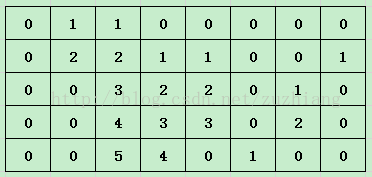
例如给出一个5X8的矩阵，如下图所示：

现在我们将其预处理一下，为了叙述的方便，我们规定最上方的行为第0行，最左边的列为第0列。如果第 i 行第 j 列的数为1，则它便等于第 i-1 行第 j 列的数+1；否则为0。通俗的来说，就是把每一列中连续的1从上到下的按升序给编号。得到下图：

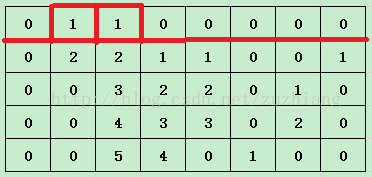
这样一来，可能你还没有发现有什么规律，没关系，慢慢来，随着我的思路来看。我们可以再处理一下，以每行的行底为底，以该底为底的矩形的高度就是这一行的数的值。比如下图中，矩形的高度分别为1，1。

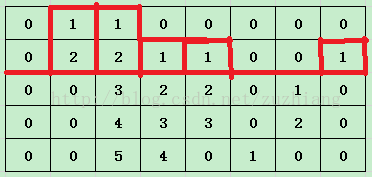
以第1行行底为底的矩形的高度如下图所示，为2，2，1，1，1.

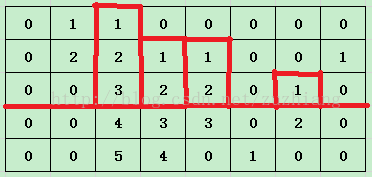
以第2行行底为底的矩形的高度如下图所示，为3，2，2，1。注意第1列，也就是值从上到下为1，2，0的一列，因为这一列在第2行的值为0，所以不能形成矩形。

好了，说到这估计大家都已经找到规律了，我就不再上图片了。这样以来是不是就转换成了先预处理一下，然后扫描每一行，求这一行中可以形成的矩形的最大面积，然后取个最大值即可。

具体实现：首先预处理一下，如果当前行为1，则当前行的值就等于上一行的值+1，否则为0。然后每一行用一个单调递减的单调栈处理，如果栈为空或入栈元素大于等于栈顶元素则入栈；如果栈非空并且栈顶元素小于入栈元素，则将栈顶元素出栈并更新面积最大值，直至栈为空或碰到第一个大于等于入栈元素的元素。然后将最后一次出栈的栈顶元素向左向右延伸，改变他对应的数组的值，并入栈。

为了最后让栈内所有元素都出栈，我们设数组最后一个元素的值为最小值。

注意：

1.单调栈保存的是每个矩形的位置。

2.在维护单调栈的过程中，也就是让最后一次出栈的栈顶元素向左向右延伸的时候，原数组中的值已经改变了。

3.由于会改变原数组，我又开辟了一个数组保存原来的值，以方便预处理。

4.最后一次出栈的栈顶元素就是当前入栈元素可以向左拓展到的最大距离。

#include
#include
#include
#include
using namespace std;

int main()
{
	//top指向栈顶；tmp为临时变量，记录面积的值；ans为答案，记录面积的最大值 
	int i,j,m,n,x,top,tmp,ans,h[2020],a[2020];
	stack st; //单调栈，记录位置 
	while(~scanf("%d%d",&m,&n))
	{
		ans=0;
		memset(h,0,sizeof(h)); //用于第一行的处理
		for(i=0;i=a[st.top()])
				{ //如果栈为空或入栈元素大于等于栈顶元素，则入栈 
					st.push(j);
				}
				else
				{
					while(!st.empty()&&a[j]ans) ans=tmp; //更新面积最大值 
					}
					st.push(top); //将最后一次出栈的栈顶元素延伸并入栈 
					a[top]=a[j]; //修改其对应的值 
				}
			}
		}
		printf("%d\n",ans);
	}
	return 0;
}