TensorFlo入门Google实战——chapter04
###part four 从定义损失函数开始
#EX03 自定义损失函数且完整的相应code
a=10
b=1
#loss=tf.reduce_sum(tf.where(tf.greater(v1,v2),(v1-v2)*a,(v2-v1)*b))
import tensorflow as tf
v1=tf.constant([1.0,2.0,3.0,4.0])
v2=tf.constant([4.0,3.0,2.0,1.0])
sess=tf.InteractiveSession()
print(tf.greater(v1,v2).eval(session=sess))
print(tf.where(tf.greater(v1,v2),v1,v2).eval(session=sess))
sess.close()[False False True True]
[4. 3. 3. 4.]#EX03 自定义损失函数且完整的相应code 以下是完整的code
import tensorflow as tf
from numpy.random import RandomState
batch_size=8
x=tf.placeholder(tf.float32,shape=(None,2),name='x_input')#两个输入节点
y_=tf.placeholder(tf.float32,shape=(None,1),name='y_input')#回归问题只有一个输出节点
w1=tf.Variable(tf.random_normal([2,1],stddev=1,seed=1))
y=tf.matmul(x,w1)#前向传播过程,简单的加权求和
#以下定义预测多了和预测少了的成本
loss_less=10
loss_more=1
loss=tf.reduce_sum(tf.where(tf.greater(y,y_),(y-y_)*loss_more,(y_-y)*loss_less)) #最新版的tensorflow中将tf.select()换成了tf.where()
train_step=tf.train.AdamOptimizer(0.001).minimize(loss)
#以下通过随机数生成一个模拟数据
rdm=RandomState(1)
dataset_size=128
X=rdm.rand(dataset_size,2) #给出真实输入值X
#给真实的数据加入均值为零的高斯噪声(-0.05——0.05的随机数)
Y=[[x1+x2+rdm.rand()/10.0-0.05] for (x1,x2) in X]
#训练神经网络
with tf.Session() as sess:
init_op=tf.initialize_all_variables()
sess.run(init_op)
STEPS=5000
for i in range(STEPS):
start=(i*batch_size) % dataset_size
end=min(start+batch_size,dataset_size)
sess.run(train_step,feed_dict={x:X[start:end],y_:Y[start:end]})
print(sess.run(w1))#EX04 学习率的设置
global_step=tf.Variable(0)
#通过exponential_decay函数生成学习率
learning_rate=tf.train.exponential_deacy(0.1,global_step,100,0.96,staircase=True)#利用指数衰减率来更新学习率。
#使用指数衰减的学习率。在minimize函数中传入global_step将自动更新global_step参数,从而使得学习率也得到相应更新。
learning_step=tf.train.GradientDescentOptimizer(learning_rate).minimize(mse,global_step=global_step)#在此利用梯度下降法进行更新参数。EX05 过拟合问题(一个实例问题)p79
#step1:生成模拟数据
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
data = []
label = []
np.random.seed(0) # 设置随机数生成时所用算法开始的整数值
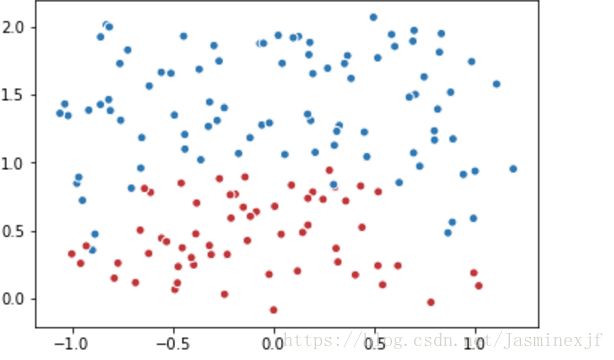
# 以原点为圆心,半径为1的圆把散点划分成红蓝两部分,并加入随机噪音。
for i in range(150):
x1 = np.random.uniform(-1,1) # 随机生成下一个实数,它在 [-1,1) 范围内。
x2 = np.random.uniform(0,2)
if x1**2 + x2**2 <= 1:
data.append([np.random.normal(x1, 0.1),np.random.normal(x2,0.1)])
label.append(0)
else:
data.append([np.random.normal(x1, 0.1), np.random.normal(x2, 0.1)])
label.append(1)
data = np.hstack(data).reshape(-1,2) # 把数据转换成n行2列
label = np.hstack(label).reshape(-1, 1) # 把数据转换为n行1列
plt.scatter(data[:,0], data[:,1], c=label,cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white")
plt.show()
#step2 通过集合计算一个5层神经网络带L2正则化的损失函数计算方法
#2. 定义一个获取权重,并自动加入正则项到损失的函数。
def get_weight(shape, lambda1):
var = tf.Variable(tf.random_normal(shape), dtype=tf.float32) # 生成一个变量
tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(lambda1)(var)) # add_to_collection()函数将新生成变量的L2正则化损失加入集合losses
return var # 返回生成的变量
#3. 定义神经网络。
keep_prob = tf.placeholder(tf.float32)
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))
sample_size = len(data)
# 每层节点的个数
layer_dimension = [2,10,5,3,1]
# 神经网络的层数
n_layers = len(layer_dimension)
# 这个变量维护前向传播时最深层的节点,开始的时候就是输入层
cur_layer = x
# 当前层的节点个数
in_dimension = layer_dimension[0]
# 循环生成网络结构
for i in range(1, n_layers):
out_dimension = layer_dimension[i] # layer_dimension[i]为下一层的节点个数
# 生成当前层中权重的变量,并将这个变量的L2正则化损失加入计算图上的集合
weight = get_weight([in_dimension, out_dimension], 0.003)
bias = tf.Variable(tf.constant(0.1, shape=[out_dimension])) # 偏置
cur_layer = tf.nn.relu(tf.matmul(cur_layer, weight) + bias) # 使用Relu激活函数
in_dimension = layer_dimension[i] # 进入下一层之前将下一层的节点个数更新为当前节点个数
y= cur_layer
# 在定义神经网络前向传播的同时已经将所有的L2正则化损失加入了图上的集合,这里是损失函数的定义。
mse_loss = tf.reduce_mean(tf.square(y_ - y)) # 也可以写成:tf.reduce_sum(tf.pow(y_ - y, 2)) / sample_size
tf.add_to_collection('losses', mse_loss) # 将均方误差损失函数加入损失集合
# get_collection()返回一个列表,这个列表是所有这个集合中的元素,在本样例中这些元素就是损失函数的不同部分,将他们加起来就是最终的损失函数
loss = tf.add_n(tf.get_collection('losses'))
#step3 训练不带正则化项的
# 4. 训练不带正则项的损失函数mse_loss。
# 定义训练的目标函数mse_loss,训练次数及训练模型
train_op = tf.train.AdamOptimizer(0.001).minimize(mse_loss)
TRAINING_STEPS = 40000
with tf.Session() as sess:
tf.global_variables_initializer().run() # 初始化所有的变量
for i in range(TRAINING_STEPS):
sess.run(train_op, feed_dict={x: data, y_: label})
if i % 2000 == 0:
print("After %d steps, mse_loss: %f" % (i,sess.run(mse_loss, feed_dict={x: data, y_: label})))
# 画出训练后的分割曲线
xx, yy = np.mgrid[-1.2:1.2:.01, -0.2:2.2:.01]
grid = np.c_[xx.ravel(), yy.ravel()]
probs = sess.run(y, feed_dict={x:grid})
probs = probs.reshape(xx.shape)
plt.scatter(data[:,0], data[:,1], c=label, cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white")
plt.contour(xx, yy, probs, levels=[.5], cmap="Greys", vmin=0, vmax=.1)
plt.show()
"""
#step4 训练带有正则化项的神经网络(对比)
#5. 训练带正则项的损失函数loss。
# 定义训练的目标函数loss,训练次数及训练模型
train_op= tf.train.AdamOptimizer(0.001).minimize(loss)
TRAINING_STEPS = 40000
with tf.Session() as sess:
tf.global_variables_initializer().run()
for i in range(TRAINING_STEPS):
sess.run(train_op,feed_dict={x: data, y_: label})
if i % 2000 == 0:
print("After %d steps, loss: %f" % (i, sess.run(loss, feed_dict={x: data})))
# 画出训练后的分割曲线
xx, yy = np.mgrid[-1:1:.01, 0:2:.01]
grid = np.c_[xx.ravel(), yy.ravel()]
probs = sess.run(y, feed_dict={x:grid})
probs = probs.reshape(xx.shape)
plt.scatter(data[:,0], data[:,1], c=label,cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white")
plt.contour(xx, yy, probs, levels=[.5], cmap="Greys", vmin=0, vmax=.1)
plt.show()
#运行时提示占位符被占用,即当前GPU已经被占用 InvalidArgumentError (see above for traceback): You must feed a value for placeholder tensor 'Placeholder_1' with dtype float and shape [?,1]
# [[Node: Placeholder_1 = Placeholder[dtype=DT_FLOAT, shape=[?,1], _device="/job:localhost/replica:0/task:0/device:CPU:0"]()]]
""" 
After 0 steps, mse_loss: 0.562751
After 2000 steps, mse_loss: 0.028438
After 4000 steps, mse_loss: 0.017321
After 6000 steps, mse_loss: 0.012790
After 8000 steps, mse_loss: 0.010860
After 10000 steps, mse_loss: 0.009956
After 12000 steps, mse_loss: 0.008558
After 14000 steps, mse_loss: 0.004825
After 16000 steps, mse_loss: 0.000109
After 18000 steps, mse_loss: 0.000000
After 20000 steps, mse_loss: 0.000000
After 22000 steps, mse_loss: 0.000000
After 24000 steps, mse_loss: 0.000000
After 26000 steps, mse_loss: 0.000000
After 28000 steps, mse_loss: 0.000000
After 30000 steps, mse_loss: 0.000000
After 32000 steps, mse_loss: 0.000000
After 34000 steps, mse_loss: 0.000000
After 36000 steps, mse_loss: 0.000000
After 38000 steps, mse_loss: 0.000000分析:最后一个报错可能是因为我没有安装可以并行处理的GPU版本的tensorflow
##另外一个例子(根据随机数据拟合一条直线(曲线拟合))
import tensorflow as tf
import numpy as np
# 使用 NumPy 生成假数据(phony data), 总共 100 个点.
x_data = np.float32(np.random.rand(2, 100)) # 随机输入
y_data = np.dot([0.100, 0.200], x_data) + 0.300 #真实的w;[0.100 0.200] b;[0.300]
# 构造一个线性模型
#
b = tf.Variable(tf.zeros([1]))
W = tf.Variable(tf.random_uniform([1, 2], -1.0, 1.0))
y = tf.matmul(W, x_data) + b
# 最小化方差
loss = tf.reduce_mean(tf.square(y - y_data))
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss)
# 初始化变量
init = tf.initialize_all_variables()
# 启动图 (graph)
sess = tf.Session()
sess.run(init)
# 拟合平面
for step in range(0, 201):
sess.run(train)
if step % 20 == 0:
print(step, sess.run(W), sess.run(b))
sess.close()0 [[0.5454072 0.3967377]] [-0.08817289]
20 [[0.21276881 0.2995818 ]] [0.18908072]
40 [[0.13007756 0.23834647]] [0.26394528]
60 [[0.10869605 0.21379201]] [0.28809068]
80 [[0.10266885 0.20480564]] [0.2960305]
100 [[0.10085183 0.20164813]] [0.2986703]
120 [[0.10027843 0.20056061]] [0.29955333]
140 [[0.10009224 0.20018987]] [0.29984975]
160 [[0.10003078 0.20006414]] [0.29994944]
180 [[0.10001031 0.20002162]] [0.299983]
200 [[0.10000346 0.20000726]] [0.2999943]import tensorflow as tf
from numpy.random import RandomState
# 1. 定义神经网络的参数,输入和输出节点
batch_size = 8
w1= tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2= tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))
x = tf.placeholder(tf.float32, shape=(None, 2), name="x-input")
y_= tf.placeholder(tf.float32, shape=(None, 1), name='y-input')
# 2. 定义前向传播过程,损失函数及反向传播算法
a = tf.matmul(x, w1)
y = tf.matmul(a, w2)
cross_entropy = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0)))
train_step = tf.train.AdamOptimizer(0.001).minimize(cross_entropy)
# 3. 生成模拟数据集
rdm = RandomState(1)
X = rdm.rand(128,2)
Y = [[int(x1+x2 < 1)] for (x1, x2) in X]
# 4. 创建一个会话来运行TensorFlow程序
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
# 输出目前(未经训练)的参数取值。
print("w1:", sess.run(w1))
print("w2:", sess.run(w2))
print("\n")
# 训练模型。
STEPS = 5000
for i in range(STEPS):
start = (i * batch_size) % 128
end = (i * batch_size) % 128 + batch_size
sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})
if i % 1000 == 0:
total_cross_entropy = sess.run(cross_entropy, feed_dict={x: X, y_: Y})
print("After %d training step(s), cross entropy on all data is %g" % (i, total_cross_entropy))
# 输出训练后的参数取值。
print("\n")
print("w1:", sess.run(w1))
print("w2:", sess.run(w2))
w1: [[-0.8113182 1.4845988 0.06532937]
[-2.4427042 0.0992484 0.5912243 ]]
w2: [[-0.8113182 ]
[ 1.4845988 ]
[ 0.06532937]]
After 0 training step(s), cross entropy on all data is 0.0674925
After 1000 training step(s), cross entropy on all data is 0.0163385
After 2000 training step(s), cross entropy on all data is 0.00907547
After 3000 training step(s), cross entropy on all data is 0.00714436
After 4000 training step(s), cross entropy on all data is 0.00578471
w1: [[-1.9618274 2.582354 1.6820376]
[-3.4681718 1.0698233 2.11789 ]]
w2: [[-1.8247149]
[ 2.6854665]
[ 1.418195 ]]
# 不同的损失函数会对训练模型产生重要影响
import tensorflow as tf
from numpy.random import RandomState
# 1. 定义神经网络的相关参数和变量
batch_size = 8
x = tf.placeholder(tf.float32, shape=(None, 2), name="x-input")
y_ = tf.placeholder(tf.float32, shape=(None, 1), name='y-input')
w1= tf.Variable(tf.random_normal([2, 1], stddev=1, seed=1))
y = tf.matmul(x, w1)
# 2. 设置自定义的损失函数
# 定义损失函数使得预测少了的损失大,于是模型应该偏向多的方向预测。
loss_less = 10
loss_more = 1
loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_) * loss_more, (y_ - y) * loss_less))
train_step = tf.train.AdamOptimizer(0.001).minimize(loss)
# 3. 生成模拟数据集
rdm = RandomState(1)
X = rdm.rand(128,2)
Y = [[x1+x2+(rdm.rand()/10.0-0.05)] for (x1, x2) in X]
# 4. 训练模型
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
STEPS = 5000
for i in range(STEPS):
start = (i*batch_size) % 128
end = (i*batch_size) % 128 + batch_size
sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})
if i % 1000 == 0:
print("After %d training step(s), w1 is: " % (i))
print(sess.run(w1), "\n")
print("[loss_less=10 loss_more=1] Final w1 is: \n", sess.run(w1))
After 0 training step(s), w1 is:
[[-0.81031823]
[ 1.4855988 ]]
After 1000 training step(s), w1 is:
[[0.01247112]
[2.1385448 ]]
After 2000 training step(s), w1 is:
[[0.45567414]
[2.1706066 ]]
After 3000 training step(s), w1 is:
[[0.69968724]
[1.8465308 ]]
After 4000 training step(s), w1 is:
[[0.89886665]
[1.2973602 ]]
[loss_less=10 loss_more=1] Final w1 is:
[[1.019347 ]
[1.0428089]]# 5. 重新定义损失函数,使得预测多了的损失大,于是模型应该偏向少的方向预测
loss_less = 1
loss_more = 10
loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_) * loss_more, (y_ - y) * loss_less))
train_step = tf.train.AdamOptimizer(0.001).minimize(loss)
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
STEPS = 5000
for i in range(STEPS):
start = (i*batch_size) % 128
end = (i*batch_size) % 128 + batch_size
sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})
if i % 1000 == 0:
print("After %d training step(s), w1 is: " % (i))
print(sess.run(w1), "\n")
print("[loss_less=1 loss_more=10] Final w1 is: \n", sess.run(w1))After 0 training step(s), w1 is:
[[-0.8123182]
[ 1.4835987]]
After 1000 training step(s), w1 is:
[[0.18643527]
[1.0739334 ]]
After 2000 training step(s), w1 is:
[[0.95444274]
[0.98088616]]
After 3000 training step(s), w1 is:
[[0.9557403]
[0.9806633]]
After 4000 training step(s), w1 is:
[[0.9546602 ]
[0.98135227]]
[loss_less=1 loss_more=10] Final w1 is:
[[0.9552581]
[0.9813394]]# 6. 定义损失函数为MSE
loss = tf.losses.mean_squared_error(y, y_)
train_step = tf.train.AdamOptimizer(0.001).minimize(loss)
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
STEPS = 5000
for i in range(STEPS):
start = (i*batch_size) % 128
end = (i*batch_size) % 128 + batch_size
sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})
if i % 1000 == 0:
print("After %d training step(s), w1 is: " % (i))
print(sess.run(w1), "\n")
print("[losses.mean_squared_error]Final w1 is: \n", sess.run(w1))结果:
After 0 training step(s), w1 is:
[[-0.81031823]
[ 1.4855988 ]]
After 1000 training step(s), w1 is:
[[-0.13337609]
[ 1.8130922 ]]
After 2000 training step(s), w1 is:
[[0.321903 ]
[1.5246348]]
After 3000 training step(s), w1 is:
[[0.67850214]
[1.2529727 ]]
After 4000 training step(s), w1 is:
[[0.89474 ]
[1.0859823]]
[losses.mean_squared_error]Final w1 is:
[[0.9743756]
[1.0243336]]#part()学习率部分
# 假设我们要最小化函数 $y=x^2$, 选择初始点$x_0=5$
# 1. 学习率为1的时候,x在5和-5之间震荡
import tensorflow as tf
TRAINING_STEPS = 10
LEARNING_RATE = 1
x = tf.Variable(tf.constant(5, dtype=tf.float32), name="x")
y = tf.square(x)
train_op = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(y)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(TRAINING_STEPS):
sess.run(train_op)
x_value = sess.run(x)
print("After %s iteration(s): x%s is %f."% (i+1, i+1, x_value)) #结果表明:此时学习率设置过大,在-5与5之间来回震荡
结果:
After 1 iteration(s): x1 is -5.000000.
After 2 iteration(s): x2 is 5.000000.
After 3 iteration(s): x3 is -5.000000.
After 4 iteration(s): x4 is 5.000000.
After 5 iteration(s): x5 is -5.000000.
After 6 iteration(s): x6 is 5.000000.
After 7 iteration(s): x7 is -5.000000.
After 8 iteration(s): x8 is 5.000000.
After 9 iteration(s): x9 is -5.000000.
After 10 iteration(s): x10 is 5.000000.
# 2. 学习率为0.001的时候,下降速度过慢,在901轮时才收敛到0.823355
TRAINING_STEPS = 1000
LEARNING_RATE = 0.001
x = tf.Variable(tf.constant(5, dtype=tf.float32), name="x")
y = tf.square(x)
train_op = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(y)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(TRAINING_STEPS):
sess.run(train_op)
if i % 100 == 0:
x_value = sess.run(x)
print("After %s iteration(s): x%s is %f."% (i+1, i+1, x_value)) #结果表明:此时的学习率过小。
After 1 iteration(s): x1 is 4.990000.
After 101 iteration(s): x101 is 4.084646.
After 201 iteration(s): x201 is 3.343555.
After 301 iteration(s): x301 is 2.736923.
After 401 iteration(s): x401 is 2.240355.
After 501 iteration(s): x501 is 1.833880.
After 601 iteration(s): x601 is 1.501153.
After 701 iteration(s): x701 is 1.228794.
After 801 iteration(s): x801 is 1.005850.
After 901 iteration(s): x901 is 0.823355.# 3. 使用指数衰减的学习率,在迭代初期得到较高的下降速度,可以在较小的训练轮数下取得不错的收敛程度
TRAINING_STEPS = 100
global_step = tf.Variable(0)
LEARNING_RATE = tf.train.exponential_decay(0.1, global_step, 1, 0.96, staircase=True) #指数学习率衰减 False:为连续学习率衰减率
x = tf.Variable(tf.constant(5, dtype=tf.float32), name="x")
y = tf.square(x)
train_op = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(y, global_step=global_step)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(TRAINING_STEPS):
sess.run(train_op)
if i % 10 == 0:
LEARNING_RATE_value = sess.run(LEARNING_RATE)
x_value = sess.run(x)
print("After %s iteration(s): x%s is %f, learning rate is %f."% (i+1, i+1, x_value, LEARNING_RATE_value))# 3. 使用指数衰减的学习率,在迭代初期得到较高的下降速度,可以在较小的训练轮数下取得不错的收敛程度
TRAINING_STEPS = 100
global_step = tf.Variable(0)
LEARNING_RATE = tf.train.exponential_decay(0.1, global_step, 1, 0.96, staircase=True) #指数学习率衰减 False:为连续学习率衰减率
x = tf.Variable(tf.constant(5, dtype=tf.float32), name="x")
y = tf.square(x)
train_op = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(y, global_step=global_step)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(TRAINING_STEPS):
sess.run(train_op)
if i % 10 == 0:
LEARNING_RATE_value = sess.run(LEARNING_RATE)
x_value = sess.run(x)
print("After %s iteration(s): x%s is %f, learning rate is %f."% (i+1, i+1, x_value, LEARNING_RATE_value))
# 3. 使用指数衰减的学习率,在迭代初期得到较高的下降速度,可以在较小的训练轮数下取得不错的收敛程度
TRAINING_STEPS = 100
global_step = tf.Variable(0)
LEARNING_RATE = tf.train.exponential_decay(0.1, global_step, 1, 0.96, staircase=True) #指数学习率衰减 False:为连续学习率衰减率
x = tf.Variable(tf.constant(5, dtype=tf.float32), name="x")
y = tf.square(x)
train_op = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(y, global_step=global_step)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(TRAINING_STEPS):
sess.run(train_op)
if i % 10 == 0:
LEARNING_RATE_value = sess.run(LEARNING_RATE)
x_value = sess.run(x)
print("After %s iteration(s): x%s is %f, learning rate is %f."% (i+1, i+1, x_value, LEARNING_RATE_value))结果:
After 1 iteration(s): x1 is 4.000000, learning rate is 0.096000.
After 11 iteration(s): x11 is 0.690561, learning rate is 0.063824.
After 21 iteration(s): x21 is 0.222583, learning rate is 0.042432.
After 31 iteration(s): x31 is 0.106405, learning rate is 0.028210.
After 41 iteration(s): x41 is 0.065548, learning rate is 0.018755.
After 51 iteration(s): x51 is 0.047625, learning rate is 0.012469.
After 61 iteration(s): x61 is 0.038558, learning rate is 0.008290.
After 71 iteration(s): x71 is 0.033523, learning rate is 0.005511.
After 81 iteration(s): x81 is 0.030553, learning rate is 0.003664.
After 91 iteration(s): x91 is 0.028727, learning rate is 0.002436.##part()滑动平均模型 一直处于不是太理解的懵懵状态
# 在采用随机梯度下降法训练神经网络模型时,滑动平均模型能够提高训练模型在测试数据上面的效果
import tensorflow as tf
# 1. 定义变量及滑动平均类
v1 = tf.Variable(0, dtype=tf.float32)
step = tf.Variable(0, trainable=False)
ema = tf.train.ExponentialMovingAverage(0.99, step)
maintain_averages_op = ema.apply([v1])
# 2. 查看不同迭代中变量取值的变化
with tf.Session() as sess:
# 初始化
init_op = tf.global_variables_initializer()
sess.run(init_op)
print(sess.run([v1, ema.average(v1)]))
# 更新变量v1的取值
sess.run(tf.assign(v1, 5))
sess.run(maintain_averages_op)
print(sess.run([v1, ema.average(v1)]))
# 更新step和v1的取值
sess.run(tf.assign(step, 10000))
sess.run(tf.assign(v1, 10))
sess.run(maintain_averages_op)
print(sess.run([v1, ema.average(v1)]))
# 更新一次v1的滑动平均值
sess.run(maintain_averages_op)
print(sess.run([v1, ema.average(v1)]))
[0.0, 0.0]
[5.0, 4.5]
[10.0, 4.555]
[10.0, 4.60945]