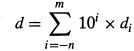CSI-III：信息的表示与处理-数值陷阱(二)

     本篇继续上一篇，进行浮点数的介绍，浮点数的表示并不像整型那样简单，其在计算机中的运算也会使用更多地时钟周期。我们都知道计算机并不能绝对正确的表示浮点数，都是在允许的精度范围内进行计算，这是由计算的信息表示方式(0和1)所决定的。所以，对于浮点数的误差，我们更应该谨慎和小心，这样才能够在编写的程序中避免可能的病态问题。

    谈到浮点数，或许你能想到IEEE(读作“Eye-Triple-Eee”)754标准。这个标准的制定是从1976年开始由Intel赞助的，在8087设计的同时，8087是一种为8086处理器提供浮点支持的芯片。他们请Kahan作为顾问，帮助设计未来处理器浮点标准。并支持Kahan加入IEEE委员会，后来IEEE最终制定的标准非常接近于Kahan为Intel设计的标准。这样IEEE754标准也就诞生了。

1. 二进制小数

        在理解浮点数之前我们先看下含有小数值的二进制数字。首先先看下我们所熟悉的十进制是如何来表示小数的，十进制表示法所使用的表示形式为：d_md_m-1…d₁d_0.d_-1d_-2…d_-n,其中每个十进制数di的取值为0~9，这个表示的数值d为：

                                                        

类似的，我们考虑形如b_mb_m-1…..b₁b₀.b_-1b_-2…b_-n-1b_-n的表示法，其中每个二进制数字bi的取值为0或者1，这种表示方法表示的数b定义如下：

2.IEEE浮点表示

IEEE浮点标准用V=(-1)^s×M×2^E的形式来表示一个浮点数。

符号s决定了这个数是负数(s=1)还是正数(s=0),对于数值0的符号作为特殊情况处理。

尾数 M是一个二进制小数，它的范围是1~2-ε，或者是0~1-ε

阶码E的作用是对浮点数加权，这个权重是2的E次幂(可能是负数)

将浮点数的位表示划分为三个字段，分别对这些值进行编码：

<1>.一个单独的符号位s直接编码符号s.

<2>.K位的阶码字段exp=ek-1….e1e0编码阶码E。

<3>.N位小数字段frac=fn-1….f1f0编码尾数M，并且编码出来的值也依赖于阶码字段的值是否等于0。

      在单精度浮点格式(float)中,s、exp和frac字段分别为1位，k=8位和n=23位，得到一个32位的表示。在双精度浮点格式(double)中，s、exp和frac的值分别为1位、k=11位和n=52位，得到一个64位的表示。

 

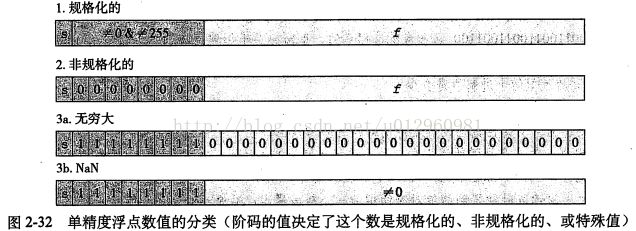
给定了位表示，根据exp的值，被编码的值可以分为三种情况。

 

下面我们讨论这三种情况：

(1).规格化

        当exp的位模式既不全为0(数值0)，也不全为1(单精度数值为255，双精度数值为2047)时，都属于这类情况。在这种情况中，阶码字段被解释为以偏置形式表示的有符号整数。也就是说，阶码的值是E=e-Bias,其中e是无符号数，其位表示为e_k-1…e₁e₀,而Bias是一个等于2^k-1-1(单精度是127，双精度是1023)的偏置值。由此产生指数的取值范围，对于单精度是-126~+127，对于双精度是-1022~+1023。

        对小数字段frac的解释为描述小数值f,其中0<=f<1,其二进制表示为0.fn-1…f1f0,也就是二进制小数点在最高有效位的左边。尾数定义为M=1+f.我们可以将M看成一个二进制表达式为1.fn-1fn-2…f0的数字。

(2)非规格化

      当阶码域为全0时，所表示的数就是非规格化形式，在这种情况下，阶码值E=1-Bias,而尾数的值是M=f，也就是小数字段的值，不包含隐含的开头的1.

这里的阶码值为1-Bias而不是简单的-Bias,后面我再介绍这么设置的原因。

(3).特殊值

       最后一类数值是当指阶码全为1的时候出现的。当小数域全为0时，得到的值表示无穷，当s=0时是+∞,或者当s=1时是-∞.当小数域为非零时，结果值被称为”NaN”,即不是一个数。

可能针对上面的概念描述，你可能还不够清楚浮点数具体是如何表示的，那么下面我们看一个数字实例，在这个实例中我们假定8位的浮点格式，其中有k=4的阶码位和n=3的小数位。那么偏置Bias=2^4-1-1=7，请看下图：

      上图只是非负值的浮点格式表示，从0自身开始，最靠近0的是给规格化数。这种格式的非规格数的E=1-7=-6，得到权2^E=1/64.小数f的值得范围是0,1/8,….7/8，从而得到数V的范围是0~1/64*7/8=7/512.

      同时，从上图中我们可以看到从最大的非规格化数7/512到最小的规格化数8/512的平滑转变，这就是我们为什么在非规格化数将E定义为1-Bias，而不是-Bias.

      当阶码增大时，我们就能够得到更大的规格化的值。当取到最大的规格化数时，阶码E=7，尾数M=1+f=1+7/8=15/8,此时的数值为V=2⁷*15/8=1992/8=240。

      通过上面的介绍，你一定熟悉了IEEE754是如何进行浮点数的编码的，下面我们再看一个使用32位浮点格式来对整数12345进行单精度的浮点数表示的例子：

我们知道了对于32位的单精度浮点数，其符号占1位，阶码E占8位，尾数M占23位。整数12345的二进制表示为[11 0000 0011 1001],通过将二进制小数点左移13位。我们得到这个数的规格化表示1.1 0000 0011 1001×2¹³,我们丢弃开头的1，并在末尾增加10个0，以构造小数位，得到的二进制表示为[1 0000 0011 1001 0000 0000 00]。为了构造阶码字段，我们用13加上偏置127,得到140，其二进制为[10001100],最后加上符号位0，我们得到这个数的浮点数二进制 表示为[010001100 1 0000 0011 1001 0000 0000 00]。我们观察到整数值12345和单精度浮点值12345.0在位级表示上有下列关系：

我们看到，浮点数尾数部分在整数表示的最高有效位1之前就停止了(这个位就是隐含的开头的位1)，和浮点表示的小数部分的高位是匹配的。

3.舍入

     计算机的表示方法限制了浮点数的范围和精度，浮点运算只能近似地表示实数运算。因此，对于值x，我们一般享用一种系统的方法，能够找到”最接近的”匹配值x’,它可以用期望的浮点形式表示出来。这就是舍入运算。IEEE浮点格式定义了四种不同的舍入方式：

     向偶数舍入、向零舍入、向下舍入、向上舍入。

     向偶数舍入也称为向最接近的值舍入，是默认的方式，试图找到一个最接近的匹配值。当值是两个可能结果的之间数值时，其采用的方法是：将数字向上或者向下舍入，使得结果的最低有效数字是偶数。因此，这种方法将1.5和2.5美元都舍入成2美元。

    有什么理由偏向取偶数呢？为什么不始终把位于两个可表示的值中间的值都向上舍入呢？假设有这样的场景：这组方法舍入一组数值，会在计算这些值的平均数中引入统计偏差。我们采用这种舍入得到的一组值得平均值将比这些数本身的平均值略高。相反，如果采用向下舍入，那么得到的平均值就略低。而向偶数舍入在大多数现实情况中避免了这种统计偏差。在50%的时间里，它将向下舍入，而在50%的时间里，它将向上舍入。

4.浮点运算

     在浮点运算中，浮点加法不具有结合性。例如，表达式(3.14+1e10)-1e10求值得到0.0—因为舍入,3.14会丢失。另一方面，表达式3.14+(1e10-1e10)得到值3.14.

     浮点乘法也遵循通常乘法所具有的许多属性。当同时由于可能发生溢出，或者由于舍入而失去精度，它不具有结合性。例如，在单精度浮点情况下，表达式(1e20*1e20)*1e-20的值为+∞,而1e20*(1e20*1e-20)将得出1e20.另外，浮点乘法在加法上不具备分配性。例如，在单精度浮点情况下，表达式1e20*(1e20-1e20)的值为0.0，而1e20*1e20-1e20*1e20会得到NaN.

5.C语言的浮点数

     C语言提供了两种不同的浮点数据类型：float和double。当int、float和double格式之间进行强制类型转换时，程序改变数值和位模式的原则如下：

(1)从int 转换成float，数字不会溢出，但是可能被舍入。

(2)从int 或者float转换成double,因为dobule有更大的范围和精度，所以能够保留精确的数值。

(3)从double转换成float，因为范围要小一些，所以值可能溢出为-∞或者+∞,另外，由于精度较小，它还可能被舍入。

(4)从float或者double转换成int，值将会向零舍入。