石器时代 —— Leetcode刷题日记 （一 百大热题）

Date: 2019.10.22 ～ (C++ Version)

All Labels:

热题100

L1 两数之和

一遍hash法

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int,int> m;
        for (int i = 0; i < nums.size(); i++) {
            if (m.count(target-nums[i])) return {m[target-nums[i]],i};
            m[nums[i]] = i;
        }
        return {-1,-1};
    }
};

L2 两数相加

新建一个链表，按照由低到高遍历相加

输入：(2 -> 4 -> 3) + (5 -> 6 -> 4)
输出：7 -> 0 -> 8
原因：342 + 465 = 807

暴力相加

暴力相加会导致 数据溢出！

class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        long long int sumNum = ListSum(l1) + ListSum(l2);
        string str = to_string(sumNum);
        reverseS(str);
        ListNode *head = new ListNode(str[0] - '0');
        ListNode *cur = head;
        int pos = 1;
        while (pos < str.size()) {
            ListNode *tmp = new ListNode(str[pos++]-'0');
            head->next = tmp;
            head = head->next;
        }
        return cur;
    }
    long long int ListSum(ListNode* node) {
        if (!node) return 0;
        return ListSum(node->next) * 10 + node->val;
    }
    void reverseS(string& str) {
        if (str.size() < 2) return;
        int i = 0, j = str.size() - 1;
        while (i < j) swap(str[i++], str[j--]);
    }
};

递归

class Solution {
private:
    ListNode* dummy;
public:
    Solution() {dummy = new ListNode(0);}
    ~Solution () {delete dummy;}
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        if (!11) l1 = new ListNode(0);
        if (!12) l2 = new ListNode(0);
        return assignList(l1, l2, 0);
    }
    ListNode* assignList(ListNode* l1, ListNode* l2, int carry) {
     // 注意中止条件! 包括l1和l2和进位值共同中止
        if (l1 == dummy && l2 == dummy && carry == 0) return NULL;
        if (!l1) return assignList(dummy, l2, carry);
        if (!l2) return assignList(l1, dummy, carry);
        int sum = l1->val + l2->val + carry;
        int x = sum % 10;
        int y = sum / 10;
        ListNode *newN = new ListNode(x);
        newN->next = assignList(l1->next, l2->next, y);
        return newN;
    }
};

迭代

class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
    	// dummy避免l1和l2均空 cur指向新链表
        ListNode* dummy = new ListNode(-1), *cur = dummy; 
        int carry = 0;
        while (l1 || l2)
        {
            int val1 = l1 ? l1->val : 0;
            int val2 = l2 ? l2->val : 0;
            int sum = val1 + val2 + carry;
            carry = sum / 10;
            cur->next = new ListNode(sum%10);
            cur = cur->next;
            if (l1) l1 = l1->next;
            if (l2) l2 = l2->next;
        }
        if (carry) cur->next = new ListNode(1);
        return dummy->next;
    }
};

L3 无重复字符的最长子串

经典滑动窗题目。
唯一注意的是max函数放置的位置！

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        if (s.size() < 2) return s.size();
        int left = 0, right = 0, maxLen = INT_MIN;
        unordered_set<char> win;
        while (right < s.size()) {
            win.emplace(s[right]);
            right++;
            // 唯一要点: max()放的位置!
            maxLen = max(maxLen, right - left); 
            while (!win.empty() && win.count(s[right])) {
                win.erase(s[left]);
                left++;
            }
        }
        return maxLen;
    }
};

L4 找两个升序数组中的中位数

润色理解

• 题目要求是对数复杂度，且两个数组都是升序，所以必然是二分查找的高级考察！
• 辅助函数设置为找两个序列中的第k大数，并设置双指针对两个数组进行查询！

代码

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int totalLen = nums1.size() + nums2.size();
        if (totalLen % 2) return helper(nums1,0,nums2,0,totalLen/2+1);
        else return 0.5 * (helper(nums1,0,nums2,0,totalLen/2) + 
            helper(nums1,0,nums2,0,totalLen/2+1));
    }
    int helper(vector<int>& nums1, int p, vector<int>& nums2, int q, int k) {
        // 寻找第k大的数
        if (p >= nums1.size()) return nums2[q+k-1];
        if (q >= nums2.size()) return nums1[p+k-1];
        if (k == 1) return min(nums1[p], nums2[q]);
        int half = k / 2;
        // 其中一个数组不够half个,则把另一个数组的前half个直接跳过
        // 因为第k个不会在那另一个数组的前half个(因为第一个数组不够数)
        int n1 = p + half - 1 < nums1.size() ? nums1[p + half - 1] : INT_MAX;
        int n2 = q + half - 1 < nums2.size() ? nums2[q + half - 1] : INT_MAX;
        if (n1 <= n2) return helper(nums1, p + half, nums2, q, k - half);
        else return helper(nums1, p, nums2, q + half, k - half);
    }
};

升级版 - 数组划分 - 不熟悉

• 合并后的有序数组可以分成两部分，左边比中位数小，右边比它大
• 总长度 len 可求，左边部分的长度也可以求：(len + 1) >> 1
• 我们观察左边，它是由 nums1 和 nums2 中前排较小的数组成，我们假设来源于 nums1 的左分段的长度为 partLen1 ，剩下的就是来源于 nums2 左分段，长度是 ((len + 1) >> 1) - partLen1
• 中位数由什么决定：nums1 左分段的最右项，叫 L1，nums2 左分段的最右项，叫 L2，nums1 右分段的最左项叫 R1，nums2 右分段的最左项叫 R2；只要求出 partLen1 ，这些项都能确定，它们确定了，中位数就能确定：① 如果合并后的数组是偶数的话，中位数等于 (Math.max(L1, L2) + Math.min(R1, R2)) / 2 ，② 如果是奇数，中位数等于Math.max(L1, L2)
  所以，怎么求 partLen1 呢？
• ① 在 nums1 把 partLen1 当做中位数求：nums1 数组是有序的，用二分查找，找出中位数。这个中位数可能不是想要的 partLen1，可能在这个中位数左边或右边
• ② 什么时候才是合适的：满足 L1 <= R2 && L2 <= R1。为什么？因为根据有序性，L1 是必定小于 L2，R1 是必定小于 R2，L1和R1是处于合并后数组的左边的，它必然小于右侧的R2和R1，二分查找的过程中满足该条件，就可以根据L1、L2、R2和R1求出中位数！
• ③ 如果不满足，就要移动指针，继续二分，直到找出满足条件的 partLen1

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size(), n = nums2.size();
        if (m < n) return findMedianSortedArrays(nums2, nums1);
        if (n == 0) return ((double)nums1[(m - 1) / 2] + (double)nums1[m / 2]) / 2.0;
        int left = 0, right = n * 2;
        while (left <= right) {
            int mid2 = (left + right) / 2;
            int mid1 = m + n - mid2;
            double L1 = mid1 == 0 ? INT_MIN : nums1[(mid1 - 1) / 2];
            double L2 = mid2 == 0 ? INT_MIN : nums2[(mid2 - 1) / 2];
            double R1 = mid1 == m * 2 ? INT_MAX : nums1[mid1 / 2];
            double R2 = mid2 == n * 2 ? INT_MAX : nums2[mid2 / 2];
            if (L1 > R2) left = mid2 + 1;
            else if (L2 > R1) right = mid2 - 1;
            else return (max(L1, L2) + min(R1, R2)) / 2;
        }
        return -1;
    }
};

L5 最长回文子串

扩散搜索

class Solution {
public:
    string longestPalindrome(string s) {
        if (s.size() < 2) return s; // 0 1
        int n = s.size(), maxLen = 0, start = 0;
        for (int i = 0; i < n - 1; i ++)
        { // 回文串的长度可奇可偶，比如 "bob" 是奇数形式的回文，"noon" 就是偶数形式的回文，
          // 两种形式的回文都要搜索，对于奇数形式的，我们就从遍历到的位置为中心，向两边进行扩散
          // 对于偶数情况，我们就把当前位置和下一个位置当作偶数行回文的最中间两个字符，
          // 然后向两边进行搜索!
            searchPalindrome(s, i, i, start, maxLen); // even
            searchPalindrome(s, i, i+1, start, maxLen); // odd
        }
        return s.substr(start, maxLen);
    }
    void searchPalindrome(string s, int left, int right, int& start, int& maxLen)
    {
        while(left >= 0 && right < s.size() && s[left] == s[right])
        { // 左右扩散 判断左右相等
            --left; 
            ++right;
        }
        if (maxLen < right - left - 1)
        {
            start = left + 1;
            maxLen = right - left - 1;
        }
    }
};

合并成一个函数 已经提升了很多 4 ms 8.9 MB —— BEST Algorithm of Four Method!

class Solution {
public:
    string longestPalindrome(string s) {
        if (s.size() < 2) return s;
        int n = s.size(), maxLen = 0, start = 0;
        for (int i = 0; i < n;)
        {
            if (n - i <= maxLen / 2) break;
            int left = i, right = i;
            while (right < n - 1 && s[right + 1] == s[right]) 
            { // 先向右遍历跳过重复项, 如noon，i在第一个o的位置，
              // 如果我们以o为最中心往两边扩散，是无法得到长度为4的回文串的
            	++right;
            }
            // 之后left指向第一个o，right指向第二个o，然后再向两边扩散
            i = right + 1; // 循环迭代
            while (right < n - 1 && left > 0 && s[right + 1] == s[left - 1])
            {
                ++right; --left;
            }
            if (maxLen < right - left + 1)
            {
                maxLen = right - left + 1;
                start = left;
            }
        }
        return s.substr(start, maxLen);
    }
};

动态规划

• dp[i, j]表示字符串i到j是否为回文串∈{0, 1}

dp[i, j] = 1                                 if i == j
         = s[i] == s[j]                      if j = i + 1
         = s[i] == s[j] && dp[i + 1][j - 1]  if j > i + 1      

• 从dp[i+1][j-1] 到 dp[i][j], 所以有两种遍历方法！
• ① 斜着遍历，先从字符串长度len: 1>n，在左边界0~n-len;

class Solution {
public:
    string longestPalindrome(string s) {
        if (s.size() < 2) return s;
        int N = s.size();
        vector<vector<int>> dp(N,vector<int>(N, false));
        int maxLen = INT_MIN, start = -1;
        string res = "";
        for (int len = 1; len <= N; len++) {
            for (int i = 0; i <= N - len; i++) {
                int j = i + len - 1;
                dp[i][j] = (s[i] == s[j]) && (j - i < 2 || dp[i+1][j-1]);
                if (dp[i][j] && maxLen < j - i + 1) {
                    maxLen = j - i + 1;
                    start = i;
                } 
            }
        }
        return s.substr(start, maxLen);
    }
};

• ② i: n->0; j: i->n

class Solution {
public:
    string longestPalindrome(string s) {
        if (s.empty()) return "";
        int n = s.size(), dp[n][n] = {0}, left = 0, len = 1; 
        // 二维数组由 int 改为 vector 后，就会超时
        for (int i = 0; i < n; i++)
        {
            dp[i][i] = 1;
            for (int j = 0; j < i; j ++)
            {
                // 递推公式
                dp[j][i] = (s[i] == s[j] && (i - j < 2 || dp[j + 1][i - 1]));
                if (dp[j][i] && len < i - j + 1)
                {
                    len = i - j + 1;
                    left = j;
                }
            }
        }
        return s.substr(left, len);
    }
};

马拉车算法/Manacher’s Algorithm

• 线性复杂度 O(n)！

class Solution {
public:
    string longestPalindrome(string s) {
        string t ="$#";
        for (int i = 0; i < s.size(); ++i) {
            t += s[i];
            t += '#';
        }
        int p[t.size()] = {0}, id = 0, mx = 0, resId = 0, resMx = 0;
        // id 为能延伸到最右端的位置的那个回文子串的中心点位置
        // mx 是回文串能延伸到的最右端的位置
        for (int i = 1; i < t.size(); ++i) {
            p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;
            while (t[i + p[i]] == t[i - p[i]]) ++p[i];
            if (mx < i + p[i]) {
                mx = i + p[i];
                id = i;
            }
            if (resMx < p[i]) {
                resMx = p[i];
                resId = i;
            }
        }
        return s.substr((resId - resMx) / 2, resMx - 1);
    }
};

1 每一个字符的左右都加上一个特殊字符，比如加上 ‘#’！ 奇偶规范化！
2 每个字符串第一位加‘$’, 字符串定位的原因 不能小于0
3 马拉车算法解析

L10 正则表达式匹配

暴力递归

class Solution {
public:
    bool isMatch(string s, string p) {
        if (p.empty()) return s.empty();
        bool flag = !s.empty() && (p[0] == '.' || p[0] == s[0]);
        if (p.size() > 1 && p[1] == '*') 
            return isMatch(s, p.substr(2)) || (flag && isMatch(s.substr(1),p));
        else return flag && isMatch(s.substr(1),p.substr(1));
    }
};

递归 + 备忘录

class Solution {
public:
    bool isMatch(string s, string p) {
        int x = s.size(), y = p.size();
        vector<vector<int>> memo(x+1, vector<int>(y, -1));
        return isMatch2(s,p,0,0,memo);
    }
    bool isMatch2(string& s, string& p, int i, int j, vector<vector<int>>& memo) {
        if (j >= p.size()) return i >= s.size();
        if (memo[i][j] > -1) 
            return memo[i][j];
        bool flag = i < s.size() && (p[j] == s[i] || p[j] == '.');
        if (j+1 < p.size() && p[j+1] == '*') 
            return memo[i][j] = isMatch2(s,p,i,j+2,memo) || 
                                (flag&&isMatch2(s,p,i+1,j,memo));
        else return memo[i][j] = flag&&isMatch2(s,p,i+1,j+1,memo);
    }
};

DP

• 注意细节：-2-1和迭代的过程不同
• 该题经典的思路就是定义二维DP数组: 元素dp[i][j]表示s[0,j)和p[0,j)是否匹配！

if p[j-1]!=*
    当s[i-1]=p[j-1]: dp[i][j]=dp[i-1][j-1]
else
    *重复0次: dp[i,j]=dp[i,j-2]
    *重复1次或多次: 当s[i-1]==p[j-2]: dp[i,j]=dp[i-1,j]

class Solution {
public:
    bool isMatch(string s, string p) {
        
        int len1 = s.size(), len2 = p.size();
        vector<vector<int>> dp(len1+1, vector<int>(len2+1, false));
        dp[0][0] = true;
        for (int i = 0; i <= len1; i++) {
            for (int j = 1; j <= len2; j++) { // 从p的第二个数开始
                if (j > 1 && p[j - 1] == '*')
                    dp[i][j] = dp[i][j-2] || 
                        (i>0 && (s[i-1]==p[j-2] || p[j-2]=='.') && dp[i-1][j]);
                else dp[i][j] = i>0 && (s[i-1]==p[j-1] || p[j-1]=='.') && dp[i-1][j-1];
            }
        }
        return dp.back().back();
    }
};

L11 盛最多水的容器

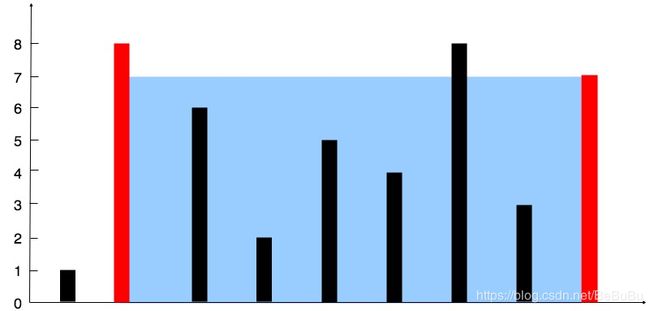
数据: n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 求delta_i * delta_Ai

双指针

• 双指针典型用法，每次移动左右指针中高度较小的指针！

class Solution {
public:
    int maxArea(vector<int>& height) {
        //
        int left = 0, right = height.size() - 1;
        int maxSum = INT_MIN;
        while (left < right) {
            int ht = min(height[left],height[right]);
            maxSum = max(maxSum, ht*(right-left));
            if (ht == height[left]) left++;
            else right--;
        }
        return maxSum;
    }
};

L15 三数之和

给定一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？找出所有满足条件且不重复的三元组。

双指针

• 双指针寻找后两个数
• 重点在如何去重！

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        if (nums.size() < 3) return {};
        vector<vector<int>> res;
        sort(nums.begin(), nums.end());
        for (int i = 0; i < nums.size() - 2; i++) {
            if (i > 0 && nums[i-1] == nums[i]) continue; // 去重1
            int left = i + 1, right = nums.size() - 1;
            int twoSum = -nums[i];
            while (left < right) {
                int tmp = nums[left] + nums[right];
                if (tmp == twoSum) {
                    res.push_back({-twoSum,nums[left],nums[right]});
                    // 去重2
                    while (left < right && nums[left+1] == nums[left]) left++;
                    while (left < right && nums[right] == nums[right-1]) right--;
                    //
                    left++; right--;
                }
                else if (tmp > twoSum) right--;
                else left++;
            }
        }
        return res;
    }
};

L17 电话号码的字母组合

Input: “23”
Output: [“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”].

回溯

• 回溯的经典例题
• 排列之类的都是回溯

class Solution {
public:
    vector<string> letterCombinations(string digits) {
        if (digits.empty()) return {};
        vector<string> res;
        vector<string> dict{"","","abc","def","ghi","jkl",
                            "mno","pqrs","tuv","wxyz"};
        combinationDFS(digits, dict, 0, "", res);
        return res;
    }
    void combinationDFS(string& digits, vector<string>& dict, int level, string out, vector<string>& res)
    {
        if (level == digits.size()) {res.push_back(out); return;}
        string str = dict[digits[level] - '0'];
        for (int i = 0; i < str.size(); i++)
            combinationDFS(digits, dict, level + 1, out + str[i], res);
    }
};

迭代

• 三层for循环

class Solution {
public:
    vector<string> letterCombinations(string digits) {
        if (digits.empty()) return {};
        vector<string> dict{"","","abc","def","ghi","jkl",
                            "mno","pqrs","tuv","wxyz"};
        vector<string> res = {""};
        for (int i = 0; i < digits.size(); i++) {
            string curStr = dict[digits[i] - '0'];
            vector<string> tmp;
            for (int j = 0; j < curStr.size(); ++j) {
                for (string s : res) tmp.push_back(s+curStr[j]);
            }
            res = tmp;
        }
        return res;
    }
};

L19 删除链表倒数第N个点

后序遍历 + 标记指针(单指针)

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode *label = new ListNode(-1);
        search(head, n, label);
        return label->next;
    }
    void search(ListNode *node, int &n, ListNode *&label) {
        if (!node) return;
        search(node->next, n, label);
        n--;
        if (label) node->next = label->next;
        if (n != 0) label->next = node;
    }
};

快慢指针

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        if (!head->next) return NULL;
        ListNode *pre = head, *cur = head;
        for (int i = 0; i< n; i++) cur = cur->next;
        if (!cur) return head->next;
        while (cur->next)
        {
            cur = cur->next;
            pre = pre->next;
        }
        pre->next = pre->next->next;
        return head;
    }
};

L20 合法括号

栈法

class Solution {
public:
    bool isValid(string s) {
        if ((int)s.size() % 2) return false;
        stack<char> savers;
        for (int i = 0; i < s.size(); i++)
        {
            char cur = s[i];
            if (cur == '(' || cur == '{' || cur == '[') savers.push(cur);
            else {
                if (savers.empty()) return false;
                if (cur == ')' && savers.top() != '(') return false;
                if (cur == ']' && savers.top() != '[') return false;
                if (cur == '}' && savers.top() != '{') return false;
                savers.pop();
            }
        }
        return savers.empty();
    }
};

L21 合并两个有效链表

Input: 1->2->4, 1->3->4
Output: 1->1->2->3->4->4

循环 dummy指针

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        if (!l1) return l2;
        if (!l2) return l1;
        ListNode *dummy = new ListNode(-1), *cur = dummy;
        while (l1 && l2) 
        {
            if (l1->val < l2->val) {cur->next = l1; l1 = l1->next;}
            else {cur->next = l2; l2 = l2->next;}
            cur = cur->next;
        }
        cur->next = (!l1&&!l2) ? NULL : (l1 ? l1 : l2);
        return dummy->next;
    }
};

递归

复杂度类似！

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        if (!l1) return l2;
        if (!l2) return l1;
        ListNode *newH = NULL;
        if (l1->val < l2->val) {newH = l1; l1 = l1->next;}
        else {newH = l2; l2 = l2->next;}
        newH->next = mergeTwoLists(l1, l2);
        return newH;
    }
};
}

简约递归形式

ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
    if (!l1 || (l2 && l1->val > l2->val)) swap(l1, l2);
    if (l1) l1->next = mergeTwoLists(l1->next, l2);
    return l1;
}

L22 生成括号

递归

class Solution {
public:
    vector<string> generateParenthesis(int n) {
        if (n < 1) return {};
        vector<string> res;
        backtrack(res, n, n, "");
        return res;
    }
    void backtrack(vector<string>& res, int n, int m, string tmp) {
        if (n > m) return; // 效果等价于isValidStr
        if (n == 0 && m == 0 /*&& isValidStr(tmp)*/)
            res.push_back(tmp);
        if (n > 0) backtrack(res, n-1, m, tmp+"(");
        if (m > 0) backtrack(res, n, m-1, tmp+")");
    }
    bool isValidStr(string& str) {
        int left = 0;
        for (auto& c : str) {
            if (c == '(') left++;
            else left--;
            if (left < 0) return false;
        }
        return left == 0;
    }
};

其他

W2 Special Way - 来自cc150 这里只是记录一下，太trick的方法先不记 只有一次递归的位置, 时间和空间会好点！

class Solution {
public:
    vector<string> generateParenthesis(int n) {
        unordered_set<string> st;
        if (n == 0) st.insert("");
        else {
            vector<string> pre = generateParenthesis(n - 1);
            for (auto a : pre) {
                for (int i = 0; i < a.size(); ++i) {
                    if (a[i] == '(') {
                        a.insert(a.begin() + i + 1, '(');
                        a.insert(a.begin() + i + 2, ')');
                        st.insert(a);
                        a.erase(a.begin() + i + 1, a.begin() + i + 3);
                    }
                }
                st.insert("()" + a);
            }
        }
        return vector<string>(st.begin(), st.end());
    }
};

- BFS - DP 方法 - TODO ！！

• DP状态转移方程： dp[i] = “(” + dp[可能的括号对数] + “)” + dp[剩下的括号对数]
• dp[i] = “(” + dp[j] + “)” + dp[i- j - 1] , j = 0, 1, …, i - 1

L23 合并k个排序链表

优先队列

class Solution {
private:
    class cmp {
    public:
        bool operator() (ListNode*& a, ListNode*& b) const {
            return a->val > b->val;
        }
    };
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        if (lists.empty()) return NULL;
        priority_queue<ListNode*, vector<ListNode*>, cmp> p_que;
        ListNode *dummy = new ListNode(-1);
        ListNode *cur = dummy;
        for (auto& x : lists)
            if (x) p_que.push(x);
        while (!p_que.empty()) {
            auto x = p_que.top(); p_que.pop();
            dummy->next = x;
            dummy = dummy->next;
            if (x->next) p_que.push(x->next);
        }
        return cur->next;
    }
};

分治法

class Solution {
public:
    ListNode* merge2List(ListNode* p, ListNode* q) {
        if (!p) return q;
        if (!q) return p;
        if (p->val <= q->val) {p->next = merge2List(p->next, q); return p;}
        else {q->next = merge2List(p, q->next); return q;}
    }
    ListNode* mergeKLists2(vector<ListNode*>& lists, int start, int end) {
        int len = lists.size();
        if (start > end) return NULL;
        if (start == end) return lists[start];
        int mid = start + (end - start) / 2;
        auto x = mergeKLists2(lists, start, mid);
        auto y = mergeKLists2(lists, mid+1, end);
        return merge2List(x, y); 
    }
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        return mergeKLists2(lists, 0, lists.size() - 1);
    }
};

其他

W3 . 混合排序 + 计数排序

class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        ListNode *dummy = new ListNode(-1), *cur = dummy;
        unordered_map<int, int> m;
        int mx = INT_MIN, mn = INT_MAX;
        for (auto node : lists) {
            ListNode *t = node;
            while (t) {
                mx = max(mx, t->val);
                mn = min(mn, t->val);
                ++m[t->val];
                t = t->next;
            }
        }
        for (int i = mn; i <= mx; ++i) {
            if (!m.count(i)) continue;
            for (int j = 0; j < m[i]; ++j) {
                cur->next = new ListNode(i);
                cur = cur->next;
            }
        }
        return dummy->next;
    }
};

L31 下一个排列

实现获取下一个排列的函数，算法需要将给定数字序列
重新排列成字典序中下一个更大的排列。
如果不存在下一个更大的排列，则将数字重新排列成最
小的排列（即升序排列）。In-Plane

In-Plane

class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        if (nums.size() < 2) return;
        int pos = nums.size() - 2;
        for (;pos >= 0;pos--)
            if (nums[pos] < nums[pos+1]) break;
        if (pos >= 0) {
            sort(nums.begin(), nums.end());
            return;
        }
        int pos2 = nums.size() - 1;
        for (; pos2 > pos; pos2--)
            if (nums[pos2] > nums[pos]) break;
        swap(nums[pos], nums[pos2]);
        sort(nums.begin()+pos+1, nums.end());        
    }
};

class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        int n = nums.size(), i = n - 2, j = n - 1;
        while (i >= 0 && nums[i] >= nums[i + 1]) --i;
        if (i >= 0)
        {
            while (nums[j] <= nums[i]) --j;
            swap(nums[i], nums[j]);
        }
        reverse(nums.begin() + i + 1, nums.end());
    }
};

STL 函数

class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        vector<int> res;
        if (!next_permutation(nums.begin(), nums.end())) 
            sort(nums.begin(), nums.end());
    }
}; 

L32 最长有效括号

给定一个只包含 ‘(’ 和 ‘)’ 的字符串，找出最长的包含有效括号的子串的长度。
输入: “)()())”
输出: 4
解释: 最长有效括号子串为 “()()”

暴力法

TLE

class Solution {
public:
    int longestValidParentheses(string s) {
        int maxLen = 0;
        for (int i = 0; i < s.size(); i++) {
            for (int j = i + 1; j < s.size(); j++) {
                if (isValid(s.substr(i,j-i+1)) && maxLen < j-i+1)
                    maxLen = j - i + 1;
            }
        }
        return maxLen;
    }
    bool isValid(string s) {
        int left = 0;
        for (auto& c : s) {
            if (c == '(') left++;
            else left--;
            if (left < 0) return false;
        }
        return left == 0;
    }
};

Stack

class Solution {
public:
    int longestValidParentheses(string s) {
        if (s.size() < 2) return 0;
        int maxLen = 0;
        stack<int> st;
        st.push(-1); // 记录不合法的终点
        for (int i = 0; i < s.size(); i++) {
            if (s[i] == '(') st.push(i);
            else {
                st.pop();
                if (st.empty()) st.push(i); // 记录不合法的终点 ')'
                else maxLen = max(maxLen, i - st.top());
            }
        }
        return maxLen;
    }
};

DP

class Solution {
public:
    int longestValidParentheses(string s) {
        if (s.size() < 2) return 0;
        vector<int> dp(s.size(), 0);
        int maxLen = 0;
        for (int i = 1; i < s.size(); i++) {
            if (s[i-1] == '(' && s[i] == ')') // "...()"
                dp[i] = i>=2 ? dp[i-2] + 2 : 2;
            if (s[i-1] == ')' && s[i] == ')') // "...))"
                if (i - dp[i-1] - 1 >= 0 && s[i - dp[i-1] - 1] == '(')
                    dp[i] = dp[i-1] + (i-dp[i-1]-2>=0 ? dp[i-dp[i-1]-2] : 0) + 2;
            maxLen = max(maxLen, dp[i]);
        }
        return maxLen;
    }
};

双遍历

是对isValid函数思想的拓展实现了该题！

class Solution {
public:
    int longestValidParentheses(string s) {
        if (s.size() < 2) return 0;
        int maxLen = 0;
        // 从左到右
        int left = 0, start = -1;
        for (int i = 0; i < s.size(); i++) {
            if (s[i] == '(') left++;
            else left--;
            if (left == 0) maxLen = max(maxLen, i - start);
            else if (left < 0) {
                start = i;
                left = 0;
            }
        }
        // 从右到左
        int right = 0, end = s.size(); 
        for (int i = s.size() - 1; i >= 0; i--) {
            if (s[i] == '(') right--;
            else right++;
            if (right == 0) maxLen = max(maxLen, end - i);
            else if (right < 0) {
                end = i;
                right = 0;
            }
        }
        return maxLen;
    }
};

L33 搜索旋转排序数组

输入: nums = [4,5,6,7,0,1,2], target = 0
输出: 4
PS：一维循环数组

二分查找

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0, right = nums.size() - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) return mid;
            else if (nums[mid] > nums[right]) {
                if (target < nums[mid] && target >= nums[left]) // 找有序
                    right = mid - 1;
                else left = mid + 1;
            } else {
                if (target > nums[mid] && target <= nums[right]) // 找有序
                    left = mid + 1;
                else right = mid - 1;
            }
        }
        return -1;
    }
};

L34 在排序数组中查找元素的第一个和最后一个位置

给定一个按照升序排列的整数数组 nums，和一个目标值 target。
找出给定目标值在数组中的开始位置和结束位置。
你的算法时间复杂度必须是 O(log n) 级别。 -> 二分法
如果数组中不存在目标值，返回 [-1, -1].

• 最简单思路是先找到，再左右搜索，最坏O(n)，一个数

寻找左右边界

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        vector<int> res;
        res.push_back(searchLeftBound(nums, target));
        res.push_back(searchRightBound(nums, target));
        return res;
    }
    int searchLeftBound(vector<int>& nums, int target) {
        int left = 0, right = nums.size();
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) right = mid;
            else if (nums[mid] > target) right = mid;
            else left = mid + 1;
        }
        if (right < 0 || right >= nums.size()) return -1;
        if (nums[right] == target) return right;
        return -1;
    }
    int searchRightBound(vector<int>& nums, int target) {
        int left = 0, right = nums.size();
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) left = mid + 1;
            else if (nums[mid] > target) right = mid;
            else left = mid + 1;
        }
        if (left - 1 < 0 || left - 1 >= nums.size()) return -1;
        if (nums[left - 1] == target) return left - 1;
        return -1;
    }
};

L39 组合求和

输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[[7], [2,2,3]]
说明：
所有数字（包括 target）都是正整数。
解集不能包含重复的组合。

回溯

class Solution {
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<vector<int>> res;
        vector<int> tmp;
        // sort(candidates.begin(), candidates.end());
        backtrack(candidates, res, tmp, 0, target, 0);
        return res;
    }
    void backtrack(vector<int>& candidates, vector<vector<int>>& res, 
        vector<int>& tmp, int sum, int target, int pos) {
        if (sum > target) return;
        if (sum == target) {
            res.push_back(tmp);
            return;
        }
        for (int i = pos; i < candidates.size(); i++) {
            int c = candidates[i];
            tmp.push_back(c); // sum没必要回溯
            backtrack(candidates, res, tmp, sum+c, target,i);
            tmp.pop_back();
        }
    }
};

迭代

class Solution {
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<vector<vector<int>>> dp;
        sort(candidates.begin(), candidates.end());
        for (int i = 1; i <= target; ++i) {
            vector<vector<int>> cur;
            for (int j = 0; j < candidates.size(); ++j) {
                if (candidates[j] > i) break;
                if (candidates[j] == i) {cur.push_back({candidates[j]}); break;}
                for (auto a : dp[i - candidates[j] - 1]) {
                    if (candidates[j] > a[0]) continue;
                    a.insert(a.begin(), candidates[j]);
                    cur.push_back(a);
                }
            }
            dp.push_back(cur);
        }
        return dp[target - 1];
    }
};

L42 接雨水

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

双指针遍历

• 原始
  water[i] = min(max(height[0…i]),max(height[i…end]))-height[i]
  ------------ 左边最高的柱子------------ 右边最高的柱子

class Solution {
public:
    int trap(vector<int>& height) {
        if (height.size() < 3) return 0;
        vector<int> leftMax(height.size(), 0);
        vector<int> rightMax(height.size(), 0);
        int res = 0;
        leftMax[0] = height[0];
        rightMax.back() = height.back();
        for (int j = 1; j < height.size(); j++) 
            leftMax[j] = max(leftMax[j-1], height[j]);
        for (int j = height.size() - 2; j >= 0; j--) 
            rightMax[j] = max(rightMax[j+1], height[j]);
        for (int i = 0; i < height.size(); i++)
            res += min(leftMax[i],rightMax[i]) - height[i];
        return res;
    }
};

• 双指针

class Solution {
public:
    int trap(vector<int>& height) {
        if (height.size() < 3) return 0;
        int left = 0, right = height.size() - 1;
        int l_max = INT_MIN, r_max = INT_MIN;
        int res = 0;
        while (left <= right) {
            l_max = max(l_max, height[left]);
            r_max = max(r_max, height[right]);
            if (l_max < r_max) res += l_max - height[left++];
            else res += r_max - height[right--]; 
        }
        return res;
    }
};

单调栈

class Solution {
public:
    int trap(vector<int>& height) { // 找坑法
        stack<int> st;
        int i = 0, res = 0;
        int n = height.size();
        while (i < n) {
            if (st.empty() || height[i] <= height[st.top()]) {
                st.push(i++); // 坑下降
            }
            else { // 坑上升
                int t = st.top(); st.pop();
                if (st.empty()) continue;
                res += (
                    min(height[i], height[st.top()]) - height[t]
                ) * (i - st.top() - 1);
            }
        }
        return res;
    }
};

L46 全排列

给定一个没有重复数字的序列，返回其所有可能的全排列。

熟练使用STL库

class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> res;
        sort(nums.begin(), nums.end());
        res.push_back(nums);
        while (next_permutation(nums.begin(), nums.end()))
            res.push_back(nums);
        return res;
    }
};

回溯1

class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        if (nums.empty()) return {};
        vector<vector<int>> res;
        vector<int> tmp;
        vector<bool> visited(nums.size(), false);
        backtrack(res,nums,tmp,visited);
        return res;
    }
    void backtrack(vector<vector<int>>& res, vector<int>& nums, vector<int>& tmp,                    vector<bool>& visited) {
        if (tmp.size() == nums.size()) res.push_back(tmp);
        for (int i = 0; i < nums.size(); i++) {
            if (visited[i]) continue;
            visited[i] = true;
            tmp.push_back(nums[i]);
            backtrack(res,nums,tmp,visited);
            tmp.pop_back();
            visited[i] = false;
        }
    }
};

回溯2

class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> res;
        permuteDFS(nums, 0, res);
        return res;
    }
    void permuteDFS(vector<int>& nums, int start, 
                    vector<vector<int>>& res)
    {
        // 这里不用写return也行 因为下面的for循环进不去
        if (start >= nums.size()) res.push_back(nums);
        for (int i = start; i < nums.size(); ++i) { // 循环情况下不用剪枝
            swap(nums[start], nums[i]);
            permuteDFS(nums, start + 1, res);
            swap(nums[start], nums[i]);            
        }
    }
};

递归插入法

class Solution {
public:
    vector<vector<int>> permute(vector<int>& num) {
        if (num.empty()) return vector<vector<int>>(1, vector<int>());
        vector<vector<int>> res;
        int first = num[0];
        num.erase(num.begin());
        vector<vector<int>> words = permute(num);
        for (auto &a : words) {
            for (int i = 0; i <= a.size(); ++i) {
                a.insert(a.begin() + i, first);
                res.push_back(a);
                a.erase(a.begin() + i);
            }
        }   
        return res;
    }
};

迭代法

都是在现有的排列的基础上，每个空位插入一个数字 和上面的思路一样？
TODO

class Solution {
public:
    vector<vector<int>> permute(vector<int>& num) {
        vector<vector<int>> res{{}};
        for (int a : num) {
            for (int k = res.size(); k > 0; --k) {
                vector<int> t = res.front();
                res.erase(res.begin());
                for (int i = 0; i <= t.size(); ++i) {
                    vector<int> one = t;
                    one.insert(one.begin() + i, a);
                    res.push_back(one);
                }
            }
        }
        return res;
    }
};

L48 旋转图像

对nxn图像进行顺时针旋转90度

转置+水平反转

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                swap(matrix[i][j], matrix[j][i]);
            }
            reverse(matrix[i].begin(), matrix[i].end());
        }
    }
};

循环替换

• 找到坐标变换的公式！
• 顺时针旋转：
  $$\begin{gathered} [x][y] \\ ->(90^o)->[y][n-1-x] \\ ->(90^o)->[n-1-x][n-1-y] \\ ->(90^o)->[n-1-y][x] \end{gathered}$$
• 逆时针旋转：
  $$[x][y]->(90^o)->[n-1-y][x]$$

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        for (int i = 0; i < n / 2; ++i) {
            for (int j = i; j < n - 1 - i; ++j) {
				swap(matrix[i][j], matrix[j][n - 1 - i]);
                swap(matrix[i][j], matrix[n - 1 - i][n - 1 - j]);
                swap(matrix[i][j], matrix[n - 1 - j][i]);
            }
        }
    }
};

L49 字母异位词分组

Input: [“eat”, “tea”, “tan”, “ate”, “nat”, “bat”],
Output:
[ [“ate”,“eat”,“tea”],
[“nat”,“tan”],
[“bat”] ]

散列表 + 排序方法

52 ms 19.7 MB

class Solution {
public:
    vector<vector<string>> groupAnagrams(vector<string>& strs) {
        vector<vector<string>> res;
        unordered_map<string, vector<string>> m;
        for (string str : strs) {
            string t = str;
            sort(t.begin(), t.end());
            m[t].push_back(str);
        }
        for (auto a : m) {
            res.push_back(a.second);
        }
        return res;
    }
};

散列表 + 计数方法

164 ms 30.2 MB

class Solution {
public:
    vector<vector<string>> groupAnagrams(vector<string>& strs) {
        vector<vector<string>> res;
        unordered_map<string, vector<string>> m;
        for (string str : strs) {
            vector<int> cnt(26);
            string t;
            for (char c : str) ++cnt[c - 'a'];
            for (int d : cnt) t += to_string(d) + '/';
            // t = '0/2/1/3/4/23/1 .... '
            m[t].push_back(str);
        }
        for (auto a : m) {
            res.push_back(a.second);
        }
        return res;
    }
};

L53 最大子序和

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

暴力

420 ms 9.3 MB TO(n^2); SO(1)

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int maxNum = INT_MIN;
        int numSize = nums.size();
        for (int i = 0; i < numSize; i++)
        {
            int sum = 0;
            for (int j = i; j < numSize; j++)
            {
                sum += nums[j];
                if (sum > maxNum) maxNum = sum;
            }
        }
        return maxNum;
    }
};

DP

4 ms 9.3 MB TO(n) SO(1)

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int dp = nums[0]; // vector dp(numsSize);
        int result = nums[0];
        int numSize = int(nums.size());
        for (int i = 1; i < numSize; i++)
        {
            // dp[i] = max(dp[i - 1] + nums[i], nums[i]);
            dp = max(dp + nums[i], nums[i]);
            result = max(dp, result);
        }
        return result;
    }
};

滑窗方法

O(n)` 思想虽然不一样 但是代码相同

Class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int curSum = 0, res = INT_MIN;
        for (int num : nums)
        {
            curSum = max(curSum + num, num);
            res = max(res, curSum);
        }
        return res;
    }
};

Greedy

8 ms 9.2 MB TO(n) SO(1)

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int result = INT_MIN;
        int numSize = nums.size();
        int sum = 0;
        for (int i = 0; i < numSize; i++)
        {
            sum += nums[i];
            result = max(result, sum);
            if (sum < 0) sum = 0;
        }
        return result;
    }
};

Divide and Conquer Approch

TO(nlgn) SO(lgn)
最大子序要么全在左边 要么全在右边 要么跨中心！

class Solution
{
public:
    int maxSubArray(vector<int> &nums)
    {
        //类似寻找最大最小值的题目，初始值一定要定义成理论上的最小最大值
        int result = INT_MIN;
        int numsSize = int(nums.size());
        result = maxSubArrayHelper(nums, 0, numsSize - 1);
        return result;
    }
    int maxSubArrayHelper(vector<int> &nums, int left, int right)
    {
        if (left == right)
        {
            return nums[left];
        }
        int mid = (left + right) / 2;
        int leftSum = maxSubArrayHelper(nums, left, mid);
        //注意这里应是mid + 1，否则left + 1 = right时，会无线循环
        int rightSum = maxSubArrayHelper(nums, mid + 1, right);
        int midSum = findMaxCrossingSubarray(nums, left, mid, right);
        int result = max(leftSum, rightSum);
        result = max(result, midSum);
        return result;
    }
    int findMaxCrossingSubarray(vector<int> &nums, int left, int mid, int right)
    {
        int leftSum = INT_MIN;
        int sum = 0;
        for (int i = mid; i >= left; i--)
        {
            sum += nums[i];
            leftSum = max(leftSum, sum);
        }
        int rightSum = INT_MIN;
        sum = 0;
        //注意这里i = mid + 1，避免重复用到nums[i]
        for (int i = mid + 1; i <= right; i++)
        {
            sum += nums[i];
            rightSum = max(rightSum, sum);
        }
        return (leftSum + rightSum);
    }
};

L55 跳跃游戏

给定一个非负整数数组，你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个位置。
示例 1:
输入: [2,3,1,1,4]
输出: true
解释: 我们可以先跳 1 步，从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
示例 2:
输入: [3,2,1,0,4]
输出: false
解释: 无论怎样，你总会到达索引为 3

递归穷举

Time Exceeded!
因为这么写，就算true了，还是不能马上结束
因为只能一层层堆栈返回，所以不能递归！

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int n = nums.size() - 1;
        return canJumpDFS(nums, 0, n);
    }
    bool canJumpDFS(vector<int>& nums, int i, int tail) {
        if (tail <= 0) return true;
        if (i >= nums.size()) return false;
        if (nums[i] <= 0) return false;
        for (int k = 1; k <= nums[i]; k++) {
            if (canJumpDFS(nums, i+k, tail-k)) {
                return true;
            }
        }
        return false;
    }
};

动态规划

dp[i] 表示达到i位置时剩余的跳力, 若到达某个位置时跳力为负了，说明无法到达该位置。
dp[i] = max(dp[i - 1], nums[i - 1]) - 1

class Solution {
public:
    bool canJump(vector<int>& nums) {
        vector<int> dp(nums.size(), 0);
        for (int i = 1; i < nums.size(); ++i) {
            dp[i] = max(dp[i-1], nums[i-1]) - 1;
            if (dp[i] < 0) return false;
        }
        return true;
    }
};

贪婪法

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int n = nums.size(), reach = 0; // // 表示最远能到达的位置
        for (int i = 0; i < n; ++i) {
            // 当到不了i或者已经超过数组尾时跳出
            if (i > reach || reach >= n - 1) break;
            // 坐标i可以到达:
            reach = max(reach, i+nums[i]);
        }
        return reach >= n-1;
    }
};

L56 合并区间

给出一个区间的集合，请合并所有重叠的区间

一次排序插入法

如果我们按照区间的 start 大小排序，那么在这个排序的列表中可以合并的区间一定是连续的

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        if (intervals.empty()) return {};
        // 默认对第一列进行排序
        // sort(intervals.begin(), intervals.end());
        sort(intervals.begin(), intervals.end(), // ascend&first-cols
            [](vector<int>&a, vector<int>&b) {return a[0] < b[0];});
        vector<vector<int>> res{intervals[0]};
        for (int i = 0; i < intervals.size(); i++) {
            if (res.back()[1] < intervals[i][0]) {
                res.push_back(intervals[i]);
            }
            else {
                res.back()[1] = max(res.back()[1], intervals[i][1]);
            }
        }
        return res;
    }
};

W2 二次排序方法

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        int n = intervals.size();
        vector<vector<int>> res;
        vector<int> starts, ends;
        for (int i = 0; i < n; ++i) {
            starts.push_back(intervals[i][0]);
            ends.push_back(intervals[i][1]);
        }
        sort(starts.begin(), starts.end());
        sort(ends.begin(), ends.end());
        for (int i = 0, j = 0; i < starts.size(); ++i) {
            if (i == n - 1 || starts[i + 1] > ends[i]) {
                res.push_back({starts[j], ends[i]});
                j = i + 1;  // 出现间隔移动头指针
            }
        }
        return res;
    }
};

W3 来自L57题的所有方法都能用！ _ TODO

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        vector<vector<int>> res;
        for (int i = 0; i < intervals.size(); ++i) {
            res = insert(res, intervals[i]);
        }
        return res;
    }
    vector<vector<int>> insert(vector<vector<int>>& intervals, vector<int> newInterval) {
        vector<vector<int>> res;
        int n = intervals.size(), cur = 0;
        for (int i = 0; i < n; ++i) {
            if (intervals[i][1] < newInterval[0]) {
                res.push_back(intervals[i]);
                ++cur;
            } else if (intervals[i][0] > newInterval[1]) {
                res.push_back(intervals[i]);
            } else {
                newInterval[0] = min(newInterval[0], intervals[i][0]);
                newInterval[1] = max(newInterval[1], intervals[i][1]);
            }
        }
        res.insert(res.begin() + cur, newInterval);
        return res;
    }
};

L62 不同路径

一个机器人位于一个$m\times n$网格的左上角 （起始点在下图中标记为“Start” ）机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。
问总共有多少条不同的路径？

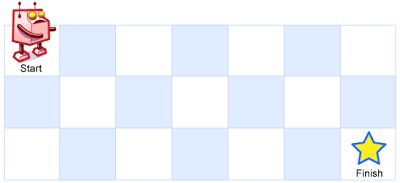
数学排列组合

class Solution {
public:
    int uniquePaths(int m, int n) {
        // C(min(m - 1, n - 1), m + n - 2)
        int S = m + n - 2;
        double res = 1;
        for (int i = 1; i <= min(m, n) - 1; i++) {
            res *= S--;
            res /= i;
        }
        return int(res);
    }
};

DP

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<int> dp(n, 1);
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                dp[j] += dp[j - 1];  // 按行刷新！
            }
        }
        return dp[n - 1];
    }
};

W3 不设动态规划数组+原地累加

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        if (grid.empty()) return 0;
        for (int i = 0; i < grid.size(); i++) {
            for (int j = 0; j < grid[0].size(); ++j) {
                if (i == 0 && j == 0) continue;
                else if (i == 0) grid[i][j] += grid[i][j-1];
                else if (j == 0) grid[i][j] += grid[i-1][j];
                else grid[i][j] += min(grid[i-1][j],grid[i][j-1]);
            }
        }
        return grid.back().back();
    }
};

W4 = W3

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        if (grid.empty() || grid[0].empty()) return 0;
        for (int i = 0; i < grid.size(); ++i) {
            for (int j = 0; j < grid[i].size(); ++j) {
                if (i == 0 && j == 0) continue;
                int up = (i == 0) ? INT_MAX : grid[i - 1][j];
                int left = (j == 0) ? INT_MAX : grid[i][j - 1];
                grid[i][j] += min(up, left);
            }
        }
        return grid.back().back();
    }
};

L64 最小路径和

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

动态规划

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        if (grid.empty()) return 0;
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> dp(m, vector<int>(n));
        //原点
        dp[0][0] = grid[0][0];
        //第一列只从上来
        for (int i = 1; i < m; i++) dp[i][0] = grid[i][0] + dp[i-1][0];
        //第一行只从右来
        for (int j = 1; j < n; j++) dp[0][j] = grid[0][j] + dp[0][j-1];
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                dp[i][j] = min(dp[i-1][j], dp[i][j-1])+grid[i][j];
            }
        }
        return dp[m-1][n-1];
    }
};

一维动态规划方法

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        if (grid.empty()) return 0;
        int m = grid.size(), n = grid[0].size();
        vector<int> dp(n, INT_MAX);
        dp[0] = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (j == 0) dp[j] += grid[i][j]; // 第一行
                else dp[j] = grid[i][j] + min(dp[j], dp[j-1]);
            }
        }
        return dp[n-1];
    }
};

L70 爬楼梯

假设你正在爬楼梯。需要n阶你才能到达楼顶, 每次你可以爬1或2个台阶
问多少种方法！

动态规划

class Solution {
public:
    int climbStairs(int n) {
        int a = 1, b = 2, c;
        while (n > 2)
        {
            c = a + b;   
            a = b; b = c;            
            --n;
        }
        return c;
    }
};

递归

class Solution {
public:
    int climbStairs(int n) {
        vector<int> memo(n + 1);
        return helper(n, memo);
    }
    int helper(int n, vector<int>& memo)
    {
        if (n <= 2) return n;
        if (memo[n] > 0) return memo[n];
        return memo[n] = helper(n - 1, memo) + 
        				 helper(n - 2, memo);
    }
};

分治

分情况，将楼梯分为上半部和下半部，
按两个部分是按照1步还是2步相连的情况分为两种情况！
1步联系(n/2,n-n/2), 2步联系(n/2-1,n-n/2-1)

class Solution {
public:
    int climbStairs(int n) {
        if(n <= 3) return n;       
        return climbStairs(n / 2) * climbStairs(n - n / 2) + 
            climbStairs(n / 2 - 1) * climbStairs(n - n / 2 - 1);
    }
};

斐波拉契数列通项公式

class Solution {
public:
    int climbStairs(int n) {
        double root5 = sqrt(5);
        return (1 / root5) * (pow((1 + root5) / 2, n + 1) - 
                              pow((1 - root5) / 2, n + 1));
    }
};

L72 编辑距离

给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作：
插入一个字符
删除一个字符
替换一个字符

递归搜索

下面的程序时对的，但是过不了OJ，因为会重复判断很多情况(三层递归)

class Solution {
public:
    int minDistance(string word1, string word2) {
        // int m = word1.size(), n = word2.size();
        return countFunc(word1, 0, word2, 0);
    }
    int countFunc(string& w1, int i, string& w2, int j) {
        if (i == w1.size()) return (int)w2.size() - j;
        if (j == w2.size()) return (int)w1.size() - i;
        int res = 0;
        if (w1[i] == w2[j]) return countFunc(w1, i+1, w2, j+1);
        else {
            int ins_cnt = countFunc(w1, i, w2, j+1);
            int del_cnt = countFunc(w1, i+1, w2, j);
            int mod_cnt = countFunc(w1, i+1, w2, j+1);
            res = min(min(ins_cnt, del_cnt), mod_cnt) + 1;
        }
        return res;
    }
};

递归+备忘录

记忆数组memo会记录下已经访问到的情况，避免重复访问！
时间换空间

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.size(), n = word2.size();
        vector<vector<int>> memo(m, vector<int>(n, 0));
        return countFunc(word1, 0, word2, 0, memo);
    }
    int countFunc(string& w1, int i, string& w2, int j, 
                    vector<vector<int>>& memo) {
        // 其中1个数组已经访问完毕
        if (i == w1.size()) return (int)w2.size() - j;
        if (j == w2.size()) return (int)w1.size() - i;
        // 当前情况之前已经被访问
        if (memo[i][j] > 0) return memo[i][j];
        // 比较+三种操作(插入/删除/修改)
        if (w1[i] == w2[j]) return countFunc(w1, i+1, w2, j+1, memo);
        else {
            int ins_cnt = countFunc(w1, i, w2, j+1, memo);
            int del_cnt = countFunc(w1, i+1, w2, j, memo);
            int mod_cnt = countFunc(w1, i+1, w2, j+1, memo);
            memo[i][j] = min(min(ins_cnt, del_cnt), mod_cnt) + 1;
        }
        return memo[i][j];
    }
};

动态规划

注意边界和动态数组的大小
PS: 上个方法的memo和这里的DP异曲同工！

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.size(), n = word2.size();
        vector<vector<int>> dp(m+1, vector<int>(n+1));
        for (int i = 0; i <= m; i++) dp[i][0] = i; // DP边界
        for (int j = 0; j <= n; j++) dp[0][j] = j;
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (word1[i-1] == word2[j-1]) {
                    dp[i][j] = dp[i-1][j-1];
                }           
                else {
                    dp[i][j] = min(min(dp[i][j-1], 
                        dp[i-1][j]), dp[i-1][j-1]) + 1;
                }

            }
        }
        return dp.back().back();
    }
};

L75 颜色分类

给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，
使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。
此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

• In-plane?
• 一边遍历

计数重写法

class Solution {
public:
    void sortColors(vector<int>& nums) {
        vector<int> colors(3); int index = 0;
        for (int num : nums) ++colors[num];
        while(colors[0]--) nums[index++] = 0;
        while(colors[1]--) nums[index++] = 1;
        while(colors[2]--) nums[index++] = 2;
    }
};

One-pass方法

• 三指针
• 分别表示0色的最右边界，2色的最左边界，当前颜色的位置！
• 双指针框架

class Solution {
public:
    void sortColors(vector<int>& nums) {
        int left = 0, right = nums.size() - 1;
        for (int cur = 0; cur <= right; cur++) {
            if (nums[cur] == 2) swap(nums[cur--], nums[right--]);
            else if (nums[cur] == 0) swap(nums[left++], nums[cur]);
        }
    }
};

L76 最小覆盖子串

给你一个字符串 S、一个字符串 T，请在字符串 S 里面找出：包含 T 所有字母的最小子串。
示例：
输入: S = “ADOBECODEBANC”, T = “ABC”
输出: “BANC”
说明：
如果 S 中不存这样的子串，则返回空字符串 “”。
如果 S 中存在这样的子串，我们保证它是唯一的答案。

滑动窗

• 难点有二：① 滑动窗的设置：$--label[s[right]]>=0和win$ ② return的选择
• label也可以换成unordered_map

class Solution {
public:
    string minWindow(string s, string t) {
        vector<int> label(128,0);
        for (auto& c : t) label[c]++;
        int left = 0, right = 0;
        int start = -1, len = INT_MAX;
        int win = 0;
        while (right < s.size()) {
            if (--label[s[right]] >= 0) win++;
            right++;
            while (win == t.size()) {
                if (len > right - left) {
                    len = right - left;
                    start = left;
                }
                if (++label[s[left]] > 0) win--;
                left++;
            }
        }
        return start == -1 ? "" : s.substr(start, len);
    }
};

L78 子集

• 给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。
  说明：解集不能包含重复的子集。
  输入: nums = [1,2,3]
  输出:
  $$[[3],[1],[2],[1,2,3],[1,3],[2,3],[1,2],[]]$$

迭代方法

往上叠加
输出：
[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        if (nums.size() < 1) return vector<vector<int>>();
        vector<vector<int>> res;
        res.push_back({}); // []
        sort(nums.begin(), nums.end());
        for (int i = 0; i < nums.size(); ++i) {
            int S = res.size(); // 这里一定要要 
            // 下面这个循环的res长度是变化的
            for (int j = 0; j < S; ++j) {
                res.push_back(res[j]);
                res.back().push_back(nums[i]);
            }
        }
        return res;
    }
};

递归方法(数归)

• 输出 $[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]$

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        if (nums.empty()) return {{}};
        int n = nums.back();
        nums.pop_back();
        vector<vector<int>> res = subsets(nums);
        int N = res.size(); // res循环中会变长 所有长度要先提出来
        for (int i = 0; i < N; ++i) {
            res.push_back(res[i]);
            res.back().push_back(n);
        }
        return res;
    }
};

回溯

输出：$[[],[1],[1,2],[1,2,3],[1,3],[2],[2,3],[3]]$

class Solution {
public:
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        vector<vector<int>> res;
        vector<int> track;
        sort(nums.begin(), nums.end()); // 不同1
        backtrack(res, nums, track, 0);
        return res;
    }
    void backtrack(vector<vector<int>>& res,vector<int>& nums,vector<int>& track,int pos) {
        res.push_back(track);
        for (int i = pos; i < nums.size(); ++i) {
            track.push_back(nums[i]);
            backtrack(res,nums,track,i+1);
            track.pop_back();
            while (i+1 < nums.size()&&nums[i]==nums[i+1]) i++; // 不同2
        }
    }
};

W3 CC
TODO 有时间再研究

	1	2	3	Subset
0	F	F	F	[]
1	F	F	T	3
2	F	T	F	2
3	F	T	T	23
4	T	F	F	1
5	T	F	T	13
6	T	T	F	12
7	T	T	T	123

class Solution {
public:
    vector<vector<int> > subsets(vector<int> &S) {
        vector<vector<int> > res;
        sort(S.begin(), S.end());
        int max = 1 << S.size();
        for (int k = 0; k < max; ++k) {
            vector<int> out = convertIntToSet(S, k);
            res.push_back(out);
        }
        return res;
    }
    vector<int> convertIntToSet(vector<int> &S, int k) {
        vector<int> sub;
        int idx = 0;
        for (int i = k; i > 0; i >>= 1) {
            if ((i & 1) == 1) {
                sub.push_back(S[idx]);
            }
            ++idx;
        }
        return sub;
    }
};

L79 单词搜索

给定一个二维网格和一个单词，找出该单词是否存在于网格中。
单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格只能上下左右，走迷宫！。同一个单元格内的字母不允许被重复使用。
board =
$$\begin{gathered} [{[}^{\prime }{A}^{\prime }{,}^{\prime }{B}^{\prime }{,}^{\prime }{C}^{\prime }{,}^{\prime }{E}^{\prime }], \\ {[}^{\prime }{S}^{\prime }{,}^{\prime }{F}^{\prime }{,}^{\prime }{C}^{\prime }{,}^{\prime }{S}^{\prime }], \\ {[}^{\prime }{A}^{\prime }{,}^{\prime }{D}^{\prime }{,}^{\prime }{E}^{\prime }{,}^{\prime }{E}^{\prime }]] \end{gathered}$$
给定 word = “ABCCED”, 返回 true.
给定 word = “SEE”, 返回 true.
给定 word = “ABCB”, 返回 false.

回溯

W1 DFS + 标记数组

class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {
        int ht = board.size(), wd = board[0].size();
        vector<vector<bool>> v(ht, vector<bool>(wd, false));
        for (int i = 0; i < ht; i++) {
            for (int j = 0; j < wd; j++) {
                if (backtrack(board,word,v,0,i,j)) 
                    return true;
            }
        }
        return false;
    }
    bool backtrack(vector<vector<char>>& b, string& w, 
        vector<vector<bool>>& v, int inx, int i, int j) {
        int ht = b.size(), wd = b[0].size();
        if (inx == w.size()) return true;
        if (i < 0 || j < 0 || i >= ht || j >= wd) return false;
        if (v[i][j] || b[i][j] != w[inx]) return false;
        v[i][j] = true;
        bool res = backtrack(b,w,v,inx+1,i+1,j) || 
                   backtrack(b,w,v,inx+1,i-1,j) || 
                   backtrack(b,w,v,inx+1,i,j+1) || 
                   backtrack(b,w,v,inx+1,i,j-1);
        v[i][j] = false;
        return res;
    }
};

W2 DFS + 原地标记
使用#替代原数组已表示访问到了，当回溯的时候记得恢复！

class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {
        if (board.size() < 1) return false;
        int h = board.size(), w = board[0].size();
        for (int y = 0; y < h; ++y) {
            for (int x = 0; x < w; ++x) {
                if (searchDFS(board, word, 0, x, y))
                    return true;
            }
        }
        return false;
    }
    bool searchDFS(vector<vector<char>>& board, string word, 
            int index, int x, int y) {
        if (index == word.size()) return true; // 剪枝
        int h = board.size(), w = board[0].size();
        if (x < 0 || y < 0 || x >= w || y >= h // 剪枝
            || board[y][x] != word[index]) return false;
        char tmp = board[y][x];
        board[y][x] = '#';
        bool res = searchDFS(board, word, index+1, x-1, y) ||
            searchDFS(board, word, index+1, x+1, y) ||
            searchDFS(board, word, index+1, x, y-1) ||
            searchDFS(board, word, index+1, x, y+1);
        board[y][x] = tmp;
        return res;
    }
};

L84 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。

穷举方法

穷举所有可能的左边界，按照规则找最大的矩形面积！
过不了OJ，时间复杂度是N^2！

class Solution {
public:
    int largestRectangleArea(vector<int> &height) {
        int res = 0;
        for (int i = 0; i < height.size(); ++i) {
            int min_h = height[i];
            int s_res = min_h;
            for (int j = i; j < height.size(); ++j) {
                min_h = min(min_h, height[j]);
                s_res = (s_res > min_h*(j-i+1)) ? s_res : min_h*(j-i+1);
            }
            res = (res > s_res) ? res : s_res;
        }
        return res;
    }
};

滑动窗

• 滑动窗扩大，右移右边界到降序点
• 滑动窗缩小，从右边界往左找最小高度
• 不足：当滑动窗缩小的时候，左边界从右往左搜索最小高度时候，出现“凹”情况的时候，是没必要再继续往左搜索了，所以单调栈后序会改进这部分，使得复杂度进一步降低！

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        if (heights.empty()) return 0;
        int left = 0, right = 0;
        int res = heights[0];
        while (right < heights.size()) {
            right++; // 滑动窗扩大
            int labelHt = right < heights.size() ? heights[right] : INT_MIN;
            int minHt = heights[right - 1]; // 最小高度
            left = right - 1;
            while (left >= 0 && labelHt < heights[right - 1]) { 
                // 滑动窗缩小(特殊的是从右往左移动左边界)
                minHt = min(heights[left], minHt); // 最小高度！
                int area = (right-left) * minHt;
                res = max(res, area);
                left--;
            }
        }
        return res;
    }
};

单调栈

• Monotone Stack 单调栈

• 栈中元素按照单调性递减(如单增时从栈底算，从小到大排列)，可存坐标

• 元素只能进栈一次，出栈之后就不能在进栈了，线性的时间复杂度

• 单调栈分为单调递增栈和单调递减栈

• • 单调递增栈即栈内元素保持单调递增的栈
• • 同理单调递减栈即栈内元素保持单调递减的栈

• 操作规则（下面都以单调递增栈为例）

• • 如果新的元素比栈顶元素大，就入栈
• • 如果新的元素较小，那就一直把栈内元素弹出来，直到栈顶比新元素小

• 加入这样一个规则之后，会有什么效果

• • 栈内的元素是递增的
• • 当元素出栈时，说明这个新元素是出栈元素向后找第一个比其小的元素
• • 同理，单减栈元素出栈的时候，说明新元素是出栈元素向后找第一个比其大的元素

• 该题的模拟流程：可以看出处理完栈非空，所以可以在height后面加一个"0"元素的尾巴，让栈再循环中情况！

• 该题为单增栈！
  

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int maxR = 0;
        stack<int> st;
        heights.push_back(0);
        for (int i = 0; i < heights.size(); i++) {
            while (!st.empty() && heights[i] <= heights[st.top()]) {
                auto x = st.top(); st.pop();
                int area = heights[x] * (st.empty() ? i : i - st.top() - 1);
                maxR = max(maxR, area);
            }
            st.push(i);
        }
        return maxR;
    }
};

L85 最大矩形

给定一个仅包含 0 和 1 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。
输入:
$$\begin{gathered} [["1","0","1","0","0"], \\ ["1","0","1","1","1"], \\ ["1","1","1","1","1"], \\ ["1","0","0","1","0"]] \end{gathered}$$
输出: 6

单调栈

从矩阵的最后一行开始，记录每行的处在最长bin的高度
再使用84题得到每行的最大矩形框的全局最大值！

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        if (matrix.empty()) return 0;
        int ht = matrix.size(), wd = matrix[0].size();
        vector<vector<int>> M(ht,vector<int>(wd,0));
        for (int i = 0; i < ht; i++)
            for (int j = 0; j < wd; j++)
                if (matrix[i][j] == '1')
                    M[i][j] = i > 0 ? M[i-1][j] + 1 : 1;
        int maxH = 0;
        for (int i = 0; i < ht; i++) 
            maxH = max(maxH, maxRect1D(M[i]));
        return maxH;
    }
    int maxRect1D(vector<int>& ht) {
        int maxH = 0;
        stack<int> st;
        ht.push_back(0);
        for (int i = 0; i < ht.size(); i++) {
            while (!st.empty() && ht[st.top()] >= ht[i]) {
                int x = st.top(); st.pop();
                int area = (st.empty()?i:i-st.top()-1) * ht[x];
                maxH = max(maxH, area);
            }
            st.push(i);
        }
        return maxH;
    }
};

动态规划

S(M) T(MN) ：每行M迭代N次
包括有高度、左边界、右边界和面积的四个递推公式！

直觉
想象一个算法，对于每个点我们会通过以下步骤计算一个矩形：
1 不断向上方遍历，直到遇到“0”，以此找到矩形的最大高度。
2 向左右两边扩展，直到无法容纳矩形最大高度。

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        if (matrix.size() == 0) return 0;
        int h = matrix.size(), w = matrix[0].size();
        vector<int> ht(w, 0), lb(w, 0), rb(w, w);
        int res = 0;
        for (int j = 0; j < h; ++j) {
            int cur_left = 0, cur_right = w;
            for (int i = 0; i < w; ++i) {
                if (matrix[j][i] == '1') ++ht[i];
                else ht[i] = 0;
            }
            for (int i = 0; i < w; ++i) {
                if (matrix[j][i] == '1') lb[i] = max(cur_left, lb[i]);
                else {lb[i] = 0; cur_left = i+1;}              
            }
            for (int i = w-1; i >= 0; --i) {
                if (matrix[j][i] == '1') rb[i] = min(cur_right, rb[i]);
                else {rb[i] = w; cur_right = i;}              
            }
            for (int i = 0; i < w; ++i) {
                res = max(res, ht[i] * (rb[i] - lb[i]));
            }
        }
        return res;
    }
};

L94 二叉树的中序遍历

• 返回二叉树的中序遍历!

中序递归遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        inOrder(root, res);
        return res;
    }
    void inOrder(TreeNode* root, vector<int>& res) {
        if (!root) return;
        inOrder(root->left, res);
        res.push_back(root->val);
        inOrder(root->right, res);
    }
};

中序迭代遍历

载入完左节点，再载入右节点

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> s;
        TreeNode* p = root;
        while (p || !s.empty()) {
            while (p) {
                s.push(p);
                p = p->left;
            }
            p = s.top(); s.pop();
            res.push_back(p->val);
            p = p->right;            
            // if (p) {
            //     s.push(p);
            //     p = p->left;
            // }
            // else {
            //     p = s.top(); s.pop();
            //     res.push_back(p->val);
            //     p = p->right;
            // }
        }
        return res;
    }
};

Morris Traversal

不需要栈的迭代遍历方法

---

数据结构知识记录:
Threaded binary tree

• 线索二叉树
• 去除空指针，空指针没有充分利用
• 利用那些空地址，存放指向结点在某次遍历次序下的前驱和后继结点的地址 > 双向链表
• 把对二叉树以某种次序遍历使其变为线索二叉树的过程称做是线索化
• 二叉树进行中序遍历后，将所有的空指针域中的rchild，改为指向它的后继结点
• 二叉树进行中序遍历后，将所有的空指针域中的lchild，改为指向它的前驱结点
  
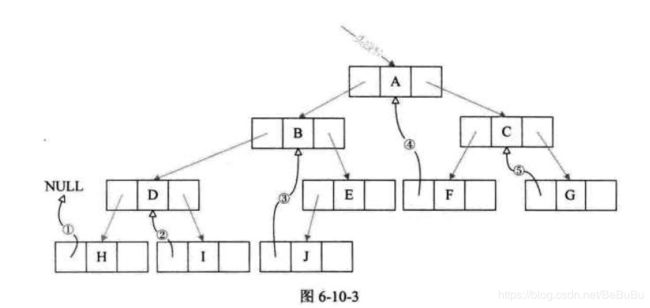
  得到一个‘双向链表’
  
• 线索二叉树充分利用了空指针域的空间，又保证了创建时一次遍历就可以持续受用的前驱后继信息，所以如果所用的二叉树需要经常遍历或查找结点时需要某种遍历序列中的前驱后继，那么采用线索二叉链表的存储结构就是不错的选择
• 为了区分指针域是指向左右孩子还是前驱后继，需要再增加两个标志位ltag和rtag，ltag为0时表示指向左孩子，为1时表示指向前驱，rtag为0时表示指向右孩子，为1时表示指向后继。
  

---

这是Morris方法解决中序遍历的思路：

class Solution {
public:
    vector<int> inorderTraversal(TreeNode *root) {
        vector<int> res;
        if (!root) return res;
        TreeNode *cur, *pre;
        cur = root;
        while (cur) {
            if (!cur->left) { // 插入
                res.push_back(cur->val);
                cur = cur->right;
            } else { // 建立线索
                pre = cur->left;
                while (pre->right && pre->right != cur) pre = pre->right;
                if (!pre->right) {
                    pre->right = cur;
                    cur = cur->left;
                } else {
                    pre->right = NULL;
                    res.push_back(cur->val);
                    cur = cur->right;
                }
            }
        }
        return res;
    }
};

• 二叉树的三种常见遍历顺序(先序，中序，后序)就有三种解法(递归，非递归，Morris 遍历)，总共有九段代码！二叉树的层序遍历也有递归和非递归解法。

L96 不同的二叉搜索树

节点数为n的不同BST有多少？

Catalan数

• 问题描述：12个高矮不同的人，排成两排，每排必须是从矮到高排列，而且第二排比对应的第一排的人高，问排列方式有多少种？
• 我们先把这12个人从低到高排列,然后,选择6个人排在第一排,那么剩下的6个肯定是在第二排. 用0表示对应的人在第一排,用1表示对应的人在第二排,
• 问题转换为，这样的满足条件的01序列有多少个。观察1的出现，我们考虑这一个出现能不能放在第二排，显然，在这个1之前出现的那些0,1对应的人要么是在这个1左边，要么是在这个1前面。而肯定要有一个0的，在这个1前面，统计在这个1之前的0和1的个数。也就是要求，合法序列要求：0的个数大于1的个数 或者叫合法的入栈出栈序列有多少种！（把0看成入栈操作，1看成出栈操作，即0的累计个数不小于1的排列有多少种）
• 递推关系推导：合法入栈出栈序列个数角度，怎么解释这个$k$呢,因为这个$k$是最后出栈的,因此当$k$入栈时$1到k-1$已经全部出栈了,也就是前$k-1$个数有$f(k-1)$种序列,而当$k$出栈时$k+1到n$已经全部出栈了,也就是后$n-k$个数有$f(n-k)$种序列,根据乘法原理,当最后一个数为$k$时,$f(n)=f(k-1)\times f(n-k)$,再根据加法原理,$k=1,2,...n$,即为$f(n)=h(n)=C(2n,n)/(n+1)=c(2n,n)-c(2n,n+1);(n=0，1，2，\dots \dots )$。

---

Catalan数 下列关系等价

• $f(n)=\frac{C_{2n}^n}{n+1}$ > 通项1
• $f(n)=C_{2n}^n-C_{2n}^{n-1}$ > 通项2
• $f(n)={\sum }_{i=0}^{n-1}f(i)\times f(n-i-1)$ > 递推

这道题使用Catalan的递推公式去理解$f(n)={\sum }_{i=0}^{n-1}f(i)\times f(n-i-1)$
W1 DP
$C_0=1$ and $C_{n+1}={\sum }_{i=0}^n{C}_i{C}_{n-i}$ for $n\ge 0$

class Solution {
public:
    int numTrees(int n) {
        vector<int> res(n+1, 0); // 算上空树 所以是n+1
        res[0] = 1;
        for (int i = 1; i <= n; ++i) {
            for (int j = 0; j < i; ++j) {
                res[i] += res[j] * res[i - j - 1];
            }
        }
        return res.back();
    }
};

W2 通项
$f(n)=\frac{C_{2n}^n}{n+1}$

class Solution {
public:
    int numTrees(int n) {
        long res = 1;
        for (int i = n + 1; i <= 2 * n; ++i) {
            res = res * i / (i - n);
        }
        return res / (n + 1);
    }
};

L98 验证二叉搜索树

左<中<右
注意：一般还有BST定义成左<=中<右

递归

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        return judge(root, LONG_MIN, LONG_MAX);
    }
    bool judge(TreeNode* root, long mn, long mx) {
        if (!root) return true;
        if (root->val <= mn || root->val >= mx) return false;
        return judge(root->left, mn, root->val) && 
                judge(root->right, root->val, mx);
    }
};

中序遍历

一般对于BST定义成左<=中<右的情况，20 - 20这种情况，中序遍历做不了

   20       20
   /         \
 20 (是BST)   20(不是BST)

而原题改为左<中<右，所以可以用中序便离开了做？
遍历成列表，插入列表，看是不是升序！

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        TreeNode *pre = NULL;
        return inorder(root, pre);
    }
    bool inorder(TreeNode* root, TreeNode*& pre) {
        if (!root) return true;
        bool res = inorder(root->left, pre);
        if (!res) return false;
        if ( pre && root->val <= pre->val) 
            return false;
        pre = root;
        return inorder(root->right, pre);
    }
};

栈 - 迭代 - 中序

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        stack<TreeNode*> s;
        TreeNode *p = root, *pre = NULL;
        while (p || !s.empty()) {
            while (p) {
                s.push(p);
                p = p->left;
            }
            p = s.top(); s.pop();
            if (pre && p->val <= pre->val) return false;
            pre = p;
            p = p->right;
        }
        return true;
    }
};

Morris - 中序

class Solution {
public:
    bool isValidBST(TreeNode *root) {
        if (!root) return true;
        TreeNode *cur = root, *pre, *parent = NULL;
        bool res = true;
        while (cur) {
            if (!cur->left) {
                if (parent && parent->val >= cur->val) res = false;
                parent = cur;
                cur = cur->right;
            } else {
                pre = cur->left;
                while (pre->right && pre->right != cur) pre = pre->right;
                if (!pre->right) {
                    pre->right = cur;
                    cur = cur->left;
                } else {
                    pre->right = NULL;
                    if (parent->val >= cur->val) res = false;
                    parent = cur;
                    cur = cur->right;
                }
            }
        }
        return res;
    }
};

L101 对称二叉树

给定一个二叉树，检查它是否是镜像对称的。

递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (!root) return true;
        return isSymSubTree(root->left, root->right);
    }
    bool isSymSubTree(TreeNode* left, TreeNode* right)
    {
        if (!left && !right) return true;
        if (left && !right || !left && right || 
        	left->val != right->val) return false;
        return isSymSubTree(left->left, right->right) && 
            isSymSubTree(left->right, right->left);
    }
};

迭代

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (!root) return true;
        queue<TreeNode*> q1, q2;
        q1.push(root->left);
        q2.push(root->right);
        while (!q1.empty() && !q2.empty())
        {
            TreeNode *node1 = q1.front(); q1.pop();
            TreeNode *node2 = q2.front(); q2.pop();
            // 1存在NULL节点 迭代不像递归可以直接return-true 
            // 2递归的return是存在一个false就false 这里的false是唯一的不能直接return
            // 3因为我们还没有比较完，有可能某个结点没有左子结点，但是右子结点仍然存在，所以这里只能continue
            if (!node1 && !node2) continue; 
            if ((!node1 && node2) || (node1 && !node2)) return false;
            if (node1->val != node2->val) return false;
            q1.push(node1->left);
            q1.push(node1->right);
            q2.push(node2->right);
            q2.push(node2->left);
        }
        return true;
    }
};

L102 二叉树的层序遍历

迭代

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> res;
        if (!root) return res;
        queue<TreeNode*> que; // que({root})
        que.push(root);
        while (!que.empty()) {
            vector<int> level;
            for (int i = que.size(); i > 0; --i) { 
                // PS:q在循环中会变长
                TreeNode *t = que.front();que.pop();
                level.push_back(t->val);
                if (t->left) que.push(t->left);
                if (t->right) que.push(t->right);
            }
            res.push_back(level);
        }
        return res;
    }
};

递归

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> res;
        levelInsertDFS(root, 0, res);
        return res;
    }
    void levelInsertDFS(TreeNode* node, int level, vector<vector<int>>& res) {
        if (!node) return;
        if (res.size() == level) res.push_back({});
        res[level].push_back(node->val);
        if (node->left) levelInsertDFS(node->left,level+1,res);
        if (node->right) levelInsertDFS(node->right,level+1,res);
    }
};

L104 二叉树的最大深度

DFS

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (!root) return 0;
        return 1 + max(maxDepth(root->left), 
               maxDepth(root->right));
    }
};

BFS

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (!root) return 0;
        int res = 0;
        queue<TreeNode*> q({root}); // 先进先出
        while (!q.empty())
        {
            ++res;
            for (int i = q.size(); i > 0; --i)
            { // 注for(int i = 0; i < q.size(); ++i)会报错
              // int i = q.size()是初始化 同for下是二叉树的同层
                TreeNode *t = q.front(); q.pop();
                if (t->left) q.push(t->left);
                if (t->right) q.push(t->right);
            }
        }
        return res;
    }
};

L105 从前序与中序遍历序列构造二叉树

• 前中或后中可以恢复二叉树
• 前后无法恢复，如AB，不知道不知道B是A的左节点还是右节点！
• 记住 遍历的特点：如：左-中-右是中序遍历，中左右是前序遍历，然后数组划分即可！

class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        return buildTree(preorder,0,preorder.size()-1,inorder,0,inorder.size()-1);
    }
    TreeNode* buildTree(vector<int>& preorder,int pl,int pr,
                        vector<int>& inorder,int il,int ir) {
        if (pl > pr || il > ir) return NULL;
        int k = 0; // root idx
        for (k = il; k <= ir; ++k) {
            if (preorder[pl] == inorder[k]) break;
        }
        TreeNode *cur = new TreeNode(preorder[pl]);
        cur->left = buildTree(preorder,pl+1,pl+k-il,inorder,il,k-1);
        cur->right = buildTree(preorder,pl+k-il+1,pr,inorder,k+1,ir);
        return cur;
    }
};

L114 二叉树展开为链表

in-plane

    1
   / \
  2   5
 / \   \
3   4   6
=> 1-2-3-4-5-6

递归 - 先序

     1
    / \
   2   5
  / \   \
 3   4   6
 =>
      1
       \
         2       5
          \       \
            3   4   6

class Solution {
public:
    void flatten(TreeNode* root) {
        stack<TreeNode*> sk;
        dfs_helper(root, sk);
    }
    void dfs_helper(TreeNode*& node, stack<TreeNode*>& sk) {
        if (!node) return;
        if (node->left) { // 将右子树压下栈 将左子树移到右子树
            sk.push(node->right);
            node->right = node->left;
            node->left = NULL;
        }
        dfs_helper(node->right, sk);
        while (!sk.empty()) { // 将栈中元素接到链表上
            node->right = sk.top(); sk.pop();
            dfs_helper(node->right, sk);
        }
    }
};

递归 - 后序

     1
    / \
   2   5
  / \   \
 3   4   6

     1
    / \
   2   5
    \   \
     3   6
      \    
       4

   1
    \
     2
      \
       3
        \
         4
          \
           5
            \
             6

class Solution {
public:
    void flatten(TreeNode* root) {
        if (!root) return;
        if (root->left) flatten(root->left);
        if (root->right) flatten(root->right);
        TreeNode* tmp = root->right;
        root->right = root->left;
        root->left = NULL;
        while (root->right) root = root->right;
        root->right = tmp;
    }
};

迭代

从根节点开始出发，先检测其左子结点是否存在，如存在则将根节点和其右子节点断开，将左子结点及其后面所有结构一起连到原右子节点的位置，把原右子节点连到元左子结点最后面的右子节点之后。

     1
    / \
   2   5
  / \   \
 3   4   6

   1
    \
     2
    / \
   3   4
        \
         5
          \
           6
           
   1
    \
     2
      \
       3
        \
         4
          \
           5
            \
             6

class Solution {
public:
    void flatten(TreeNode* root) {
        TreeNode *cur = root;
        while (cur) {
            if (cur->left) {
                TreeNode* tmp = cur->left;
                while (tmp->right) tmp = tmp->right; 
                tmp->right = cur->right; // 左尾接右头
                cur->right = cur->left;  // 左头右移
                cur->left = NULL;
            }
            else {
                cur = cur->right;
            }
        }
    }
};

W4 前序迭代

class Solution {
public:
    void flatten(TreeNode* root) {
        if (!root) return;
        stack<TreeNode*> st;
        st.push(root);
        while (!st.empty()) {
            TreeNode *t = st.top(); st.pop();
            if (t->left) {
                TreeNode *r = t->left;
                while (r->right) r = r->right;
                r->right = t->right;
                t->right = t->left;
                t->left = NULL;
            }
            if (t->right) st.push(t->right);
        }
    }
};

L121 买卖股票的最佳时机

输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，
在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int minNum = INT_MAX;
        int maxDelta = 0;
        for (int price : prices)
        {
            minNum = min(minNum, price);
            maxDelta = max(maxDelta, price - minNum);
        }
        return maxDelta;
    }
};

L124 二叉树中的最大路径和

1 给定一个非空二叉树，返回其最大路径和。
2 本题中，路径被定义为一条从树中任意节点出发，达到任意节点的序列。该路径至少包含一个节点，且不一定经过根节点。
对于每个结点来说，要知道经过其左子结点的 path 之和大还是经过右子节点的 path 之和大。递归函数返回值就可以定义为以当前结点为根结点，到叶节点的最大路径之和，然后全局路径最大值放在参数中，用结果 res 来表示。

class Solution {
public:
    int maxPathSum(TreeNode* root) {
        int res = INT_MIN;
        dfs_helper(root, res);
        return res;
    }
    int dfs_helper(TreeNode* node, int& res) {
        if (!node) return 0;
        int left = max(dfs_helper(node->left,res),0);
        int right = max(dfs_helper(node->right,res),0);
        res = max(res,left+right+node->val);
        return max(left,right)+node->val;
    }
};

返回最大路径的代码怎么写？

L128 最长连续序列

给定一个未排序的整数数组，找出最长连续序列的长度。
要求算法的时间复杂度为 O(n)。

W1 Hashset

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        int res = 0;
        unordered_set<int> s(nums.begin(), nums.end());
        for (int val : nums) {
            if (!s.count(val)) continue;
            s.erase(val);
            int pre = val - 1;
            int nex = val + 1;
            while (s.count(pre)) s.erase(pre--); // 连续数字会自动擦除
            while (s.count(nex)) s.erase(nex++); // 连续数组擦除
            res = max(res, nex - pre - 1);
        }
        return res;
    }
};

W2 Hashmap

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        int res = 0;
        unordered_map<int,int> m;
        for (int num : nums) {
            if (m.count(num)) continue; 
            int left = m.count(num-1)? m[num-1] : 0;  // 左距
            int right = m.count(num+1)? m[num+1] : 0; // 右距
            int sum = left + right + 1;
            m[num] = sum;
            res = max(res, sum);
            m[num-left] = sum;
            m[num+right] = sum;
        }
        return res;
    }
};

L136 只出现一次的数字

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

W0 HashSet

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        unordered_set<int> st; // HashSet
        for (int num : nums)
        {
            if (st.count(num)) st.erase(num);
            else st.insert(num);
        }
        return *st.begin(); // *解引用可解迭代器
    }
};

W1 Bit Operation

位运算特殊性质

交换律：a ^ b ^ c <=> a ^ c ^ b
任何数于0异或为任何数 0 ^ n => n
相同的数异或为0: n ^ n => 0

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        // 0与0 '异或' 是0，1与1 '异或' 也是0
        int res = 0;
        for (auto num : nums) res ^= num;
        return res;
    }
};

L139 单词拆分

字符串拆分
解题的两大神器: 使用记忆数组memo的递归写法和使用dp数组的迭代写法。
凡事能用dp 解的题，一般也有用记忆数组的递归解法，好似一对形影不离的好基友!
DFS必然也有BFS写法！

DFS

递归思路简洁，但是OJ过不了！

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> wordSet(wordDict.begin(),wordDict.end());
        return dfs_helper(s,wordSet,0);
    }
    bool dfs_helper(string s, unordered_set<string>& wordSet, int start) {
        if (start >= s.size()) return true;
        for (int i=start+1; i<=s.size();i++) {
            if (wordSet.count(s.substr(start,i-start)) && 
            		dfs_helper(s,wordSet,i))
                return true;
        }
        return false;
    }
};

记忆数据的递归

24 ms 15.5 MB

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> wordSet(wordDict.begin(),wordDict.end());
        vector<int> memo(s.size(),-1);
        return dfs_helper(s,wordSet,0,memo);
    }
    bool dfs_helper(string s, unordered_set<string>& wordSet, 
                    int start, vector<int>& memo) {
        if (start >= s.size()) return true;
        if (memo[start] != -1) return memo[start];
        for (int i=start+1; i<=s.size();i++) {
            if (wordSet.count(s.substr(start,i-start)) && 
                    dfs_helper(s,wordSet,i,memo))
            {
                return memo[start] = 1;
            }
        }
        return memo[start] = 0;
    }
};

DP

定义dp数组跟找出状态转移方程

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> wordSet(wordDict.begin(),wordDict.end());
        vector<bool> dp(s.size()+1); dp[0]=true;
        for (int i = 0; i < dp.size(); ++i) {
            for (int j = 0; j < i; ++j) { 
                if (dp[j] && wordSet.count(s.substr(j,i-j))) {
                    dp[i] = true;
                    break;
                }
            }
        }
        return dp.back();
    }
};

W4 带访问数组BFS搜索

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> wordSet(wordDict.begin(),wordDict.end());
        vector<bool> visited(s.size()); // 和DFS的记忆数组一致
        queue<int> q{{0}};
        while (!q.empty()) {
            int start = q.front(); q.pop(); // 搜索某个起点的所有字符串
            if (!visited[start]) {
                for (int i = start + 1; i <= s.size(); ++i) {
                    if (wordSet.count(s.substr(start, i-start))) {
                        q.push(i);
                        if (i == s.size()) return true;
                    }
                }
                visited[start] = true;
            }
        }
        return false;
    }
};

L141 环形链表

给定一个链表，判断链表中是否有环。
为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置
（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

快慢指针的经典应用

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode *slow = head, *fast = head;
        while (fast && fast->next)
        {
            slow = slow->next;
            fast = fast->next->next;
            if (slow == fast) return true;
        }
        return false;
    }
};

L142 环形链表 II

---

单链表中的环 头X - 环起点Y - 快慢指针相遇点Z

1. 环的长度是多少？
   方法1 第一次相遇后，让slow,fast继续走，记录到下次相遇时循环了几次。 因为多走一圈
   方法2 第一次相遇时slow走过的距离：a+b，fast走过的距离：a+b+c+b结合速度关系得到2(a+b) = a+b+c+b，可以得到a=c，即二者第一次相遇循环的次数就等于环的长度。
2. 如何找到环中第一个节点（即Linked List Cycle II）？
   由a=c知道，第一次相遇之后，从Z和X的中点(这是有向图)即为环的第一个节点。
3. 如何将有环的链表变成单链表（解除环）？
   将第一和环节点切断即可
4. 如何判断两个单链表是否有交点？如何找到第一个相交的节点？
   判断两个链表是否有环：
   ①一个有环一个没环肯定不相交；
   ②都没有环尾部是否相等；
   ③都有环判断其中一个Z点是否在另一个链表上！

---

快慢指针

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode *cur1=head, *cur2=head;
        while (cur2 && cur2->next) {
            cur1 = cur1->next;
            cur2 = cur2->next->next;
            if (cur1 == cur2) break;
        }
        if (!cur2 || !cur2->next) return NULL;
        cur2 = head;
        while (cur1 != cur2) {
            cur1 = cur1->next;
            cur2 = cur2->next;
        }
        return cur2;
    }
};

L146 LRU(Least Recently Used)缓存机制

这道题让我们实现一个 LRU 缓存器，LRU 是 Least Recently Used 的简写，就是最近最少使用的意思。那么这个缓存器主要有两个成员函数，get 和 put:

• get 函数是通过输入 key 来获得 value，如果成功获得后，这对 (key, value) 升至缓存器中最常用的位置（顶部），如果 key 不存在，则返回 -1。
• put 函数是插入一对新的 (key, value)，如果原缓存器中有该 key，则需要先删除掉原有的，将新的插入到缓存器的顶部。如果不存在，则直接插入到顶部。
• 若加入新的值后缓存器超过了容量，则需要删掉一个最不常用的值，也就是底部的值。

class LRUCache {
private:
    int cap;
    list<pair<int,int>> l;
    unordered_map<int,list<pair<int,int>>::iterator> m;
public:
    LRUCache(int capacity) {
        cap = capacity;
    }
    int get(int key) {
        auto it = m.find(key);
        if (it == m.end()) return -1;
        // 将参数2中的参数3插入到参数1中,即插入到顶部(左)
        l.splice(l.begin(), l, it->second); 
        return it->second->second;
    }
    void put(int key, int value) {
        auto it = m.find(key);
        // 删除重复元素
        if (it != m.end()) l.erase(it->second);
        // 置顶
        l.push_front(make_pair(key,value));
        m[key] = l.begin();
        if (m.size()>cap) {
            // 底部(不活跃区域)
            int k = l.rbegin()->first;
            l.pop_back();
            m.erase(k);
        }
    }
};

L148 排序链表

在 O(nlogn) 时间复杂度和常数级空间复杂度下，对链表进行排序(升序) > 分治类排序

---

排序算法 思路整理

参考链接

• 交换类排序 – 冒泡排序 鸡尾酒排序 奇偶排序 梳子排序 侏儒排序 快速排序 臭皮匠排序 Bogo排序 :

冒泡排序(双循环+交换 n^2) ; 鸡尾酒排序(双向冒泡排序+每次进行元素前后的两次交换)
鸡尾酒算法(也是平方的算法):

// 鸡尾酒
for (int i = 0; i < a.length / 2; i++) {
  for (int j = i; 1 + j < a.length - i; j++)
    if (a[j] > a[1 + j])
      Arr.swap(a, j, 1 + j);
  for (int j = a.length - i - 1; j > i; j--)
    if (a[j - 1] > a[j])
      Arr.swap(a, j - 1, j);
}

快速排序 线性对数复杂度 最坏情况认识是平方复杂度 选基准数字 大数右放 小数左方 递归计算:

• 选择类排序 – 选择排序 堆排序 Smooth排序 笛卡尔树排序 锦标赛排序 圈排序

选择排序(尽可能最小次数的移动(保证元素不超过1的写入>圈排序) 选择最小值并移动); 圈排序();
圈排序: 3,0,2,1,4 > 0 1 2 3 4; (0,1,3)构成了一个圈
堆排序(最差、最好，乃至平均复杂度都是线性对数复杂度): 使用堆这种数据结构
平滑排序是堆排序的优化，可以将最好情况优化至线性复杂度，

• 插入类排序 – 插入排序 希尔排序 二叉查找树排序 图书馆排序 耐心排序

插入排序(将未排序元素插入最坏和平均坏的情况下都是 O(n2)，在最好的情况下是 O(n))
希尔排序(缩小增量排序): 不如线性对数但是对基本有序小数组排序时十分高效，代码就是在冒泡排序的外层循环加上gap的循环：

const int n = 5;
int i, j, temp;
int gap = 0;
int a[] = {5, 4, 3, 2, 1};
while (gap<=n)
{
  gap = gap * 3 + 1;
}
while (gap > 0)
{
  for ( i = gap; i < n; i++ )
  {
    j = i - gap;
    temp = a[i];
    while (( j >= 0 ) && ( a[j] > temp ))
    {
      a[j + gap] = a[j];
      j = j - gap;
    }
    a[j + gap] = temp;
  }
  gap = ( gap - 1 ) / 3;
}

• 归并类排序 – 归并排序 梯级归并排序 振荡归并排序 多相归并排序 Strand排序

归并排序: 平均时间复杂度 O(nlogn)，最好时间复杂度 O(n)
1申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
2设定两个指针，最初位置分别为两个已经排序序列的起始位置；
3比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
4重复步骤直到某一指针达到序列尾；
5将另一序列剩下的所有元素直接复制到合并序列尾。

• 分布类排序 – 美国旗帜排序 珠排序 桶排序 计数排序 基数排序 鸽巢排序 相邻图排序

桶排序:

function bucket-sort(array, n) is
  buckets ← new array of n empty lists
  for i = 0 to (length(array)-1) do
    insert array[i] into buckets[msbits(array[i], k)]
  for i = 0 to n - 1 do
    next-sort(buckets[i])
  return the concatenation of buckets[0], ..., buckets[n-1]

计数排序: 计数排序使用一个额外的数组 C，其中第 i 个元素是待排序数组 A 中值等于 i 的元素的个数。当输入的元素是 n 个 0 到 k 之间的整数时，它的运行时间是 O(n + k)。计数排序不是比较排序，排序的速度快于任何比较排序算法。

private static void countingSort(int[] A, int[] B, int k) {
    int[] C = new int[k];
    // 计数
    for (int j = 0; j < A.length; j++) {
        int a = A[j];
        C[a] += 1;
    }
    // 求计数和
    for (int i = 1; i < k; i++) {
        C[i] = C[i] + C[i - 1];
    }
    // 整理
    for (int j = A.length - 1; j >= 0; j--) {
        int a = A[j];
        B[C[a] - 1] = a;
        C[a] -= 1;
    }
}

• 混合类排序 – Tim排序 内省排序 Spread排序 UnShuffle排序 J排序

---

TODO
… …

L152 乘积最大子数组

动态规划

$$\begin{gathered} f_{\max }(i)=\underset{i=1}{\overset{n}{\max }}\left\{f_{\max }(i-1)\times a_i,f_{\min }(i-1)\times a_i,a_i\right\} \\ {f}_{\min }(i)=\underset{i=1}{\min }\left\{f_{\max }(i-1)\times a_i,f_{\min }(i-1)\times a_i,a_i\right\} \end{gathered}$$

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        vector <int> maxF(nums), minF(nums);
        for (int i = 1; i < nums.size(); ++i) {
            maxF[i] = max(maxF[i - 1] * nums[i], max(nums[i], minF[i - 1] * nums[i]));
            minF[i] = min(minF[i - 1] * nums[i], min(nums[i], maxF[i - 1] * nums[i]));
        }
        return *max_element(maxF.begin(), maxF.end());
    }
};

左右遍历

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int res = nums[0], prod = 1, n = nums.size();
        for (int i = 0; i < n; ++i) {
            res = max(res, prod *= nums[i]);
            if (nums[i] == 0) prod = 1;
        }
        prod = 1;
        for (int i = n - 1; i >= 0; --i) {
            res = max(res, prod *= nums[i]);
            if (nums[i] == 0) prod = 1;
        }
        return res;
    }
};

L155 最小栈

设计一个支持 push，pop，top 操作，并能在常数时间内检索到最小元素的栈。
push(x) -- 将元素 x 推入栈中。
pop() -- 删除栈顶的元素。
top() -- 获取栈顶元素。
###
getMin() -- 检索栈中的最小元素。

双栈法

class MinStack {
private: stack<int> s1, s2;
public:
    /** initialize your data structure here. */
    MinStack() {}
    void push(int x) {
        s1.push(x);
        if (s2.empty() || x <= s2.top()) 
        { // x< 会报错 因为可能push的是NULL
          // pop时s1和s2要同时pop的，所以NULL也得push进
            s2.push(x);
        }
    }
    void pop() {
        if (s1.top() == s2.top()) s2.pop();
        s1.pop();
    }
    int top() {
        return s1.top();
    }
    int getMin() {
        return s2.top();
    }
};

最小值记录法

class MinStack {
private: 
    stack<int> s; 
    int min_val;
public:
    /** initialize your data structure here. */
    MinStack() {min_val = INT_MAX;}
    void push(int x) {
        if (x <= min_val) 
        { // 前一个最小值push进当前最小值下面
            s.push(min_val);
            min_val = x;
        }
        s.push(x);
    }
    void pop() {
        int t = s.top(); s.pop();
        if (t == min_val) 
        { // pop栈的时候 也要载入次最小值
            min_val = s.top(); s.pop();
        }
    }
    int top() {
        return s.top();
    }
    int getMin() {
        return min_val;
    }
};

L160 相交链表

算长度+同时查找

不足之处：ERROR: linked structure was modified.！！！

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        if (!headA || !headB) return NULL;
        int lenA = getLength(headA);
        int lenB = getLength(headB);
        if (lenA < lenB) {
            for (int i = 0; i < lenB - lenA; i++) {
                headB = headB->next;
            }
        } else {
            for (int i = 0; i < lenA - lenB; i++) {
                headA = headA->next;
            }
        }
        while (headA && headB && headA != headB) {
            headA = headA->next;
            headB = headB->next;
        }
        return (headA && headB) ? headA : NULL;
    }
    int getLength(ListNode *head) {
        int cnt = 0;
        while (head) {
            ++cnt;
            head = head->next;
        }
        return cnt;
    }
};

快慢指针

哈希表

看作8字环形链表

其中一条遍历到末尾时，我们跳到另一个条链表的开头继续遍历
在交点处或在各自尾节点相遇

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, 
                                  ListNode *headB) 
{
        if (!headA || !headB) return NULL;
        ListNode *a = headA, *b = headB;
        while (a != b)
        {
            a = a ? a->next : headB;
            b = b ? b->next : headA;
        }
        return a;
    }
};

L169 多数元素

中文翻译是，求一个数组中的众数
但是应该是翻译错了！(Mode是数学中的众数翻译！)
题目中要求是 appears more than ⌊ n/2 ⌋ times
这个元素得是超过一半数组长的元素！
此题中 输入数组 一定有过半数的存在

Moore Voting

注意 数组中存在频数大于1/2长度的元素，当减到0 则当前不是候选和候选的数目相同了，减到0之后需要更换候选者！就算后面又出现了，到时候由于前面的强大前提，必然重新切换为候选者！

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int res = 0, cnt = 0;
        for (int num : nums)
        {
            if (cnt == 0) {res = num; ++cnt;}
            else (num == res) ? ++cnt : --cnt;
        }
        return res;
    }
};

Bit Manipulation

int是32位，对数组中每个数组元素统计各个位的0和1出现频率，多的那个选为该位的元素(1 0)

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int res = 0, n = nums.size();
        for (int i = 0; i < 32; i++)
        {
            int onesNum = 0, zerosNum = 0;
            for (int num : nums)
            {
                if (onesNum > n / 2 || zerosNum > n / 2) break;
                if ((num & (1 << i)) != 0) ++onesNum;
                else ++zerosNum;
            }
            if (onesNum > zerosNum) res |= (1 << i);
        }
        return res;
    }
};

排序取中位数

L198 打家劫舍

经典的动态规划问题

DP

class Solution {
public:
    int rob(vector<int>& nums) {
        if (nums.size() == 0) 
            return 0;
        if (nums.size() == 1) 
            return nums[0];
        if (nums.size() == 2) 
            return max(nums[0], nums[1]);
        if (nums.size() == 3) 
            return max(nums[0] + nums[2], nums[1]);
        vector<int> inte = {nums[0], nums[1], 
                            nums[0] + nums[2]};
        int M = max(inte[0], max(inte[1], inte[2]));
        for (int i = 3; i < nums.size(); i++)
        {
            int tmp = max(inte[i - 2] + nums[i], 
                          inte[i - 3] + nums[i]);
            M = max(tmp, M);
            inte.push_back(tmp);
        }
        return M;
    }
};

DP2

class Solution {
public:
    int rob(vector<int>& nums) {
        if (nums.size() <= 1) 
            return nums.empty() ? 0 : nums[0];
        vector<int> dp = {nums[0], 
                          max(nums[0], nums[1])};
        for (int i = 2; i < nums.size(); i++)
        {
            dp.push_back(max(nums[i] + dp[i - 2], 
                         dp[i - 1]));
        }
        return dp.back();
    }
};

DP3

class Solution {
public:
    int rob(vector<int>& nums) {
        int robEven = 0, robOdd = 0, n = nums.size();
        for (int i = 0; i < n; ++i) {
            if (i % 2 == 0) {
                robEven = max(robEven + nums[i], robOdd);
            } else {
                robOdd = max(robEven, robOdd + nums[i]);
            }
        }
        return max(robEven, robOdd);
    }
}; 

DP4

class Solution {
public:
    int rob(vector<int>& nums) {
        int robEven = 0, robOdd = 0, n = nums.size();
        for (int i = 0; i < n; ++i) {
            if (i % 2 == 0) {
                robEven = max(robEven + nums[i], robOdd);
            } else {
                robOdd = max(robEven, robOdd + nums[i]);
            }
        }
        return max(robEven, robOdd);
    }
};

200 岛屿数量

4连通域问题

DFS

class Solution {
public:
    int numIslands(vector<vector<char>>& grid) {
        if (grid.empty() || grid[0].empty()) return 0;
        int h = grid.size(), w = grid[0].size();
        vector<vector<bool>> visited(h, vector<bool>(w, false));
        int rev = 0;
        for (int i = 0; i < h; ++i) {
            for (int j = 0; j < w; ++j) {
                if (grid[i][j] == '0' || visited[i][j]) continue;  // TNT!
                helper(grid, visited, i, j);
                ++rev;
            }
        }
        return rev;
    }
    void helper(vector<vector<char>>& grid, vector<vector<bool>>& visited, int i, int j) {
        if (i < 0 || i >= grid.size()) return;
        if (j < 0 || j >= grid[0].size()) return;
        if (grid[i][j] == '0' || visited[i][j]) return;
        visited[i][j] = true;
        helper(grid, visited, i-1, j);
        helper(grid, visited, i, j-1);
        helper(grid, visited, i+1, j);
        helper(grid, visited, i, j+1);
    }
};

BFS

class Solution {
public:
    int numIslands(vector<vector<char>>& grid) {
        if (grid.empty() || grid[0].empty()) return 0;
        int h = grid.size(), w = grid[0].size();
        vector<vector<bool>> visited(h, vector<bool>(w, false));
        int rev = 0;
        for (int i = 0; i < h; ++i) {
            for (int j = 0; j < w; ++j) {
                if (grid[i][j] == '0' || visited[i][j]) continue;
                rev++;
                // BFS
                std::queue<std::pair<int,int>> q{{std::pair<int,int>(i,j)}};
                std::vector<std::pair<int,int>> delta;
                delta.push_back(make_pair<int,int>(-1,0));
                delta.push_back(make_pair<int,int>(1,0));
                delta.push_back(make_pair<int,int>(0,-1));
                delta.push_back(make_pair<int,int>(0,1));
                while(!q.empty()) {
                    auto ht = q.front(); q.pop();
                    for (auto& d : delta) {
                        auto htd = ht; htd.first += d.first; htd.second += d.second;
                        int y = htd.first, x = htd.second;
                        if (y < 0 || y >= h || x < 0 || x >= w || grid[y][x] == '0' || visited[y][x]) 
                            continue;
                        visited[y][x] = true;
                        q.push(htd);
                    }
                }
            }
        }
        return rev;
    }
};

L206 反转链表

迭代

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* head2 = head;
        ListNode* tail = NULL;
        while(head2) {
            auto tmp = head2->next; // 断
            head2->next = tail; // 接
            tail = head2; // 换
            head2 = tmp;
        }
        return tail;
    }
};

递归

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if (!head || !head->next) return head;
        ListNode* head2 = reverseList(head->next);
        head->next->next = head;
        head->next = NULL; // 回溯有现场记录下head一路的值
        return newhead; // newhead不要修改
    }
};

L207 课程表

有向图的环检测

BFS 拓扑排序

拓扑排序主要用于任务调度，按先后顺序进行排序，应用包括计算机指令调度，指令为顶点，有方向表示按顺序执行。
计算各个顶点的入度，构建邻接链表；
寻找入度为0的起点，开始搜索；
每次搜索到顶点则将其入度减一，即断开；
搜索完成仍然存在入度非0点，则一定存在环。

class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> graph(numCourses, vector<int>());
        vector<int> in(numCourses);
        queue<int> q;
        for (auto& pre : prerequisites) {
            graph[pre[1]].push_back(pre[0]);  // pre[1]->pre[0]
            in[pre[0]]++;
        }
        for (int i = 0; i < numCourses; ++i) {
            if (in[i] == 0) q.push(i);
        }
        while (!q.empty()) {
            int ft = q.front(); q.pop();  // 出队顺序就是拓扑顺序
            for (auto& gra : graph[ft]) {
                in[gra]--;
                if (in[gra] == 0) q.push(gra);
            }
        }
        for (int i = 0; i < numCourses; ++i) {
            if (in[i] != 0) return false;
        }
        return true;
    }
};

DFS

class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> graph(numCourses, vector<int>());
        vector<int> visited(numCourses, 0);
        for (auto& pre : prerequisites) {
            graph[pre[1]].push_back(pre[0]);
        }
        for (int i = 0; i < numCourses; ++i) {
            if (!canDFS(graph, visited, i)) return false;
        }
        return true;
    }
    bool canDFS(vector<vector<int>>& graph, vector<int>& visited, int i) {
        if (visited[i] == -1) return false;
        if (visited[i] == 1) return true;
        visited[i] = -1; // 访问
        for (auto& g : graph[i]) {
            if (!canDFS(graph, visited, g)) return false;
        }
        visited[i] = 1; // i访问到头了
        return true;
    }
};

L208 实现Trie (前缀树)

字典树：
1 根节点不含字符, 其余节点只含一个字符
2 根节点到其余节点连起来就是字符串
3 每个节点的的所有子节点的字符都不同

三种儿子节点指向方法：
1 数组形式的子节点
2 链表形式的子节点
3 左儿子右父亲表示字母树

class TrieNode {
public:
    TrieNode *child[26];
    bool isWord;
    TrieNode() : isWord(false) {
        for (auto& a : child) a = nullptr;
    }
};

class Trie {
public:
    /** Initialize your data structure here. */
    Trie() {
        root = new TrieNode();
    }
    
    /** Inserts a word into the trie. */
    void insert(string word) {
        TrieNode *p = root;
        for (auto& a : word) {
            int index = a - 'a';
            if (!p->child[index]) p->child[index] = new TrieNode();
            p = p->child[index];
        }
        p->isWord = true;
    }
    
    /** Returns if the word is in the trie. */
    bool search(string word) {
        TrieNode *p = root;
        for (auto& a : word) {
            int index = a - 'a';
            if (!p->child[index]) return false;
            p = p->child[index];
        }
        return p->isWord;
    }
    
    /** Returns if there is any word in the trie that starts with the given prefix. */
    bool startsWith(string prefix) {
        TrieNode *p = root;
        for (auto& a : prefix) {
            int index = a - 'a';
            if (!p->child[index]) return false;
            p = p->child[index];
        }
        return true;
    }

private:
    TrieNode* root;
};

L215 数组中的第K个最大元素

寻找K次

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        int len = nums.size();
        if (k > len) return -1;
        vector<bool> labels(len, true);
        int rev;
        while (k--) {
            int L = INT_MIN, la = -1;
            for (int i = 0; i < len; ++i) {
                if (labels[i] && nums[i] > L) {
                    la = i;
                    L = nums[i];
                }
            }
            labels[la] = false;
            rev = L;
        }
        return rev;
    }
};

排序后查询$>$接题148的排序算法介绍

STL自带排序算法（快排）

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        sort(nums.rbegin(), nums.rend());
        return nums[k-1];
    }
};

STL自带排序的数据结构（二叉搜索树或堆）

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        priority_queue<int> q{less<int>(),nums};
        k--;
        while (k--) q.pop();
        return q.top();
    }
};

交换类排序 冒泡+快排

冒泡排序

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        bubbleSort(nums);
        return nums[nums.size()-k];
    }
    void bubbleSort(vector<int>& data) {
        int n = data.size();
        bool again = true;
        for(int i = 0;  i < n-1 && again; i++) {
            for(int j = n-1, again = false; j > i; j--) {
                if(data[j] < data[j-1]) {
                    swap(data[j], data[j-1]);
                    again = true;
                }
            }
        }
    }
};

快速排序

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        quickSort(nums, 0, nums.size() - 1);
        return nums[nums.size()-k];
    }
    void quickSort(vector<int>& nums, int left, int right) {
        if (left >= right) return;
        int pivot = nums[left];
        int mid = (left + right) / 2;
        int c1 = left, c2 = right;
        while (c1 < c2) {
            while (nums[c2] > pivot && c1 < c2) c2--;
            if (c1 < c2) nums[c1++] = nums[c2];
            while (nums[c1] <= pivot && c1 < c2) c1++;
            if (c1 < c2) nums[c2--] = nums[c1];
        }
        nums[c1] = pivot;
        quickSort(nums, left, c1-1);
        quickSort(nums, c1+1, right);
    }
};

注意快速排序这里，不需要将序列全部排完序，利用快速排序的思想：

• 当有k-1个数在pivot之前，则该pivot就是第k大的数，如下：

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        int left = 0, right = nums.size() - 1;
        while (true) {
            int pos = partition(nums, left, right);
            if (pos == k - 1) return nums[pos];
            else if (pos > k - 1) right = pos - 1;
            else left = pos + 1;
        }
    }
    int partition(vector<int>& nums, int left, int right) {
        int pivot = nums[left], c1 = left + 1, c2 = right;
        while (c1 <= c2) {
            if (nums[c1] < pivot && nums[c2] > pivot) {
                swap(nums[c1++], nums[c2--]);
            }
            if (pivot <= nums[c1]) c1++;
            if (pivot >= nums[c2]) c2--; 
        }
        swap(nums[left], nums[c2]);
        return c2;
    }
};

选择类排序 选排+堆排

选择排序

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        selectionSort(nums);
        return nums[nums.size()-k];
    }
    void selectionSort(vector<int>& data) {
        int n = data.size();
        for(int i = 0, j,min; i < n-1; i++) {
            for(j = i+1, min = i; j < n; j++)
                if(data[j] < data[min]) min = j;
            swap(data[i], data[min]);
        }
    }
};

堆排序

就是STL中priority_queue数据类型，默认使用vector类型构建
堆:
1 完全二叉树：子节点不超过2个，且先序遍历到一个NULL即到结尾
2 父节点要么比子节点小要么大 小顶堆或大顶堆
3 关键性质：

• 3.1 按层次遍历输出数组序号，k节点的父节点(k-1)/2，左子节点2k+1，右节点2k+2
• 3.2 获得大顶堆的步骤:
• • (1) 从第二层(叶节点处第一层)开始，提取最小值往上(即类似最小堆的思路)移到根节点
• • (2) 将根节点和最末(最右叶节点)交换元素，最末节点就是有序了。之后循环，不断以根节点为起始在无序区提取最小值到根节点，再和无序区的尾元素交换。

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        heapSort(nums);
        return nums[k-1];
    }
    void heapBuild(vector<int>& nums, int root, int end) {
	// 就是小顶堆的下沉操作，将root处元素在0~end间下沉到不能下为止
        int left = 2 * root + 1;
        if (left >= end) return;
        int right = left + 1;
        // 左右子节点中的较小值序号
        int minInx = ((right<end)&&(nums[right]<nums[left])) ? right : left; 
        if (nums[minInx] < nums[root]) {
            swap(nums[minInx], nums[root]);
            heapBuild(nums, minInx, end);
        }
    }
    void heapSort(vector<int>& nums) {
        // 初始化完全二叉树->先小顶堆方式 提取最小值到0处
        for (int i = nums.size() / 2 - 1; i >= 0; --i) {
        // 从倒数第二层开始开始将大值下沉，或者说小值上升
            heapBuild(nums, i, nums.size());
        }
        for (int i = nums.size() - 1; i > 0; --i) {
            // 交换头尾 将最小值往未排序的后面节点放
            swap(nums[0], nums[i]);
            heapBuild(nums, 0, i);
        }
    }
};

插入类排序 插排+希尔

插入排序

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        insertSort(nums);
        return nums[nums.size()-k];
    }
    void insertSort(vector<int>& nums) { // 插入排序
        if (nums.size() < 2) return;
        for (int i = 1; i < nums.size(); ++i) {
            for (int j = i - 1; j >= 0 && nums[j] > nums[j + 1]; --j) 
                swap(nums[j], nums[j + 1]);
        }
    }
};

希尔排序

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        shellSort(nums);
        return nums[nums.size()-k];
    }
    void shellSort(vector<int>& nums)