第四章 搜索

第四章 搜索

完整代码下载

第一节 全排列

123的全排列为123 132 213 231 312 321

我们也可以用一个三重循环嵌套

for(a=1;a<=3;a++)
	for(b=1;b<=3;b++)
		for(c=1;c<=3;c++)
			if(a!=b&& a!=c&&b!=c)
				printf("%d%d%d\n",a,b,c)

但是如果个数很多的话，写起来就很麻烦

第二节 深度优先搜索

我们可以将上一节的问题简化为三张牌放入3个盒子里

for(i=1;i<=n;i++)
{
	if(book[i]==0)	//book[i]==0表示第i号牌还在手上
	{
		a[step]=i;	//将i号牌放入第step个盒子中
		book[i]=1;	//将book[i]设为1，表示i号牌不在手上
	}
}

我们将刚刚的代码封装为一个函数就可以去处理余下的牌了

viod dfs(ints step)//step表示在第几个盒子前
{
    for(i=1;i<=n;i++)
    {
        if(book[i]==0)	//book[i]==0表示第i号牌还在手上
        {
            a[step]=i;	//将i号牌放入第step个盒子中
            book[i]=1;	//将book[i]设为1，表示i号牌不在手上
            dfs(step+1);//函数递归调用
            book[i]=0;//收回刚刚的牌
        }
    }	
}

深度优先搜索的基本模型

void dfs(int step)
{
	判断边界
	尝试每一种可能 for(i=1;i<=n;i++)
	{
		继续下一步	dfs(step+1);
	}
	返回
}

那么完整的代码

//算法10
int a[10],book[10],n;
void dfs(int step)//step表示在第几个盒子前
{
    int i;
    if(step==n+1)
    {
        for(i=1;i<=n;i++)
            printf("%d",a[i]);
        printf("\n");
        
        return;
    }
    
    for(i=1;i<=n;i++)
    {
        if(book[i]==0)
        {
            a[step]=i;
            book[i]=1;
            
            dfs(step+1);
            book[i]=0;
        }
    }
    return;
}

第三节 广度优先搜索

广度优先搜索又称宽度优先搜索

我用它来解决一个迷宫问题：

//算法11
{
    struct note que[2501];
    
    int a[51][51]={0},book[51][51]={0};
    
    int next[4][2]={{0,1},
                    {1,0},
                    {0,-1},
                    {-1,0}};
    int head,tail;
    int i,j,k,n,m,startx,starty,p,q,tx,ty,flag;
    
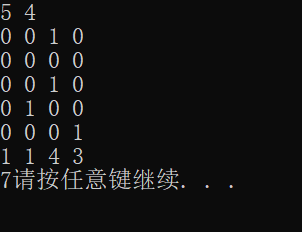
    scanf("%d %d",&n,&m);
    for(i=1;i<=n;i++)
        for(j=1;j<=m;j++)
            scanf("%d",&a[i][j]);
        scanf("%d %d %d %d",&startx,&starty,&p,&q);
    //对列初始化
    head=1;
    tail=1;
    //插入迷宫入口的坐标
    que[tail].x=startx;
    que[tail].y=starty;
    que[tail].f=0;
    que[tail].s=0;
    tail++;
    book[startx][starty]=1;
    
    flag=0;//用来标记是否到达目标点
    while(headn||ty<1||ty>m)
                continue;
            //判断是否为障碍物
            if(a[tx][ty]==0&&book[tx][ty]==0)
            {
                book[tx][ty]=1;
                
                que[tail].x=tx;
                que[tail].y=ty;
                que[tail].f=head;
                que[tail].s=que[head].s+1;
                tail++;
            }
            if(tx==p&&ty==q)
            {
                flag=1;
                break;
            }
        }
        if(flag==1)
            break;
        head++;
    }
    
    printf("%d",que[tail-1].s);
    
    system("pause");
    return 0;
}