高斯定理与电场的散度

在这之前，我们先了解一下通量的概念。考虑一根自来水管，水管内的水向右流动，如下图所示。

在水管中取一个截面$dS$，那么在单位时间内，通过这个截面的水是一定的，即通过这个截面的水的量。那么这个量又是什么呢？

通量通常是针对矢量而言的。在这里，取水流速度的大小$v$与截面的面积$dS$的乘积$vdS$，得到速度通量，再乘上通过该截面的水的质量$m$，得到动量通量$mvdS$。

上面这种情况是水流与截面垂直的情况，当水流与截面不垂直的时候，如下图所示，还能这样计算通量吗？

我们先给这个截面增加一个方向，这个方向为截面的法向（即与截面垂直），并且只能与水流的方向平行或者成一个锐角。随后将黄色箭头所代表的矢量，例如动量$p$，分解，一部分平行于$dS$，另一部分垂直于$dS$。像这样只有平行于$dS$的矢量才能通过这个面，设这个矢量与$dS$的夹角为$\theta$，则通量为
$$p\cos \theta dS=p\cdot dS\text{\hspace{1em}(1)}$$
即一个矢量在某个面元上的通量，只需将这个矢量与面元所构成的矢量做内积即可。

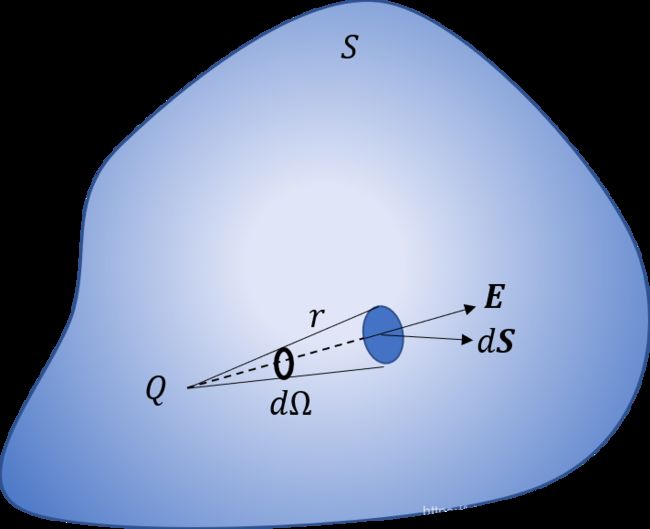
现在考虑电场$E$的通量。假设有一个静电荷$Q$，它被一个闭合曲面$S$包围，如下图所示。

在曲面上取一个有向面元$dS$，以法线向外为正方向。则电荷$Q$在面元$dS$处产生的电场的通量为
$$E\cdot dS=E\cos \theta dS=\frac{Q}{4\pi {\epsilon }_0{r}^2}\cos \theta dS\text{\hspace{1em}(2)}$$

其中$\theta$为$r$与$dS$的夹角（即$dS$与电荷$Q$在该面元处的夹角）。

现在我们来看$\cos \theta dS$的含义。以$Q$为球心，$r$为半径，作一个球面。那么$\theta$就是面元$dS$与该处球面法向的夹角，所以$\cos \theta dS$就是面元$dS$投影到球面上的面积。那么$\cos \theta dS/r^2$就是面元$dS$对电荷$Q$所张开的立体角元$d\Omega$。

那么什么是立体角呢？先回忆一下弧度的定义。在一个扇形中，这个扇形的弧长除以扇形的半径，就是这个扇形的圆心角所对应的弧度。立体角与弧度类似，只不过弧度是由圆来定义，而立体角是由球来定义。取一个球面，用这个球面的面积除以这个球的半径的平方，得到的就是这个球面对应的立体角。立体角与弧度一样，它与球的具体半径无关，只表示三维空间中角度的大小。在平面几何中，根据弧度的定义，一个圆周的弧度，可以用圆的周长比上圆的半径，其结果为$2\pi$。同理，一个球所对应的立体角，可以用球的面积除以球的半径的平方，其结果为$4\pi$。即封闭曲面对封闭曲面内任意一点，所张的立体角都是$4\pi$

$$\oint d\Omega =4\pi$$

由于式(2)计算的是面元处的电场通量，要计算整个闭合曲面的通量，还需要对整个闭合曲面$S$进行积分：
$${\oint }_{S}E\cdot dS=\frac{Q}{4\pi {\epsilon }_0}\oint d\Omega =\frac{Q}{{\epsilon }_0}\text{\hspace{1em}(3)}$$

式(3)即为电场通量的高斯定理
$${\oint }_{S}E\cdot dS=\frac{Q}{{\epsilon }_0}\text{\hspace{1em}(4)}$$

即闭合曲面的电场通量只与闭合曲面内的电荷有关，与闭合曲面外的电荷无关。这是因为闭合曲面外的电荷产生的电场，从闭合曲面的一个位置进入，必定会从闭合曲面的另外一个位置出来，对闭合曲面的电场通量没有贡献。

在方程(4)左右两边同时除以该闭合曲面所围的体积$\Delta V$，随后让这个体积无限缩小，即$\Delta V\to 0$，最后可以得到电通量强度与电荷密度之间的关系
$$\nabla \cdot E=\frac{\rho }{{\epsilon }_0}\text{\hspace{1em}(5)}$$

高斯定理揭示了电荷密度分布与产生的电场之间的关系。由于数学上的相似性，高斯定理也可以应用于其它由平方反比律决定的物理量，例如引力或者辐照度。

---

欢迎关注微信公众号“理工学派”（ID: sciengpi），获取更多自然科学方面的文章。