Dijkstra(狄克斯特拉)求加权重的邻接矩阵最短路径（初级版）

算法

参考资源：https://www.geeksforgeeks.org/dijkstras-shortest-path-algorithm-greedy-algo-7/

百度百科：迪杰斯特拉算法是于1959 年由荷兰计算机科学家狄克斯特拉提出的。是从一个节点到其余各节点的最短路径算法，解决的是有向或者无向加权重图中最短路径问题。迪杰斯特拉算法的主要特点是以起始点为中心，向外层层扩展，应用了典型的贪心算法。
1）创建一个集sptSet（最短路径集），它跟踪最短路径中包含的顶点，即，计算并最终确定与源的最小距离。 最初，这个集合是空的。
2）为输入图中的所有顶点指定距离值。 将所有距离值初始化为INFINITE。 将源顶点的距离值指定为0，以便首先拾取它。
3）虽然sptSet不包括所有顶点
     a）选择sptSet中不存在的顶点u并且具有最小距离值。
     b）将你包括在sptSet中。
     c）更新u的所有相邻顶点的距离值。 要更新距离值，请遍历所有相邻顶点。 对于每个相邻顶点v，如果u（来自源）和边缘u-v的权重的距离值之和小于v的距离值，则更新v的距离值。

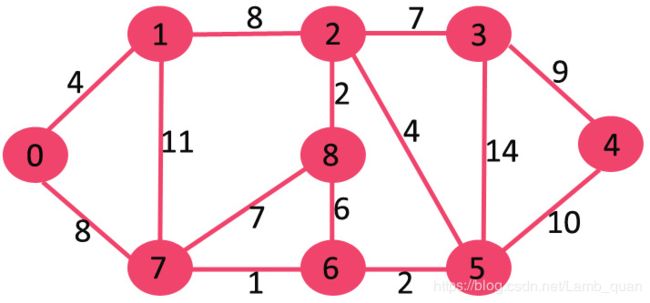
如图所示：无向图

Java构建邻接矩阵：

              new int[][]{{0, 4, 0, 0, 0, 0, 0, 8, 0},
                                {4, 0, 8, 0, 0, 0, 0, 11, 0},
                                {0, 8, 0, 7, 0, 4, 0, 0, 2},
                                {0, 0, 7, 0, 9, 14, 0, 0, 0},
                                {0, 0, 0, 9, 0, 10, 0, 0, 0},
                                {0, 0, 4, 14, 10, 0, 2, 0, 0},
                                {0, 0, 0, 0, 0, 2, 0, 1, 6},
                                {8, 11, 0, 0, 0, 0, 1, 0, 7},
                                {0, 0, 2, 0, 0, 0, 6, 7, 0}
                                }

Java程序：

package shu_quan.greedy;


import java.util.*; 

import java.lang.*; 
import java.io.*; 

/**
 * 
 * @author //代码由 Aakash Hasija and Lamb_quan提供
 *
 */
/*
 *  针对带权重（非负）邻接矩阵图的算法，使用Java语言实现狄克斯特拉（Dijkstra）算法，
 *  解决单源最短路径问题。
 */
 
class ShortestPathWithList 
{ 
 
	//找出当前节点u到节点v（还没有包括在最短路径中的节点）的最小值
	static final int V=9; 
	int minDistance(int dist[], Boolean sptSet[]) 
	{ 
		// 初始化最小值为无穷大的替代形式
		int min = Integer.MAX_VALUE, min_index=-1; 

		for (int v = 0; v < V; v++) 
			if (sptSet[v] == false && dist[v] <= min) 
			{ 
				min = dist[v]; 
				min_index = v; 
			} 

		return min_index; 
	} 

	// 该函数是输出函数，打印结果
	void printSolution(int dist[], int n,ArrayList> allPath) 
	{ 
	   System.out.println("运行结果如下："); 
	   for (int i = 0; i < V; i++) 
	   System.out.println("源节点到节点"+i+"最短路径长度为："+dist[i]+"     径路为："+allPath.get(i)); 
	} 


	//该函数实现了邻接矩阵表示图的Dijkstra单源最短路径算法
	void dijkstra(int graph[][], int src) 
	{ 
		//输出数组为源节点src到目的节点i的最短路径值dist[i]
		int dist[] = new int[V]; 

		//，如果节点i被包含在从源节点到i节点的最短路径中，那么就将对应的节点设置true
		Boolean sptSet[] = new Boolean[V]; 

		//初始化全部标志为默认false，最短路径距离值为无穷大的替代形式。
		for (int i = 0; i < V; i++) 
		{ 
			dist[i] = Integer.MAX_VALUE; 
			sptSet[i] = false; 
		} 
		
		//初始化容器V条路径，默认应该是null
		ArrayList> allPath = new ArrayList>();
		for (int i = 0; i < V; i++) {
			allPath.add(new ArrayList<>());
		}

		// 源节点到自己的距离为 0 
		dist[src] = 0; 


		// 找出所有节点的最短路径
		for (int count = 0; count < V; count++) 
		{ 

			//从未被标记的所有最短路径值的集合中，找出值最小的节点作为u节点。
			//第一次总是源节点本身。
			int u = minDistance(dist, sptSet); 
			
			//选择起点		
			ArrayList onePath = allPath.get(u);
			onePath.add(u);

			// 被选的u节点作为最短路径的过渡节点并且标记true 
			sptSet[u] = true; 

			// Update dist value of the adjacent vertices of the 
			// picked vertex. 
			//更新可达的相邻的节点的最短路径值
			for (int v = 0; v < V; v++) 
				
				//1、只会更新还未被标记的节点，且满足到邻近节点的距离不能为0，
				//2、满足过渡节点的最短路径值不能无穷大，
				//3、满足加上邻近节点的最短路径值小于之前到该临近节点的值
				//条件全部满足更新最短路径值，并添加该节点更新路径
			if(!sptSet[v] && graph[u][v]!=0 && dist[u] != Integer.MAX_VALUE 
			   && dist[u]+graph[u][v] < dist[v]) {
								
					dist[v] = dist[u] + graph[u][v]; 
					/* 
					 * 增加节点比之前的路径短，因此要复制之前的路径再加上此节点
					 */
					//获取该节点对应的路径
					ArrayList localPath = allPath.get(v);
					//复制之前先清空路径。
					localPath.clear();
					//将上一个状态包括u节点的路径联结到此节点v
					localPath.addAll(onePath);	
					//不包含此节点就添加该节点
					if(localPath.contains(v)) {							
						localPath.add(v);
					}
					
				}
		} 

		// 输出结果：源节点到每个节点的距离，具体路径 
		printSolution(dist, V, allPath); 
		//打印标记
		for (int i = 0; i < V; i++) 
			System.out.println(i+" 标记： "+sptSet[i]); 
	} 

	// main函数
	public static void main (String[] args) 
	{ 
		/* 创建一个带权重的无向邻接矩阵的图 */
	int graph[][] = new int[][]{
		{0, 4, 0, 0, 0, 0, 0, 8, 0}, 
		{4, 0, 8, 0, 0, 0, 0, 11, 0}, 
		{0, 8, 0, 7, 0, 4, 0, 0, 2}, 
	        {0, 0, 7, 0, 9, 14, 0, 0, 0}, 
		{0, 0, 0, 9, 0, 10, 0, 0, 0}, 
		{0, 0, 4, 14, 10, 0, 2, 0, 0}, 
		{0, 0, 0, 0, 0, 2, 0, 1, 6}, 
		{8, 11, 0, 0, 0, 0, 1, 0, 7}, 
		{0, 0, 2, 0, 0, 0, 6, 7, 0} 
								}; 
		ShortestPathWithList t = new ShortestPathWithList(); 
		t.dijkstra(graph, 0); 
	} 
} 

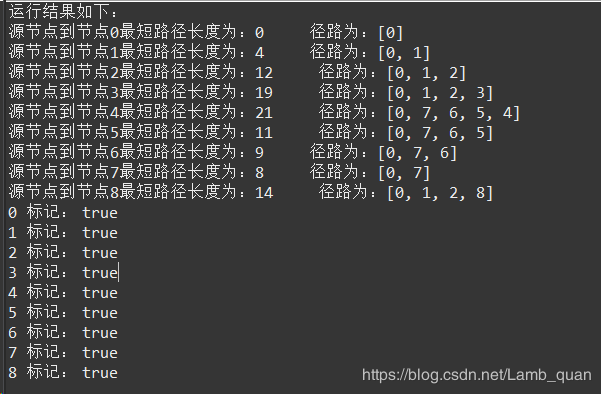
控制台输出：