PyTorch入门实战教程笔记（二）：简单回归问题。

PyTorch入门实战教程笔记（二）：简单回归问题

引入

在学之前先讲解一下梯度下降算法，因为梯度就是深度学习的核心精髓。举个例子，一个简单的函数，我们定义函数 loss = x^2*sin(x),求这个函数的极值，即求导，使倒数等于零。梯度下降算法与其极其类似，不同的是有一个迭代的过程。如下图y’为该函数的导数。梯度下降算法就是，每次得到一个导数，使用x的值减去导数的值▽x，得到新的x’的值，即x’ = x - ▽x,就完成了一次迭代，每一步迭代就是一个梯度下降。然后新的x’，再按照上面的步骤，朝着梯度下降的方向，循环迭代。

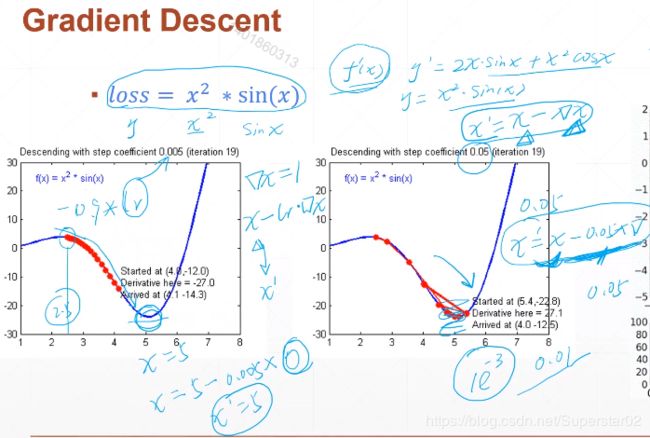
　　如上图，比如x=2.5，导数 ▽x大概为-0.9，则x’= 2.5 - lr×（-0.9）。lr是什么呢，是learning rate，即学习率，乘以一个学习率，能够使x’的变化量比较小，达到左边图的效果。若学习率不合适（比如过大），会出现距离的波动（右图），这是不理想的。这也是我们为什么需要learning rate的原因。左图例如x=5，梯度（导数）为0，那么计算后，x’依然等于5，就达到了我们的目的。

求解一个简单的二元一次方程

举例如下图：

　　大家应该听过训练参数Ｗ和ｂ，而在这个简单的二元一次方程根据两个（x，y）点即可求得W,b。但是在现实中的数据会有一定的误差或者噪声。故在求解时，向数据加入随机造成更符合实际情况，比如在数据后面添加一个均值为0.01，方差为1的高斯噪声。这样如果只观察两组数据，得到的误差比较大，所以应观测一组数据，来求解整组参数最合适的方程方程的解。如下式（右边式子表示矩阵）：

　　那么我们是求y的最小值吗，不是的，我们要求WX+b和真实的y的值更加接近，这才是我们优化的目标。因此我们是求loss的最小值，（新的函数叫loss函数）当loss取得最小值的时候，[W,b]才是我们要求解的。如下图，红色直线即为我们要求的目标，它可以使总体的误差最小。

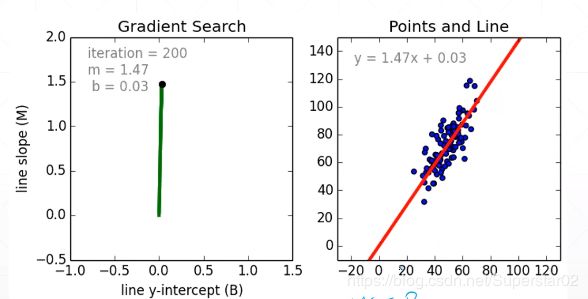
补充：
@Linear Regression: 即上面所讲问题，其中y∈（-∞，+∞），也就是说要预测的值就是连续的值。
@Logistic Regression：是在原来的Linear Regression加了一个激活函数，使得y∈（0,1），即一个概率的值，指的是当前的点概率为0到1，而不需要所有概率相加为1。
@Classification：分类问题，比如0~9手写数字，有十个点，每个点代表当前概率的大小，所有概率加起来等于1，即∑Pi = 1

实战Linear Regression

1. 计算总的loss function：
   
   实战代码如下，即可得到总的error

#定义一个计算总的error（即总的loss），其中points为一系列的（x，y）的组合:
def compute_error_for_line_given_points(b, w, points):
    totalError = 0      				#定义总的loss
    for i in range(0, len(points)):
        x = points[i, 0]  				#取该点的x值
        y = points[i, 1]  				#取该点的y值
        totalError += (y - (w * x + b)) ** 2 		#将每一个点的loss累加
    return totalError / float(len(points))			#对总的error求一个平均，返回总的平均error

2. 计算其梯度信息：
   
   实战代码如下，即可得到每一个的梯度信息

#定义一个计算梯度的函数：入口参数：b当前值，W当前值，点集合，学习率
def step_gradient(b_current, w_current, points, learningRate):
    b_gradient = 0
    w_gradient = 0
    N = float(len(points))      #总的数据点的个数
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        #∂L/∂b = 2（Wx + b - y），所有梯度累加时除以N，以便结果不用再做平均
        b_gradient += -(2/N) * (y - ((w_current * x) + b_current))
        #∂L/∂W = 2（Wx + b - y）x，所有梯度累加时除以N，以便结果不用再做平均
        w_gradient += -(2/N) * x * (y - ((w_current * x) + b_current))
    new_b = b_current - (learningRate * b_gradient)
    new_W = w_current - (learningRate * w_gradient)
    return [new_b, new_w]

3. 循环迭代梯度信息：

#循环迭代W，b，入口参数：（x，y）点集合，初始b,初始W，学习率，迭代次数：
def gradient_descent_runner(points, starting_b, starting_w, learning_rate, num_iterations):
    b = starting_b
    w = starting_w
    for i in range(num_iterations):
        b, w = step_gradient(b, w, np.array(points), learning_rate) 	#np.array（point）为（x，y）的数组
    return [b, w]

4. 总函数，先用num随机生成100个点（考虑实际观察带有噪声），100个点为文件data.csv。

def run():
    points = np.genfromtxt("data.csv", delimiter=",")       #取数据
    learning_rate = 0.0001
    initial_b = 0 # initial y-intercept guess
    initial_w = 0 # initial slope guess
    num_iterations = 1000
    print("Starting gradient descent at b = {0}, w = {1}, error = {2}"
          .format(initial_b, initial_w,
                  compute_error_for_line_given_points(initial_b, initial_w, points))
          )
    print("Running...")
    [b, w] = gradient_descent_runner(points, initial_b, initial_w, learning_rate, num_iterations)
    print("After {0} iterations b = {1}, m = {2}, error = {3}".
          format(num_iterations, b, w,
                 compute_error_for_line_given_points(b, w, points))
          )

if __name__ == '__main__':
    run()

推荐阅读：

PyTorch入门实战教程（一）：配置开发环境
PyTorch入门实战教程笔记（二）：简单回归问题