神经网络BP算法整理（1）
参考了若干blog文章，整理了BP算法的过程如下。
1网络参数
1.1网络结构
三层网络结构，输入层具有三个节点，隐含层也是三个节点，输出层两个节点。
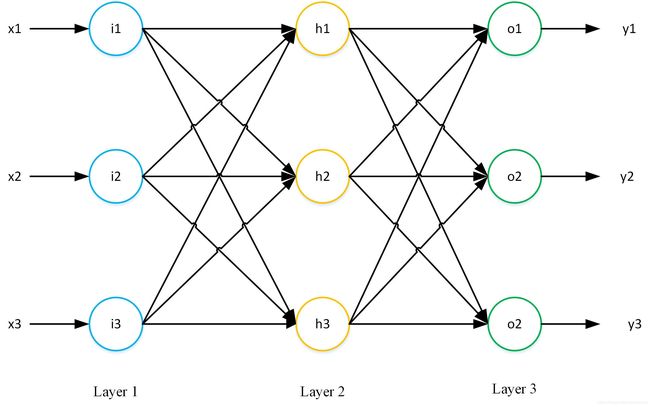节点也即为神经元，具有对各个连接线上的数据进行求和，并进行非线性变换（激活函数 f f f）的作用。
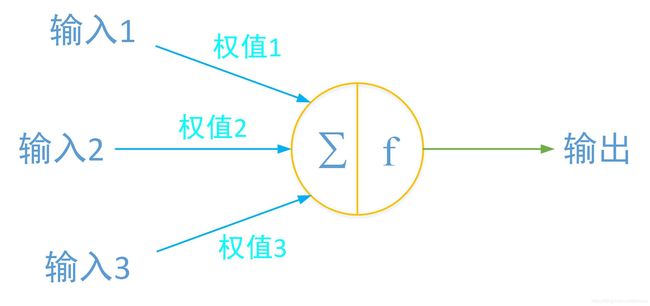
用上标 l l l代表层数， l = i , h , o l=i,h,o l=i,h,o分别代表输入层、隐含层和输出层，下标代表同一层中神经元的序号；
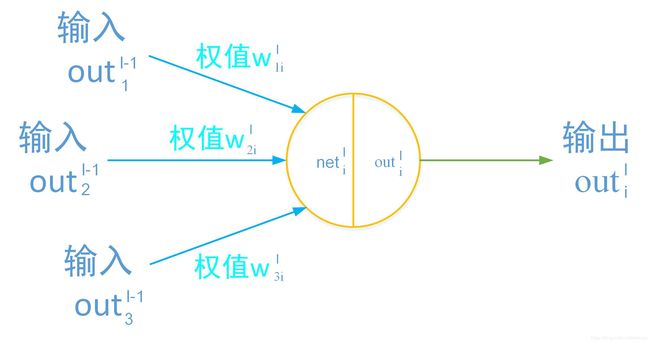
n e t i l net^l_i netil、 o u t i l out^l_i outil分别代表第 l l l层的第个 i i i神经元的输入和输出。
1.2参数初始化
采用如下的网络结构：
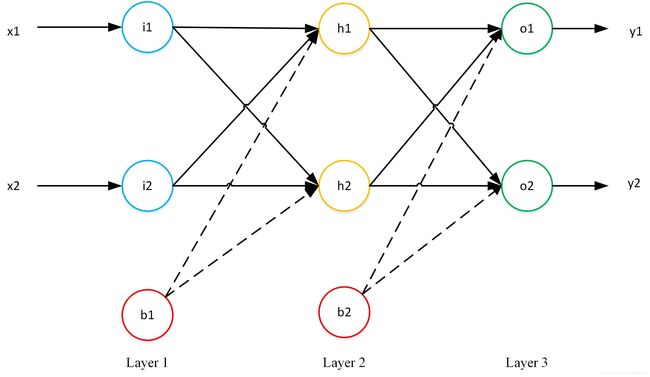
输入： x = [ 0.05 , 0.10 ] x=[0.05,0.10] x=[0.05,0.10]
理论输出： y = [ 0.01 , 0.99 ] y = [0.01,0.99] y=[0.01,0.99]
权重: w h = [ w 11 h w 12 h w 21 h w 22 h ] = [ 0.15 0.25 0.20 0.30 ] w^h= \left[ \begin{array}{ccc} w^h_{11} & w^h_{12} \\\\ w^h_{21} & w^h_{22} \\ \end{array} \right] =\left[ \begin{array}{ccc} 0.15 & 0.25 \\\\ 0.20 & 0.30 \\ \end{array} \right] wh=⎣⎡w11hw21hw12hw22h⎦⎤=⎣⎡0.150.200.250.30⎦⎤
w o = [ w 11 o w 12 o w 21 o w 22 o ] = [ 0.40 0.50 0.45 0.55 ] w^o= \left[ \begin{array}{ccc} w^o_{11} & w^o_{12} \\\\ w^o_{21} & w^o_{22} \\ \end{array} \right] =\left[ \begin{array}{ccc} 0.40 & 0.50 \\\\ 0.45 & 0.55\\ \end{array} \right] wo=⎣⎡w11ow21ow12ow22o⎦⎤=⎣⎡0.400.450.500.55⎦⎤
偏置:
b h = [ b 1 h b 2 h ] = [ 0.35 0.35 ] b^h= \left[ \begin{array}{ccc} b^h_{1}\\\\ b^h_{2} \\ \end{array} \right] =\left[ \begin{array}{ccc} 0.35 \\\\ 0.35\\ \end{array} \right] bh=⎣⎡b1hb2h⎦⎤=⎣⎡0.350.35⎦⎤
b o = [ b 1 o b 2 o ] = [ 0.60 0.60 ] b^o= \left[ \begin{array}{ccc} b^o_{1}\\\\ b^o_{2} \\ \end{array} \right] =\left[ \begin{array}{ccc} 0.60 \\\\ 0.60\\ \end{array} \right] bo=⎣⎡b1ob2o⎦⎤=⎣⎡0.600.60⎦⎤
激活函数采用sigmoid函数：
f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1
对其求导： f ( x ) ′ = f ( x ) ∗ ( 1 − f ( x ) ) f(x)'=f(x)*(1-f(x)) f(x)′=f(x)∗(1−f(x))
损失函数(loss function）,也即误差函数,设其为 g ( ∗ ) g(*) g(∗)：
采用平方差均值函数： E = g ( o u t o ) = 1 2 ∑ ( y − o u t o ) 2 E=g(out^o)=\frac{1}{2}{\sum(y-out^o)^2} E=g(outo)=21∑(y−outo)2对其求导: g ( o u t i o ) ′ = − ( y − o u t i o ) g(out^o_i)'=-(y-out^o_i) g(outio)′=−(y−outio)
学习率： η = 0.5 \eta = 0.5 η=0.5
1.3前馈网络（feedforward）
输入层
o u t 1 i = n e t 1 i = x 1 = 0.05 , o u t 2 i = n e t 2 i = x 2 = 0.10 out^i_1=net^i_1=x_1=0.05,\\out^i_2=net^i_2=x_2=0.10 out1i=net1i=x1=0.05,out2i=net2i=x2=0.10
隐藏层
（1）输入：
n e t i h = ∑ ( w j i h ∗ x j ) + b i h net^h_i=\sum(w^h_{ji}*x_j)+b^h_i netih=∑(wjih∗xj)+bih
（2）输出：
o u t i h = f ( n e t i h ) out^h_i=f(net^h_i) outih=f(netih)
输出层
（1）输入：
n e t i o = ∑ ( w j i o ∗ o u t j h + b i o ) net^o_i=\sum(w^{o}_{ji}*out^h_j+b^o_i) netio=∑(wjio∗outjh+bio)
（2）输出：
o u t i h = f ( n e t i h ) out^h_i=f(net^h_i) outih=f(netih)
1.4 误差反向传输（backpropagation）
反向传输是为了通过梯度下降的方法来更新权重参数：
w j i l = w j i l − η ∂ E ∂ w j i l w^l_{ji}=w^l_{ji}-\eta\frac{\partial E}{\partial w^l_{ji}} wjil=wjil−η∂wjil∂E b i l = b i l − η ∂ E ∂ b i l b^l_i =b^l_i-\eta\frac{\partial E}{\partial b^l_{i}} bil=bil−η∂bil∂E
采用链式法则，其中
对于输出层有：
∂ n e t i o ∂ w j i o = ∂ ∑ ( w j i o ∗ o u t j h ) + b i o ∂ w j i o = o u t j h \frac{\partial net^o_i }{\partial w^o_{ji}} = \frac{\partial \sum(w^o_{ji}*out^h_j)+b^o_i}{\partial w^o_{ji}} = out^h_j ∂wjio∂netio=∂wjio∂∑(wjio∗outjh)+bio=outjh ∂ n e t i o ∂ b i o = ∂ ∑ ( w j i o ∗ o u t j h ) + b i o ∂ b i o = 1 \frac{\partial net^o_i }{\partial b^o_{i}}=\frac{\partial \sum(w^o_{ji}*out^h_j)+b^o_i}{\partial b^o_{i}}=1 ∂bio∂netio=∂bio∂∑(wjio∗outjh)+bio=1
对于隐含层有：
∂ n e t i h ∂ w j i h = ∂ ∑ ( w j i h ∗ o u t j i ) + b i h ∂ w j i h = o u t j i = n e t j i = x j \frac{\partial net^h_i }{\partial w^h_{ji}} = \frac{\partial \sum(w^h_{ji}*out^i_j)+b^h_i}{\partial w^h_{ji}} = out^i_j=net^i_j=x_j ∂wjih∂netih=∂wjih∂∑(wjih∗outji)+bih=outji=netji=xj ∂ n e t i h ∂ b i h = ∂ ∑ ( w j i h ∗ o u t j i ) + b i h ∂ b i h = 1 \frac{\partial net^h_i }{\partial b^h_{i}}=\frac{\partial \sum(w^h_{ji}*out^i_j)+b^h_i}{\partial b^h_{i}}=1 ∂bih∂netih=∂bih∂∑(wjih∗outji)+bih=1
可得：
(1)对 w j i o w^o_{ji} wjio进行求偏导
∂ E ∂ w j i o = ∂ E ∂ o u t i o ∂ o u t i o ∂ n e t i o ∂ n e t i o ∂ w j i o \frac{\partial E}{\partial w^o_{ji}}=\frac{\partial E}{\partial out^o_i}\frac{\partial out^o_i}{\partial net^o_i}\frac{\partial net^o_i}{\partial w^o_{ji}} ∂wjio∂E=∂outio∂E∂netio∂outio∂wjio∂netio = g ( x ) ′ ∣ x = o u t i o f ( x ) ′ ∣ x = n e t i o o u t j h =g(x)'|_{x=out^o_i}f(x)'|_{x=net^o_{i}}out^h_j =g(x)′∣x=outiof(x)′∣x=netiooutjh
(2)对 b i o b^o_{i} bio进行求偏导
∂ E ∂ b i o = ∂ E ∂ o u t i o ∂ o u t i o ∂ n e t i b ∂ n e t i o ∂ w j i o = g ( x ) ′ ∣ x = o u t i o f ( x ) ′ ∣ x = n e t i o \frac{\partial E}{\partial b^o_{i}}=\frac{\partial E}{\partial out^o_i}\frac{\partial out^o_i}{\partial net^b_i}\frac{\partial net^o_i}{\partial w^o_{ji}}\\ =g(x)'|_{x=out^o_i}f(x)'|_{x=net^o_{i}} ∂bio∂E=∂outio∂E∂netib∂outio∂wjio∂netio=g(x)′∣x=outiof(x)′∣x=netio
(3)对 w j i h w^h_{ji} wjih进行求偏导
∂ E ∂ w j i h = ∂ E ∂ o u t i h ∂ o u t i h ∂ n e t i h ∂ n e t i h ∂ w j i h \frac{\partial E}{\partial w^h_{ji}}=\frac{\partial E}{\partial out^h_i}\frac{\partial out^h_i}{\partial net^h_i}\frac{\partial net^h_i}{\partial w^h_{ji}} ∂wjih∂E=∂outih∂E∂netih∂outih∂wjih∂netih = ∂ E ∂ o u t i h f ( x ) ′ ∣ x = n e t i h o u t j i =\frac{\partial E}{\partial out^h_i}f(x)'|_{x=net^h_{i}}out^i_j =∂outih∂Ef(x)′∣x=netihoutji
其中 ∂ E ∂ o u t i h = ∑ n = 1 N h ∂ E ∂ o u t n o ∂ o u t n o ∂ n e t n o ∂ n e t n o ∂ o u t i h \frac{\partial E}{\partial out^h_i}=\sum^{N_h}_{n=1}\frac{\partial E}{\partial out^o_n}\frac{\partial out^o_n}{\partial net^o_n}\frac{\partial net^o_n}{\partial out^h_i } ∂outih∂E=n=1∑Nh∂outno∂E∂netno∂outno∂outih∂netno
o u t j i = n e t j i = x j out^i_j=net^i_j=x_j outji=netji=xj
其中 ∂ E ∂ o u t n o = g ( x ) ′ ∣ x = o u t n o \frac{\partial E}{\partial out^o_n}= g(x)'|_{x=out^o_n} ∂outno∂E=g(x)′∣x=outno
∂ o u t n o ∂ n e t n o = f ( x ) ′ ∣ x = n e t n o \frac{\partial out^o_n}{\partial net^o_n} = f(x)'|_{x=net^o_{n}} ∂netno∂outno=f(x)′∣x=netno
∂ n e t n o ∂ o u t i h = ∂ ∑ m = 1 N h ( w m n o ∗ o u t m h ) + b n o ∂ o u t i h = w i n o \frac{\partial net^o_n}{\partial out^h_i }={\frac{\partial \sum^{N_h}_{m=1}(w^o_{mn}*out^h_m)+b^o_n}{\partial out^h_{i}}}=w^o_{in} ∂outih∂netno=∂outih∂∑m=1Nh(wmno∗outmh)+bno=wino
于是 ∂ E ∂ w j i h = ∑ n = 1 N h [ g ( x ) ′ ∣ x = o u t n o f ( x ) ′ ∣ x = n e t n o w i n o ] f ( x ) ′ ∣ x = n e t i h o u t j i \frac{\partial E}{\partial w^h_{ji}}=\sum^{N_h}_{n=1}[g(x)'|_{x=out^o_n}\ f(x)'|_{x=net^o_{n}}\ w^o_{in}] f(x)'|_{x=net^h_{i}}\ out^i_j ∂wjih∂E=n=1∑Nh[g(x)′∣x=outno f(x)′∣x=netno wino]f(x)′∣x=netih outji
其中 N h N_h Nh为 h h h层(hidden，隐藏层)的神经元节点的个数。
(4)对 b i h b^h_{i} bih进行求偏导
∂ E ∂ b i h = ∂ E ∂ o u t i h ∂ o u t i h ∂ n e t i h ∂ n e t i h ∂ b i h \frac{\partial E}{\partial b^h_i} =\frac{\partial E}{\partial out^h_i}\frac{\partial out^h_i}{\partial net^h_i}\frac{\partial net^h_i}{\partial b^h_i} ∂bih∂E=∂outih∂E∂netih∂outih∂bih∂netih
参考（3）可得：
∂ E ∂ b i n = ∑ n = 1 N h [ g ( x ) ′ ∣ x = o u t n o f ( x ) ′ ∣ x = n e t n o w i n o ] f ( x ) ′ ∣ x = n e t i h \frac{\partial E}{\partial b^n_i}= \sum^{N_h}_{n=1}[g(x)'|_{x=out^o_n}\ f(x)'|_{x=net^o_{n}}\ w^o_{in}] f(x)'|_{x=net^h_{i}} ∂bin∂E=n=1∑Nh[g(x)′∣x=outno f(x)′∣x=netno wino]f(x)′∣x=netih
考虑到同一层的权重与偏置的导数的相似之处，整理得：
∂ E ∂ w j i o = δ i o o u t j h \frac{\partial E}{\partial w^o_{ji}}= \delta^o_{i}out^h_j ∂wjio∂E=δiooutjh
∂ E ∂ b i o = δ i o \frac{\partial E}{\partial b^o_{i}}= \delta^o_i ∂bio∂E=δio
∂ E ∂ w j i h = δ i h o u t j i = δ i h x j \frac{\partial E}{\partial w^h_{ji}}=\delta^h_{i}out^i_j\ = \delta^h_{i}x_j ∂wjih∂E=δihoutji =δihxj
∂ E ∂ b i o = δ i h \frac{\partial E}{\partial b^o_{i}}= \delta^h_i ∂bio∂E=δih其中的 δ i h 、 δ i o \delta^h_i、\delta^o_i δih、δio分别是隐含层和输出层的误差项：
δ i o = g ( x ) ′ ∣ x = o u t i o f ( x ) ′ ∣ x = n e t i o \delta^o_i=g(x)'|_{x=out^o_i}f(x)'|_{x=net^o_{i}} δio=g(x)′∣x=outiof(x)′∣x=netio
δ i h = ∑ n = 1 N h [ g ( x ) ′ ∣ x = o u t n o f ( x ) ′ ∣ x = n e t n o w i n o ] f ( x ) ′ ∣ x = n e t i h \delta^h_i= \sum^{N_h}_{n=1}[g(x)'|_{x=out^o_n}\ f(x)'|_{x=net^o_{n}}\ w^o_{in}] f(x)'|_{x=net^h_{i}} δih=n=1∑Nh[g(x)′∣x=outno f(x)′∣x=netno wino]f(x)′∣x=netih由上述两个公式可得： δ i h = ∑ n = 1 N h [ δ n o w i n o ] f ( x ) ′ ∣ x = n e t i h \delta^h_i=\sum^{N_h}_{n=1}[\delta^o_n\ w^o_{in}]f(x)'|_{x=net^h_{i}} δih=n=1∑Nh[δno wino]f(x)′∣x=netih
可知，隐含层的误差项为输出层的误差项与两层之间的权重的乘积的求和，再乘以在该节点输入处的激活函数的导数。
当有多个隐含层时，也具有相同的特点，即： l l l层的误差项 δ l \delta^l δl与 l + 1 l+1 l+1 层的误差项 δ l + 1 \delta^{l+1} δl+1之间有如下关系： δ i l = ∑ n = 1 N l [ δ n l + 1 w i n l + 1 ] f ( x ) ′ ∣ x = n e t i l \delta^l_i=\sum^{N_l}_{n=1}[\delta^{l+1}_nw^{l+1}_{in}]f(x)'|_{x=net^l_i} δil=n=1∑Nl[δnl+1winl+1]f(x)′∣x=netil
代入本案例的网络中的误差函数和激活函数，到此便可对权重和偏置进行更新：
w j i o = w j i o − η ∂ E ∂ w j i o w^o_{ji} = w^o_{ji} - \eta\frac{\partial E}{\partial w^o_{ji}} wjio=wjio−η∂wjio∂E
b i o = b i o − η ∂ E ∂ b i o b^o_{i} = b^o_{i} - \eta\frac{\partial E}{\partial b^o_{i}} bio=bio−η∂bio∂E
w j i h = w j i h − η ∂ E ∂ w j i h w^h_{ji} = w^h_{ji} - \eta\frac{\partial E}{\partial w^h_{ji}} wjih=wjih−η∂wjih∂E
b i o = b i o − η ∂ E ∂ b i o b^o_{i} = b^o_{i} - \eta\frac{\partial E}{\partial b^o_{i}} bio=bio−η∂bio∂E
参考：
1.【1】【深度学习】神经网络入门（最通俗的理解神经网络）2018-01-06 这个转自3
【2】这个贴的标签是原创2019-05-11
【3】这个已经失效
2
【1】cnblog，Alex，BP神经网络推导过程详解，
3 【1】csdn,磐创 AI,一文彻底搞懂BP算法：原理推导+数据演示+项目实战（上篇）