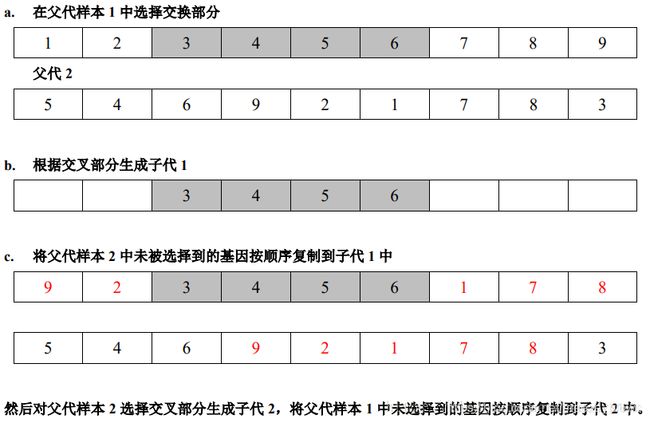
用遗传算法求解旅行商问题
以下是用遗传算法解决旅行商问题的实验报告
1.问题描述
旅行商问题(Travelling Salesman Problem, 简记TSP,亦称货郎担问题):设有n个城市和距离矩阵D=[dij],其中dij表示城市i到城市j的距离,i,j=1,2 … n,则问题是要找出遍访每个城市恰好一次的一条回路并使其路径长度为最短。
2.算法设计
遗传算法(GeneticAlgorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,通过模拟自然进化过程搜索最优解。遗传算法是从首先是初始化一个种群,然后根据适应性函数确定个体的适应度,由适应度来选择个体进行交叉,以某种概率让个体进行变异,从而不断选出适应度高的个体,进而更新种群。
算法流程图如下图所示。
其中
(1)城市个数选择中国34个省会城市坐标,种群规模设置为100,变异概率设置为0.01,迭代次数初步设置为5000。
(2)个体适应度代表的是34个城市连成路线的欧式距离。
(3)选择个体进行交叉操作的时候采用轮盘赌策略。
qa 表示个体a的累积概率,如上图所示个体1、2、3、4的累积概率分别为0.14、0.53、0.6,1。随机生成一个0到1的浮点数f,若 qa < f <= qb,则个体b被选中。当采用轮盘赌策略选择交叉父体之后,采用顺序交叉法进行交叉操作:
(3)变异操作对每一个个体以变异概率确定是否变异,如果变异的话,随机在个体中选择两个城市,然后交换这两个城市的位置得到变异的效果。
(4)产生新的个体之后,采用精英保留策略,即适应度最好的20个体会被保留下来,其他个体按照适应度进行保留。
3.程序流程
1.初始化城市序列的坐标
2.用欧式距离计算城市序列中每个个体的适应度
3.根据适应度来选择个体作为交叉操作的父体,选择完之后用顺序交叉来进行交叉操作
4.以一定的变异个体才确定是否对个体进行变异,如果需要进行变异,侧随机选择个体的两个城市进行交换。
5.选择适应度最好的20个个体直接保留到下一代,下一代的其他个体按照个体的适应度进行选择。
6.判断是否达到迭代次数,如果没有转到第2步,达到的话转到第7步。
7.输出适应度最好的个体。
4.代码
import numpy as np
import random
import copy
import matplotlib.pyplot as plt
class City:
def __init__(self, x, y):
self.x = x
self.y = y
def __repr__(self):
return "(" + str(self.x) + "," + str(self.y) + ")"
def distance(ca, cb):
dx = abs(ca.x - cb.x)
dy = abs(ca.y - cb.y)
distance = np.sqrt((dx ** 2) + (dy ** 2))
return distance
def init_pop(city_list, popSize):
pop = []
for i in range(popSize):
new_city_list = random.sample(city_list, len(city_list))
pop.append(new_city_list)
return pop
def fitness(pop):
dis_citys = distance_citys(pop)
return 1.0/dis_citys
def distance_citys(pop):
temp_dis = 0
for i in range(len(pop)-1):
temp_dis += distance(pop[i], pop[i+1])
temp_dis += distance(pop[len(pop)-1], pop[0])
return temp_dis
def rank(poplulation):
rankPop_dic = {}
for i in range(len(poplulation)):
fit = fitness(poplulation[i])
rankPop_dic[i] = fit
return sorted(rankPop_dic.items(), key=lambda x:x[1], reverse=True)
def select(pop, pop_rank, eliteSize):
select_pop = []
for i in range(eliteSize):
select_pop.append(pop[pop_rank[i][0]])
cumsum = 0
cumsum_list = []
temp_pop = copy.deepcopy(pop_rank)
for i in range(len(temp_pop)):
cumsum += temp_pop[i][1]
cumsum_list.append(cumsum)
for i in range(len(temp_pop)):
cumsum_list[i] /= cumsum
for i in range(len(temp_pop)-eliteSize):
rate = random.random()
for j in range(len(temp_pop)):
if cumsum_list[j] > rate:
select_pop.append(pop[pop_rank[i][0]])
break
return select_pop
def breed(pop, eliteSize):
breed_pop = []
for i in range(eliteSize):
breed_pop.append(pop[i])
i = 0
while i < (len(pop)-eliteSize):
a = random.randint(0, len(pop)-1)
b = random.randint(0, len(pop)-1)
if a != b:
fa, fb = pop[a], pop[b]
genea, geneb = random.randint(0, len(pop[a])-1), random.randint(0, len(pop[b])-1)
startgene = min(genea, geneb)
endgene = max(genea, geneb)
child1 = []
for j in range(startgene, endgene):
child1.append(fa[j])
# child1 = copy.deepcopy(fa[:-1])
child2 = []
for j in fb:
if j not in child1:
child2.append(j)
# child2 = [j for j in fb if j not in child1]
breed_pop.append(child1+child2)
i = i+1
return breed_pop
def mutate(pop, mutationRate):
mutation_pop = []
for i in range(len(pop)):
for j in range(len(pop[i])):
rate = random.random()
if rate < mutationRate:
a = random.randint(0, len(pop[i])-1)
pop[i][a], pop[i][j] = pop[i][j], pop[i][a]
mutation_pop.append(pop[i])
return mutation_pop
def next_pop(population, eliteSize, mutationRate):
pop_rank = rank(population) #按照适应度排序
select_pop = select(population, pop_rank, eliteSize) #精英选择策略,加上轮盘赌选择
breed_pop = breed(select_pop, eliteSize) #繁殖
next_generation = mutate(breed_pop, mutationRate) #变异
return next_generation
#画出路线图的动态变化
def GA_plot_dynamic(city_list, popSize, eliteSize, mutationRate, generations):
plt.figure('Map')
plt.ion()
population = init_pop(city_list, popSize)
print("initial distance:{}".format(1.0/(rank(population)[0][1])))
for i in range(generations):
plt.cla()
population = next_pop(population, eliteSize, mutationRate)
idx_rank_pop = rank(population)[0][0]
best_route = population[idx_rank_pop]
city_x = []
city_y = []
for j in range(len(best_route)):
city = best_route[j]
city_x.append(city.x)
city_y.append(city.y)
city_x.append(best_route[0].x)
city_y.append(best_route[0].y)
plt.scatter(city_x, city_y, c='r', marker='*', s=200, alpha=0.5)
plt.plot(city_x, city_y, "b", ms=20)
plt.pause(0.1)
plt.ioff()
plt.show()
print("final distance:{}".format(1.0 / (rank(population)[0][1])))
bestRouteIndex = rank(population)[0][0]
bestRoute = population[bestRouteIndex]
return bestRoute
def GA(city_list, popSize, eliteSize, mutationRate, generations):
population = init_pop(city_list, popSize) #初始化种群
process = []
print("initial distance:{}".format(1.0/(rank(population)[0][1])))
for i in range(generations):
population = next_pop(population, eliteSize, mutationRate) #产生下一代种群
process.append(1.0 / (rank(population)[0][1]))
plt.figure(1)
print("final distance:{}".format(1.0 / (rank(population)[0][1])))
plt.plot(process)
plt.ylabel('Distance')
plt.xlabel('Generation')
plt.savefig(str(generations)+ '_' + str(1.0 / (rank(population)[0][1])) + '_' + str(mutationRate) +'_process.jpg')
plt.figure(2)
idx_rank_pop = rank(population)[0][0]
best_route = population[idx_rank_pop]
city_x = []
city_y = []
for j in range(len(best_route)):
city = best_route[j]
city_x.append(city.x)
city_y.append(city.y)
city_x.append(best_route[0].x)
city_y.append(best_route[0].y)
plt.scatter(city_x, city_y, c='r', marker='*', s=200, alpha=0.5)
plt.plot(city_x, city_y, "b", ms=20)
plt.savefig(str(generations)+'_' + str(mutationRate) + '_route.jpg')
plt.show()
num_city = 25
city_list = []
# for i in range(num_city):
# x = random.randint(1, 200)
# y = random.randint(1, 200)
# city_list.append(City(x, y))
with open('city.txt', 'r', encoding='UTF-8') as f:
lines = f.readlines()
for line in lines:
line = line.replace('\n', '')
# line = line.replace('\t', '')
city = line.split('\t')
city_list.append( City( float(city[1]), float(city[2]) ) )
# mutationRates = [0.001, 0.002, 0.005, 0.008, 0.01, 0.02]
# for mut in mutationRates:
GA(city_list, 100, 20, 0.01, 5000)5.代码运行及测试
在城市个数即中国省会城市个数为34,种群大小为100,选择20个精英进行保留,采用轮盘赌选择交叉父体,顺序交叉方式进行交叉操作.
变异概率为0.01的情况下。对迭代次数500,800,1000,3000,5000,6000进行了测试。
根据实验结果可以看出,随着次数的增加,城市之间的路线距离也在逐渐的下降,而且可以发现,在迭代次数增加的前期,比如500增到100的时候,城市之间的距离下降的比较快,而在于迭代次数增加的后期比如5000-6000,距离基本没有明显的下降了,而是趋于平稳,可以证明本实验设计的算法大概在5000次左右就可以收敛到一个蛮好的结果。
最后,由于遗传算法是一个启发式的算法,存在一定的偶然性,有时候可能会陷入到一种局部最优解中,比如我在实验中有时候尝试次数为7000次的时候,效果反而没有之前的好。这也说明了并不是迭代次数越多越好。
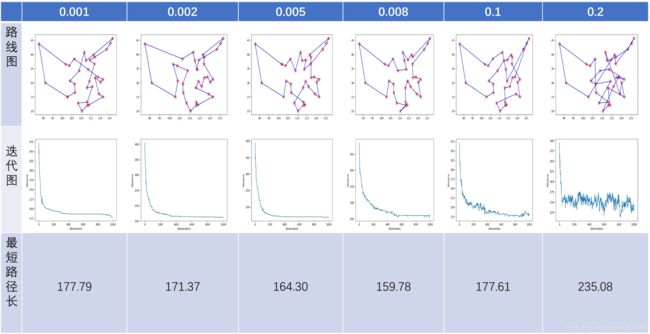
在迭代次数为1000的情况下,依次对变异率0.001,0.002,0.005,0.008,.0.01,0.02进行了测试:
根据实验结果可以看出,当变异率从0.001逐渐增大的时候,城市之间的路径连线在得到不断的优化,即最短路径长度逐渐变短。当变异率逐渐增大到0.008以后,进一步增大到0.1甚至0.2的时候发现路径反而变差了,即最短路径长度再次出现增大的情况,而且根据迭代曲线可以看出,在迭代的过程中出现了明显的震荡,证明了过高的变异率会导致遗传算法的不稳定性,从而使得算法陷入到了一个局部最优解中。
所以可以看出变异率对于遗传算法的最终效果显得尤为重要,过小或者过大都不是一种好的选择,根据实验结果0.008左右会是一个不错的参考值。
6.结论
旅行商问题属于NP难问题,无法在线性的复杂度中求解。利用遗传算法这种启发式算法可以在相对短的时间内找到一个相对优化的解。而且在实验中我们发现,一些超参数的设置,比较变异率,种群大小,迭代次数对于最终的结果都是至关重要的。另外对于一些策略,比如交叉策略,精英保留策略的运用对于产生一个好的解显得尤为重要。
参考:
https://zhuanlan.zhihu.com/p/41292727
https://blog.csdn.net/greedystar/article/details/80343841
附录:
程序中选择的数据为中国省会城市坐标
北京 116.46 39.92
天津 117.2 39.13
上海 121.48 31.22
重庆 106.54 29.59
拉萨 91.11 29.97
乌鲁木齐 87.68 43.77
银川 106.27 38.47
呼和浩特 111.65 40.82
南宁 108.33 22.84
哈尔滨 126.63 45.75
长春 125.35 43.88
沈阳 123.38 41.8
石家庄 114.48 38.03
太原 112.53 37.87
西宁 101.74 36.56
济南 117 36.65
郑州 113.6 34.76
南京 118.78 32.04
合肥 117.27 31.86
杭州 120.19 30.26
福州 119.3 26.08
南昌 115.89 28.68
长沙 113 28.21
武汉 114.31 30.52
广州 113.23 23.16
台北 121.5 25.05
海口 110.35 20.02
兰州 103.73 36.03
西安 108.95 34.27
成都 104.06 30.67
贵阳 106.71 26.57
昆明 102.73 25.04
香港 114.1 22.2
澳门 113.33 22.13