机器学习之数学系列（二）梯度下降法(参数更新公式的由来)
一、引言
下山问题
如下图所示，假设我们位于黄山的某个山腰处，山势连绵不绝，不知道怎么下山。于是决定走一步算一步，也就是每次选个方向往山下走一步，这样一步一步走下去，一直走到觉得我们已经到了山脚。问题是当我以一定的步长下坡时，我可以选择的方向有很多，到底选哪个方向最好呢？经验告诉我们选最陡的方向走，因为这样可以快速下山。那具体的最陡的方向是哪个方向？答案是：梯度的负方向。本文的工作有1.阐述为什么下坡最陡的方向即对于凸函数而言值变小最快的方向是梯度的反方向。2.给出梯度下降法中的参数更新公式。3.解释为啥不直接求导而要用梯度下降法。4.给出梯度下降法代码示例。
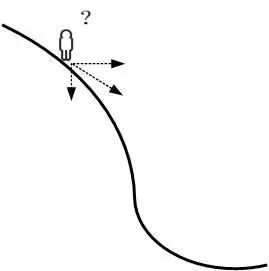
二、梯度下降法
什么是梯度？通俗来说，梯度就是表示函数值变化最快的方向，即： ∇ f ( θ ⃗ ) = ( ∂ f ∂ θ 1 , ∂ f ∂ θ 2 , . . . , ∂ f ∂ θ n ) ， 其 中 θ ⃗ = ( θ 1 , θ 2 , . . . , θ n ) \nabla f(\vec{\theta})=(\frac{\partial f}{\partial\theta_1},\frac{\partial f}{\partial\theta_2},...,\frac{\partial f}{\partial\theta_n})，其中\vec{\theta}=(\theta_1,\theta_2,...,\theta_n) ∇f(θ)=(∂θ1∂f,∂θ2∂f,...,∂θn∂f)，其中θ=(θ1,θ2,...,θn)
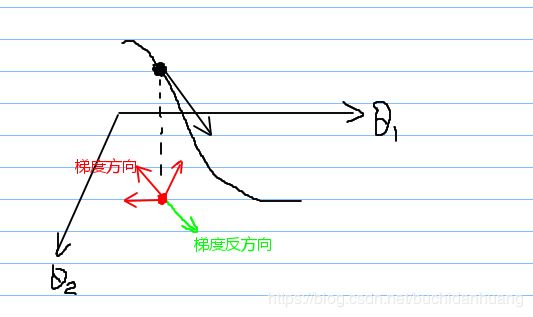如上图所示，红点为参数点，红色点对应的函数值为黑色点值，当红色点沿着某一方向移动时函数值将跟随变化。很明显参数更新公式就应当是 θ ⃗ c u r = θ ⃗ p r e + η v ⃗ \vec \theta_{cur}=\vec \theta_{pre}+\eta \vec v θcur=θpre+ηv，其中 η \eta η是参数点移动的步长(各方向的合步长)， v ⃗ \vec v v是参数更新单位方向向量。根据图像我们发现只能沿着某些方向才能使得函数值往小了变化，例如与梯度方向呈钝角的所有方向都可以，进一步的我需要考虑的是哪个方向能使得函数值变小最快。
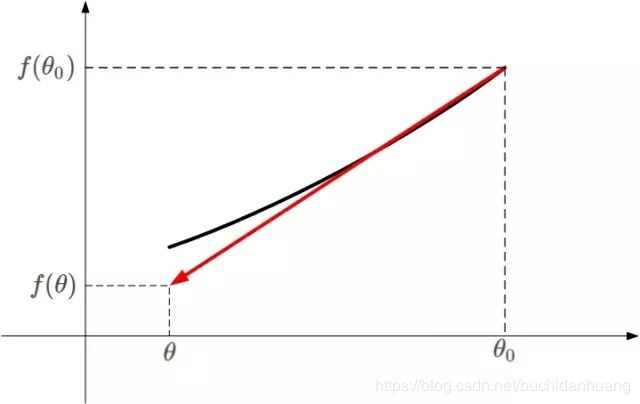
以一维函数为例说明函数变小最快的方向。如上图所示，凸函数 f ( θ ) f(θ) f(θ)的某一小段[ θ θ θ, θ 0 θ_0 θ0]由上图黑色曲线表示，可以利用线性近似的思想求出 f ( θ ) f(θ) f(θ)的值即：当步长很小时，曲线近似于红色斜直线。红色直线的斜率等于 f ( θ ) f(θ) f(θ)在 θ 0 θ_0 θ0处的导数。则根据直线方程，很容易得到 f ( θ ) f(θ) f(θ)的近似表达式为： f ( θ ) ≈ f ( θ 0 ) + ( θ − θ 0 ) ∇ f ( θ 0 ) f(\theta)\approx f(\theta_0)+(\theta-\theta_0)\nabla f(\theta_0) f(θ)≈f(θ0)+(θ−θ0)∇f(θ0)
这也是一阶泰勒展开式的推导过程，主要利用的数学思想就是曲线函数的线性拟合近似。
根据多维的参数更新公式这里的一维参数更新公式应当为： θ − θ 0 = η v ⃗ \theta-\theta_0=\eta \vec v θ−θ0=ηv带入一阶泰勒展开式： f ( θ ) ≈ f ( θ 0 ) + η v ⃗ ∇ f ( θ 0 ) f(\theta)\approx f(\theta_0)+\eta \vec v\nabla f(\theta_0) f(θ)≈f(θ0)+ηv∇f(θ0)
我们在凸函数上是希望通过逐步下降方式来求得最小值，故而希望， f ( θ ) < f ( θ 0 ) f(\theta)
从这个公式可知要使得函数值往小了变，参数更新方向必须和梯度方向是呈钝角的。 f ( θ ) − f ( θ 0 ) f(\theta)-f(\theta_0) f(θ)−f(θ0)要想获得最大值(负最大)，即要求参数更新方向 v ⃗ \vec v v和 ∇ f ( θ 0 ) \nabla f(\theta_0) ∇f(θ0)方向相反即可。实际上无论凸函数还是凹函数，沿着当前点的梯度方向的反方向更新参数，它会往函数的极值点走并且这个方向是最快方向。
三、参数更新公式
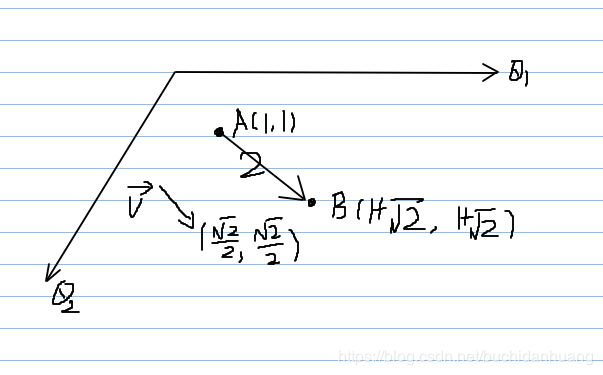如图所示：从点A(1,1)沿着 v ⃗ \vec v v( 2 2 \frac{\sqrt2}{2} 22, 2 2 \frac{\sqrt2}{2} 22)方向移动2个单位到达点B(1+ 2 \sqrt2 2, 1+ 2 \sqrt2 2)，那么A、B两点的关系是什么？应该是 B ⃗ \vec B B= A ⃗ \vec A A+2* v ⃗ \vec v v。由此可以得出一般的参数的更新公式是：
θ ⃗ c u r = θ ⃗ p r e + η v ⃗ \vec \theta_{cur}=\vec \theta_{pre}+\eta \vec v θcur=θpre+ηv，其中 η \eta η是参数移动的步长， v ⃗ \vec v v是参数更新单位方向向量。参数更新公式一定要带单位方向，如果只有步长那么将不知道参数是往哪个方向更新的，在一维的情况下我们会根据图像来看是 + η +\eta +η还是 − η -\eta −η，符号即单位方向向量。如何确定更新方向？其实更新方向基本的就一个要求即：使得函数值变大或变小，例如二维凸函数求最小值时与梯度方向呈钝角的所有方向都可以，之所以最终确定的是与梯度呈180度角的方向(即反方向)是因为那个方向既可以使得函数值变小又保证了变小最快；在一维凸函数中，要想使得函数值变小它只有一个方向，只能取那个方向来更新参数。如果 v ⃗ \vec v v取梯度的反方向那么即： v ⃗ = − ∇ f ( θ 0 ) ∣ ∣ ∇ f ( θ 0 ) ∣ ∣ \vec v=-\frac{\nabla f(\theta_0)}{||\nabla f(\theta_0)||} v=−∣∣∇f(θ0)∣∣∇f(θ0)，那么便得到了常用的参数更新公式： θ ⃗ c u r = θ ⃗ p r e − η ∇ f ( θ 0 ) ∣ ∣ ∇ f ( θ 0 ) ∣ ∣ \vec \theta_{cur}=\vec \theta_{pre}-\eta\frac{\nabla f(\theta_0)}{||\nabla f(\theta_0)||} θcur=θpre−η∣∣∇f(θ0)∣∣∇f(θ0)
将分母合并进步长表达为更一般形式： θ ⃗ c u r = θ ⃗ p r e − η ∇ f ( θ 0 ) \vec \theta_{cur}=\vec \theta_{pre}-\eta\nabla f(\theta_0) θcur=θpre−η∇f(θ0)负梯度值表明了参数更新的方向，这个公式隐式的增大了步长，故而要把步长设小一点。
参数更新方向不一定非得是梯度的反方向，还可能是其他方向，例如为了跳出鞍点，往往不再选择梯度反方向而是考虑其他更合适的方向，有兴趣的可以去了解一下Momentum、RMSprop、Adam优化算法的参数更新公式，看看它们是如何考虑参数更新方向的。
梯度下降法需把握以下两点：
1.参数更新公式是什么 。
2.梯度如何计算，这需要函数矩阵求导和链式法则的知识。
四、为什么要用梯度下降法
为什么不直接求出导数，然后令导数为0，然后解方程获得极值点的参数值，而要去用梯度下降法来逐步逼近求？原因是：
1.梯度为0的方程不一定能解出来，但是我们计算梯度的值是可以算的
2.以线性回归为例通过代价函数对参数求导，令其为零，得出参数为：
参数的结果给出两个信息，同时也是直接求导不可行的原因：
X的转置乘以X必须要可逆，也就是X必须可逆，但是实际情况中并不一定都满足这个条件，因此直接求导不可行；假设可逆，那么就需要去求X的转置乘以X这个整体的逆，线性代数中给出了求逆矩阵的方法，是非常复杂的(对计算机来说就是十分消耗性能的)，数据量小时，还可行，一旦数据量大，计算机求矩阵的逆将会是一项非常艰巨的任务，消耗的性能以及时间巨大，而在机器学习中，数据量少者上千，多者上亿；因此直接求导不可行。相较而言，梯度下降算法同样能够实现最优化求解，通过多次迭代使得代价函数收敛，并且使用梯度下降的计算成本很低，所以基于以上两个原因，回归中多数采用梯度下降而不是求导等于零来求参数。
五、梯度下降法示例
#example1
def grad_descent(n, initx, lambd=0.01):
"""
Q:随机给一个值n,估算x,使得x**2=n
A:令f(x) = x**2 - n,f(x)趋于0时的x即为所求,用梯度下降法逼近求解
"""
x = initx
fx = x**2 - n
while fx>0:#结束条件可以是迭代次数也可以是某个指标的值达到阈值
fx = x**2 - n
print(fx)
x -= lambd*2*x
return float(format(x, '.2f'))
print(grad_descent(4.0, -5.9, 0.001))
#example2
import numpy as np
class LogisticRegression(object):
# W = np.zeros((1,dim)), b = 0
def __init__(self, W, b):
self.W = W
self.b = b
def forward(self, X, Y):
grad = {}
dim, m = X.shape
O = np.array([1 for _ in range(m)])
Z = np.dot(self.W, X) + self.b
A = 1 / (1 + np.exp(-Z))
loss = 1/m * np.dot((-Y * np.log(A) - (O-Y)*np.log(O-A)), O.T)
dw = 1/m * np.dot(A-Y, X.T)
db = 1/m * np.dot(A-Y, O.T)
grad['dw'] = dw
grad['db'] = db
return grad, loss
def fit(self, X, Y, lambd, iteration_num):
params = {}
for i in range(iteration_num):
grad, loss = self.forward(X,Y)
dw = grad['dw']
db = grad['db']
self.W = self.W - lambd * dw
self.b = self.b - lambd * db
if i % 10==0:
print('iter {0}, loss:{1}'.format(i, float(loss)))
params['W'] = self.W
params['b'] = self.b
return params
def predict(self, x):
Z = np.dot(self.W, X) + self.b
A = 1 / (1 + np.exp(-Z))
return A
lr = LogisticRegression(np.zeros((1,2)), 0)
X = np.array([[1.,2.,-1.],[3.,4.,-3.2]])
Y = np.array([[1,0,1]])
print(lr.fit(X, Y, 0.1, 1000))
参考：