【原创】树状数组 单点修改区间修改单点查询区间查询 逆序对 二维偏序 （未完成）

BIT

Preface

数据结构学复习Part 1。

lowbit

一个重要的函数是lowbit(x)，能算出x的二进制中最后一位的1是哪一位的1,如果是第k位的就返回$2^{k-1}$。
比方说$(5{)}_{10}=(101{)}_2,lowbit(5)=1$，$(8{)}_{10}=(1000{)}_2,lowbit(8)=8$，$(27{)}_{10}=(11011{)}_2,lowbit(27)=1$，$(24{)}_{10}=(11000{)}_2,lowbit(24)=8$。

发现计算机存负数的二进制的方法，补码，一个数的补码是它的反码+1，反码就是每一位都取反。比如说：$$\begin{gathered} 原码000111001011100 \\ 反码111000110100011 \\ 补码111000110100100 \end{gathered}$$
发现反码的一个数最后一位的1及其之后的一串0反转为$011111111111\cdots$，然后+1就又会变回去$，100000000000$。所以我们把一个数和它的相反数$\&$起来，最后一个1之前的数都被反转过了，所以必然是0，而最后一个1及其之后是一样的，所以结果必然是我们要求的东西。

语文太差了，没办法描述清楚。

单点修改区间查询

从动态维护区间和开始

如题，我们要动态维护区间和。
不动态怎么做？
$(线段树！！)$
我们就维护一个前缀和数组，$S[i]=S[i-1]+arr[i]$，然后区间$[l,r]$的和就是$S[r]-S[l-1]$。

动态是什么意思？$arr$会变！
那你更新了$arr[i]$我就修改$S[i],S[i+1],\cdots ,S[n]$呗。
这样每次修改的时间复杂度是$\Theta (n)$的，不采纳。

于是我们看了看快速幂算法，就想把这n次拆成二进制的形式换成$lo{g}_{2}n$次。
我们又拿来一个数组$C[n]$，吸取$S$数组的经验，重新定义。

---

为什么更新$sig$的时间复杂度是$\Theta (n)$的呢？因为我们的$S[i]$与$S[i-1]$挂钩，$S[i-1]$又与$S[i-2]$有关……。牵一发而动全身，其中一个值变了就会激起无限的化学反应。
那为什么我们要全身都动呢？因为这样可以$\Theta (1)$查询，查询很快，修改很慢。看来只能想办法牺牲查询，提高修改效率了。（都变到$log$级别是我们的目标）
具体怎么做？
能想到的办法就是疏松一下$S$数组，“多线程”，不再只成一条链， 成$log$条。这样我们修改的时候，只改其中一条；查询的时候，把这$log$条合并起来。

现学现卖，不愧是你。

---

以上是p话，知道答案怎样推导都没问题。

P.S.下文的$S[i\to j]$代表$a[i]+a[i+1]+\cdots +a[j]$，$S[a]$代表$S[1\to a]$。

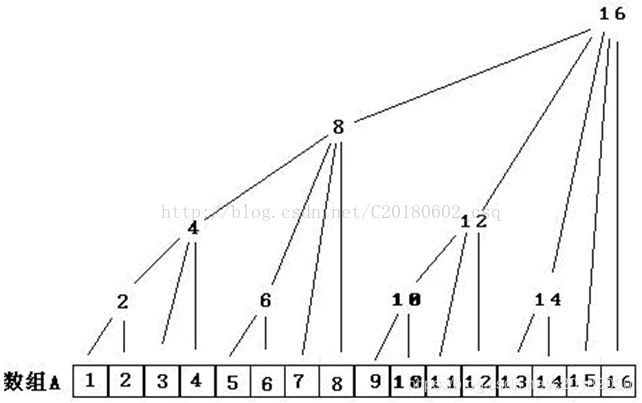
树状数组的思路是把每个数二进制分解，比如$S[27]=S[1\to 16]+S[17\to 24]+S[24\to 26]+S[27\to 27]$。因为$27=16+8+2+1$，所以我们就把$1\to 27$这$27$个数划分为$4$段，长度分别为$16,8,2,1$。

我懂了，然后呢？

于是我们就让$C[16]=S[1\to 16],C[24]=S[17\to 24],C[26]=S[24\to 26],C[27]=S[27\to 27]$。那么$S[27]=C[16]+C[24]+C[26]+C[27]，S[11011]=C[10000]+C[11000]+C[11010]+C[11011]$。
如果你愿意的话，你可以让$C[0]=0$，就有了$S[11011]=C[00000]+C[10000]+C[11000]+C[11010]+C[11011]$。
看后者，多么和谐，$11011\to 11010\to 11000\to 10000\to 00000$。 从$27$开始，每次抹除掉最后一位$1$，即$lowbit$。

我好像发现了规律，C[x]里装的就是S[(x-lowbit(x)+1)~x]的值，然后搜完C[x]之后就看C[x+lowbit(x)]。
然后呢？这些个C是所有的S[x]共用的吗？

我嫖我嫖的CSQ的图哈哈哈哈

那是当然，每个数二进制分解都是$32,16,8,4,2,1$，如果它的最高位是$10000$，还有$1000$这一项的话，就必然会访问到$C[16]$和$C[24]$。

那，你告诉我怎么求C[x]？
你为什么不回答？哈？让我再提一个问题？
我想想……我想想……嗯……
对了，你一直在讲查询，你都没有讲怎么修改。

问得好，因为这两个本质上是一样的。
不带修改的时候，我们会先给出原数组$ar{r}_{1\to n}$，然后求出$S_{1\to n}$。
我们求$C_{1\to n}$的时候，可以将$ar{r}_i$看作将$i$位置上的数从$0$增加了$ar{r}_i$的一次修改操作。

那具体怎么修改呢？
我们每次的修改的形式是将一个$x$位置上的数增加$\Delta$，那么$\Delta$会加到哪些$C[i]$上呢？

我们不妨来看每个$C[i]$会用到哪些$ar{r}_x$。上文已经说过，$C[i]=S[i-lowbit(i)+1\to i]$。一个数$j$会在哪些$i-lowbit(i)+1\to i$里呢？
首先肯定会贡献到$C[j]$。
假设$C[j]$的长度($i-(i-lowbit(i)+1)+1)=lowbit(i)$是2，那么$j$肯定会对以$j-lowbit(j)+1$为左端点，长为$4/8/16/32/\cdots$的区间做贡献。或者说，右端点就是$j+2,j+4,j+8,j+16,\cdots$，即$C[j+2],C[j+4],C[j+8],C[j+16],\cdots$。
我们也可以把这个过程看作$j$不断加上$lowbit(j)$的过程。

---

你到底在说什么？你不是一度的语文年级前几班级第一吗？

那是你那不是我。

那你去找物管啊，不是，去找语文老师补习语文啊。你是不是数论写多了就不会说人话了啊？

---

代码

以下是加。
如果是减就加负数。
如果是修改，那就减去原数，加上新数。

直接网页写的，什么也不保证。

int n,bit[114514];
int lowbit(int x){return x&(-x);}

inline void update(int pos,int del)
{
	while(pos<=n) bit[pos]+=del,pos+=lowbit(pos);
}

inline int getsum(int pos)
{
	int sum=0;
	while(pos) sum+=bit[pos],pos-=lowbit(pos);
	return sum;
}

有板子题树状数组1，代码就不给出了。

区间修改单点查询

分析

单点查询指的是求这个点的值。

差分思想

我们引入一个数组$d[i]=a[i]-a[i-1]$，则有$a[i]={\sum }_{j=1}^{i}d[i]$，这个非常显然。
然后就转换回前缀和问题了。

怎么区间修改呢？
比方说区间加法吧，区间$[l,r]$的数都加上$x$。
如果说$i和i-1$都被修改了，那么$d[i]=(a[i]+x)-(a[i-1]+x)$，是不变的。
唯一会变的就是$l$和$r+1$了，$d[l]=a[l]+x-a[l-1]，d[r+1]=d[r+1]-(d[r]+x)$，$d[l]$它变大了$x$，$d[r+1]$它变小了$x$。
就转换回单点修改问题了。

代码

树状数组方面是一样的。
所以不给。

所以给板子题，洛谷树状数组2的代码，多年前写的，懒得改了。

#include
#include
#include
#include
using namespace std;

void Read(int &p)
{
	p=0;
	int f=1;
	char c=getchar();
	while(c<'0' || c>'9') 
	{
		if(c=='-') f=-1;
		c=getchar();
	}
	while(c>='0' && c<='9')
		p=p*10+c-'0',c=getchar();
	p*=f;
}

#define lowbit(i) ((i)&(-(i)))

const int MAXN=500000+2030;
int N,Q,opt,las,u,v,w,bit[MAXN];

void update(int pos,int del)
{
	while(pos<=N) bit[pos]+=del,pos+=lowbit(pos);
}

int getsum(int pos)
{
	int sum=0;
	while(pos>0) sum+=bit[pos],pos-=lowbit(pos);
	return sum;
}

int main()
{	
	Read(N); Read(Q);
	for(int i=1;i<=N;i++) Read(u),update(i,u-las),las=u;
	while(Q--)
	{
		Read(opt);
		if(opt==1) Read(u),Read(v),Read(w),update(u,w),update(v+1,-w);
		else Read(u),printf("%d\n",getsum(u));
	}
}

区间修改区间查询

分析

我们现在得维护$a$的前缀和了。

$S[n]={\sum }_{i=1}^{n}a[i]={\sum }_{i=1}^n{\sum }_{j=1}^{i}d[j]$。
这好像要$\Theta (n^2)$求了。
换一种思路看，每个$d[j]$出现了几次？
$S[n]=a[1]+a[2]+a[3]+\cdots +a[n]=d[1]+(d[1]+d[2])+(d[1]+d[2]+d[3])+\cdots +(d[1]+d[2]+d[3]+\cdots +d[n])$
显然$d[1]出现了n$次，$d[2]出现了n-1次$，$\cdots$，$d[j]出现了n-j+1次$。所以说${\sum }_{i=1}^{n}a[i]={\sum }_{i=1}^{n}d[i]\ast (n-i+1)$，其中$n$和$1$是常量，可以提出来，所以原式等于$(n+1){\sum }_{i=1}^{n}d[i]-{\sum }_{i=1}^{n}d[i]\ast i$。
所以就可以做了。

代码

板子题 线段树1，代码还是多年前的。

#include
#include
#include
#include
using namespace std;

void Read(int &p)
{
	p=0;
	int f=1;
	char c=getchar();
	while(c<'0' || c>'9') 
	{
		if(c=='-') f=-1;
		c=getchar();
	}
	while(c>='0' && c<='9')
		p=p*10+c-'0',c=getchar();
	p*=f;
}

#define lowbit(i) ((i)&(-(i)))
#define ll long long

const int MAXN=502030;
int N,Q,opt,las,u,v,w;
ll bit[MAXN],cit[MAXN];

void update(int pos,int del)
{
	int key=pos;
	while(pos<=N) bit[pos]+=del,cit[pos]+=1LL*del*key,pos+=lowbit(pos);
}

ll getsum(int pos)
{
	ll sum=0,key=pos;
	while(pos>0) sum+=(key+1)*bit[pos]-cit[pos],pos-=lowbit(pos);
	return sum;
}

int main()
{	
	Read(N); Read(Q);
	for(int i=1;i<=N;i++) Read(u),update(i,u),update(i+1,-u);
	while(Q--)
	{
		Read(opt);
		if(opt==1) Read(u),Read(v),Read(w),update(u,w),update(v+1,-w);
		else Read(u),Read(v),printf("%lld\n",getsum(v)-getsum(u-1));
	}
}

用树状数组维护RMQ

被省略了。
不如线段树。

二维树状数组

单点修改，树状数组套树状数组，简单。
比方说update的时候，外层原本的加法换成内层update，内层update该咋样咋样。

二维前缀和也很简单。
单点修改也很简单。

写一下区间修改区间查询的时候怎么差分。
令$d[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]$，则$a[i][j]={\sum }_{x=1}^i{\sum }_{y=1}^{j}d[x][y]$。
.3
现在要求$$S[n][m]=\sum _{i=1}^n\sum _{j=1}^{m}a[i][j]=\sum _{i=1}^n\sum _{j=1}^m\sum _{x=1}^i\sum$$

参考文献

胡小兔tql
Chanis太强了