计算机图形学（三）——实验三：圆的生成算法

实验三：圆的生成算法

3.1实验目的

（1）了解DDA算法、中点画圆法、Bresenham算法
（2）掌握VC++中CDC类的用法

3.2实验内容

（1）类的编写
（2）完成DDA算法、中点画圆法、Bresenham算法

3.3算法思路

在平面解析几何中，圆的方程可以描述为(x–x0)2+(y–y0)2=R2，其中(x0,y0)是圆心坐标，R是圆的半径，特别的，当(x0,y0)就是坐标中心点时，圆方程可以简化为x2+y2=R2。在计算机图形学中，圆和直线一样，也存在点阵输出设备上显示或输出的问题，因此也需要一套光栅扫描转换算法。为了简化，我们先考虑圆心在原点的圆的生成，对于中心不是原点的圆，可以通过坐标的平移变换获得相应位置的圆。
在进行扫描转换之前，需要了解一个圆的特性，就是圆的八分对成性。如下图所示：
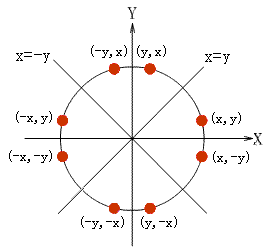圆心位于原点的圆有四条对称轴x=0、y=0、x=y和x=-y，若已知圆弧上一点P(x，y)，就可以得到其关于四条对称轴的七个对称点：（x,-y）、（-x,y）、（-x,-y）、（y,x）、（y,-x）、（-y,x）、（-y,-x），这种性质称为八分对称性。因此只要能画出八分之一的圆弧，就可以利用对称性的原理得到整个圆。
有几种较容易的方法可以得到圆的扫描转换，首先介绍一下直角坐标法。已知圆方程：x2+y2=R2，若取x作为自变量，解出y。
在生成圆时先扫描转换四分之一的圆周，让自变量x从0到R以单位步长增加，在每一步时可解出y，然后调用画点函数即可逐点画出圆。但这样做，由于有乘方和平方根运算，并且都是浮点运算，算法效率不高。而且当x接近R值时(圆心在原点)，在圆周上的点（R，0）附近，由于圆的斜率趋于无穷大，因浮点数取整需要四舍五入的缘故，使得圆周上有较大的间隙。接下来介绍一下极坐标法，假设直角坐标系上圆弧上一点P(x，y)与x轴的夹角是θ，则圆的极坐标方程为：
x=Rcosθ
y=Rsinθ
生成圆是利用圆的八分对称性，使自变量θ的取值范围为(0，45°)就可以画出整圆。
（1）角度数值微分法（DDA法）：
直角坐标系的圆的参数方程为：
{█(x=x0+Rcosθ@y=y0+Rsinθ)┤
由上式导出
x-xc=-Rsinθdθ
y-yc=Rcosθdθ
当x-xc从-r到r做加1递增时，就可以求出对应的圆周点的y坐标。但是这样求出的圆周上的点是不均匀的，| x-xc | 越大，对应生成圆周点之间的圆周距离也就越长。因此，所生成的圆不美观。
（2）中点画圆法：
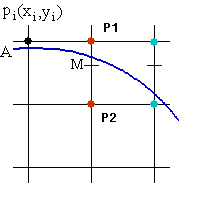
考虑圆心在原点，半径为R的圆在第一象限内的八分之一圆弧，从点（0,R）到点（R/,R/）顺时针方向确定这段圆弧。假定某点Pi(xi,yi)已经是该圆弧上最接近实际圆弧的点，那么Pi的下一个点只可能是正右方的P1或右下方的P2两者之一，如下图所示：
构造判别函数：
F(x,y）=x2+y2–R2
当F(x,y）=0，表示点在圆上，当F(x,y）>0，表示点在圆外，当F(x,y）<0，表示点在圆内。如果M是P1和P2的中点，则M的坐标是（xi+1,yi–0.5），当F（xi+1,yi–0.5）<0时，M点在圆内，说明P1点离实际圆弧更近，应该取P1作为圆的下一个点。同理分析，当F（xi+1,yi–0.5）>0时，P2离实际圆弧更近，应取P2作为下一个点。当F（xi+1,yi–0.5）=0时，P1和P2都可以作为圆的下一个点，算法约定取P2作为下一个点。
（3）Bresenham画圆算法：
如果能将判别式规约到整数运算，则可以简化计算，提高效率。于是人们针对中点画圆法进行了多种改进，其中一种方式是将d的初始值由1.25–R改成1–R，考虑到圆的半径R总是大于2，因此这个修改不会响d的初始值的符号，同时可以避免浮点运算。还有一种方法是将d的计算放大两倍，同时将初始值改成3–2R，这样避免了浮点运算，乘二运算也可以用移位快速代替，采用3–2R为初始值的改进算法，又称为Bresenham算法。

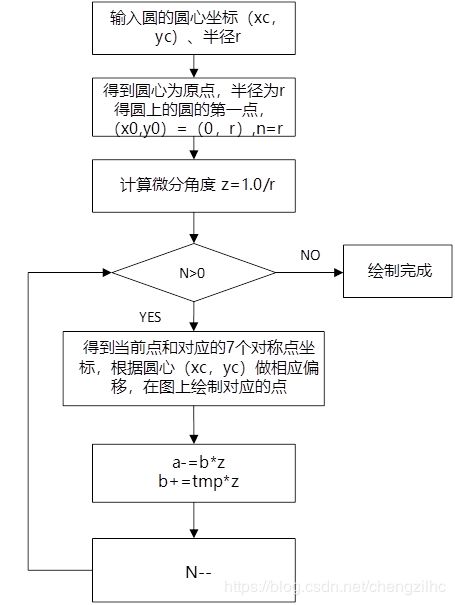
3.4流程图

（1）角度数值微分法（DDA法）：
（2）中点画圆法：
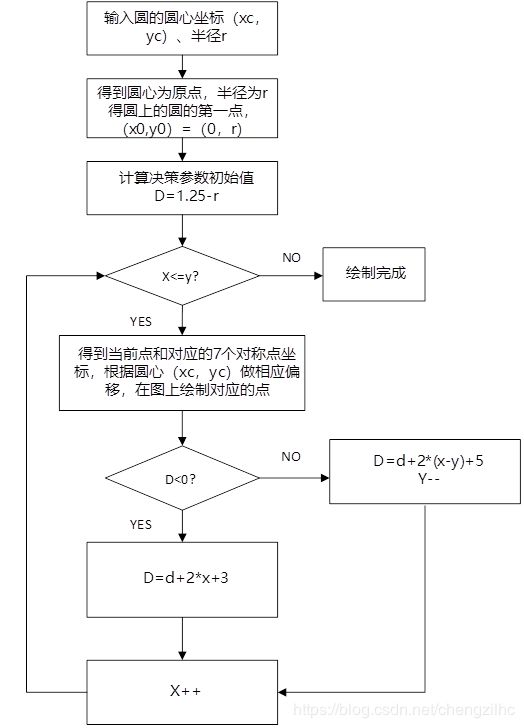（3）Bresenham画圆算法：

3.5实验步骤

（1）角度数值微分法（DDA法）：
直角坐标系的圆的参数方程为：
{█(x=x0+Rcosθ@y=y0+Rsinθ)┤
由上式导出
x-xc=-Rsinθdθ
y-yc=Rcosθdθ
推导：
xn+1=xn-（yn-y0）dθ
yn+1=yn-（xn-x0）dθ
（2）中点画圆法：
1）构造判别函数：F(x,y）=x2+y2–R2。
当F(x,y）=0，表示点在圆上，当F(x,y）>0，表示点在圆外，当F(x,y）<0，表示点在圆内。
如果M是P1和P2的中点，则M的坐标是（xi+1,yi–0.5），当F（xi+1,yi–0.5）<0时，M点在圆内，说明P1点离实际圆弧更近，应该取P1作为圆的下一个点。
同理分析，当F（xi+1,yi–0.5）>0时，P2离实际圆弧更近，应取P2作为下一个点。当F（xi+1,yi–0.5）=0时，P1和P2都可以作为圆的下一个点，算法约定取P2作为下一个点。
2）将M点坐标（xi+1,yi–0.5）带入判别函数F(x,y），得到判别式d：
d=F（xi+1,yi–0.5）=(xi+1)2+(yi–0.5)2–R2
3）若d<0，则取P1为下一个点，此时P1的下一个点的判别式为：
d’=F（xi+2,yi–0.5）=(xi+2)2+(yi–0.5)2–R2
展开后将d带入可得到判别式的递推关系：
d’=d+2xi+3
若d>0，则取P2为下一个点，此时P2的下一个点的判别式为：
d’=F（xi+2,yi–1.5）=(xi+2)2+(yi–1.5)2–R2
展开后将d带入可得到判别式的递推关系：
d’=d+2(xi-yi)+5
4）特别的，在第一个象限的第一个点（0,R）时，可以推倒出判别式d的初始值d0：
d0=F(1,R–0.5)=1–(R–0.5)2–R2=1.25-R
考虑到圆心不在原点的情况，需要对计算出来的坐标进行平移。
（3）Bresenham画圆算法：
1）构造判别函数：F(x,y）=x2+y2–R2。
当F(x,y）=0，表示点在圆上，当F(x,y）>0，表示点在圆外，当F(x,y）<0，表示点在圆内。
如果M是P1和P2的中点，则M的坐标是（xi+1,yi–0.5），当F（xi+1,yi–0.5）<0时，M点在圆内，说明P1点离实际圆弧更近，应该取P1作为圆的下一个点。
同理分析，当F（xi+1,yi–0.5）>0时，P2离实际圆弧更近，应取P2作为下一个点。当F（xi+1,yi–0.5）=0时，P1和P2都可以作为圆的下一个点，算法约定取P2作为下一个点。
2）将M点坐标（xi+1,yi–0.5）带入判别函数F(x,y），得到判别式d：
d=F（xi+1,yi–0.5）=(xi+1)2+(yi–0.5)2–R2
3）若d<0，则取P1为下一个点，此时P1的下一个点的判别式为：
d’=F（xi+2,yi–0.5）=(xi+2)2+(yi–0.5)2–R2
展开后将d带入可得到判别式的递推关系：
d’=d+4xi+6
若d>0，则取P2为下一个点，此时P2的下一个点的判别式为：
d’=F（xi+2,yi–1.5）=(xi+2)2+(yi–1.5)2–R2
展开后将d带入可得到判别式的递推关系：
d’=d+4(xi-yi)+10
4）特别的，在第一个象限的第一个点（0,R）时，可以推倒出判别式d的初始值d0：
d0=F(1,R–0.5)=1–(R–0.5)2–R2=3-2R
考虑到圆心不在原点的情况，需要对计算出来的坐标进行平移。

3.6实验代码

（1）角度DDA圆生成算法

/////////////////////////////////////////////////////////////////////////////
//角度DDA圆生成算法
/////////////////////////////////////////////////////////////////////////////
void CLiHuchenView::OnDdacircle() 
{
	// TODO: Add your command handler code here
	CDC *pDC=GetDC();//获取设备指针
	int xc=200,yc=200,r=50,c=RGB(0,0,255);///定义圆心,角度，半径，圆的颜色蓝色
    int x=0,y=r,n=r; //赋初值
	double rc = (double)r; //修改类型
    double z=1.0/rc; //得到微分角度
    double a=x,b=y; //将x，y分别赋予a，b
    double tmp; //定义变量
    while(n > 0)
	{
		//八个区域点，画点
	    pDC->SetPixel((xc+x),(yc+y),c);//(x,y)
     	pDC->SetPixel((xc-x),(yc+y),c);//(-x,y)
	    pDC->SetPixel((xc+x),(yc-y),c);//(x,-y)
    	pDC->SetPixel((xc-x),(yc-y),c);//(-x,-y)
    	pDC->SetPixel((xc+y),(yc+x),c);//(y,x)
    	pDC->SetPixel((xc-y),(yc+x),c);//(-y,x)
    	pDC->SetPixel((xc+y),(yc-x),c);//(y,-x)
    	pDC->SetPixel((xc-y),(yc-x),c);//(-y,-x)

        tmp=a;
        a-=b*z; //计算下一点横坐标
        b+=tmp*z; //计算下一点纵坐标
        x = (int)(a);
        y = (int)(b);
        n--;
	}
    if(x == y)
	{
		//八个区域点，画点
        pDC->SetPixel((xc+x),(yc+y),c);//(x,y)
     	pDC->SetPixel((xc-x),(yc+y),c);//(-x,y)
	    pDC->SetPixel((xc+x),(yc-y),c);//(x,-y)
    	pDC->SetPixel((xc-x),(yc-y),c);//(-x,-y)
    	pDC->SetPixel((xc+y),(yc+x),c);//(y,x)
    	pDC->SetPixel((xc-y),(yc+x),c);//(-y,x)
    	pDC->SetPixel((xc+y),(yc-x),c);//(y,-x)
    	pDC->SetPixel((xc-y),(yc-x),c);//(-y,-x)
	}
	
	ReleaseDC(pDC);//指针释放
}

（2）中点圆生成算法：

/////////////////////////////////////////////////////////////////////////////
//中点圆生成算法
/////////////////////////////////////////////////////////////////////////////
void CLiHuchenView::OnMidpointcircle() 
{
	// TODO: Add your command handler code here
	CDC *pDC=GetDC();//获取设备指针
	int xc=300,yc=300,r=50,c=RGB(255,0,0);///定义圆心，半径，圆的颜色红色
	int x,y;//定义变量x，y
	float d;//定义中点带入圆的值d
	x=0;y=r;d=1.25-r;//赋初值

	//八个区域点，画点
    pDC->SetPixel((xc+x),(yc+y),c);//(x,y)
	pDC->SetPixel((xc-x),(yc+y),c);//(-x,y)
	pDC->SetPixel((xc+x),(yc-y),c);//(x,-y)
	pDC->SetPixel((xc-x),(yc-y),c);//(-x,-y)
	pDC->SetPixel((xc+y),(yc+x),c);//(y,x)
	pDC->SetPixel((xc-y),(yc+x),c);//(-y,x)
	pDC->SetPixel((xc+y),(yc-x),c);//(y,-x)
	pDC->SetPixel((xc-y),(yc-x),c);//(-y,-x)

	//画圆
	while(x<=y)
	{
		//判断d的正负
		if(d<0)
		{
			d+=2*x+3;
		}
		else
		{
			d+=2*(x-y)+5;
			y--;
		}
		x++;
	    pDC->SetPixel((xc+x),(yc+y),c);//(x,y)
     	pDC->SetPixel((xc-x),(yc+y),c);//(-x,y)
	    pDC->SetPixel((xc+x),(yc-y),c);//(x,-y)
    	pDC->SetPixel((xc-x),(yc-y),c);//(-x,-y)
    	pDC->SetPixel((xc+y),(yc+x),c);//(y,x)
    	pDC->SetPixel((xc-y),(yc+x),c);//(-y,x)
    	pDC->SetPixel((xc+y),(yc-x),c);//(y,-x)
    	pDC->SetPixel((xc-y),(yc-x),c);//(-y,-x)
	}
	ReleaseDC(pDC);//指针释放
}

（3）Bresenham圆生成算法：

/////////////////////////////////////////////////////////////////////////////
//Bresenham圆生成算法
/////////////////////////////////////////////////////////////////////////////
void CLiHuchenView::OnBresenhamcircle() 
{
	// TODO: Add your command handler code here
	CDC *pDC=GetDC();//获取设备指针
	int xc=100,yc=100,r=50,c=RGB(0,255,0);///定义圆心，半径，圆的颜色绿色
	int x=0,y=r,p=3-2*r;//赋初值

	//画圆
	while(x<y)
	{
		//八个区域点，画点
        pDC->SetPixel((xc+x),(yc+y),c);//(x,y)
    	pDC->SetPixel((xc-x),(yc+y),c);//(-x,y)
    	pDC->SetPixel((xc+x),(yc-y),c);//(x,-y)
    	pDC->SetPixel((xc-x),(yc-y),c);//(-x,-y)
    	pDC->SetPixel((xc+y),(yc+x),c);//(y,x)
    	pDC->SetPixel((xc-y),(yc+x),c);//(-y,x)
    	pDC->SetPixel((xc+y),(yc-x),c);//(y,-x)
    	pDC->SetPixel((xc-y),(yc-x),c);//(-y,-x)

		//判断p的正负
		if(p<0)
		{
			p+=4*x+6;
		}
		else
		{
			p+=4*(x-y)+10;
			y--;
		}
		x++;
		if(x==y)
	    pDC->SetPixel((xc+x),(yc+y),c);//(x,y)
     	pDC->SetPixel((xc-x),(yc+y),c);//(-x,y)
	    pDC->SetPixel((xc+x),(yc-y),c);//(x,-y)
    	pDC->SetPixel((xc-x),(yc-y),c);//(-x,-y)
    	pDC->SetPixel((xc+y),(yc+x),c);//(y,x)
    	pDC->SetPixel((xc-y),(yc+x),c);//(-y,x)
    	pDC->SetPixel((xc+y),(yc-x),c);//(y,-x)
    	pDC->SetPixel((xc-y),(yc-x),c);//(-y,-x)
	}
	ReleaseDC(pDC);//指针释放	
}

3.7实验结果展示

红色：中点画线算法
绿色： Bresenham算法
蓝色：角度微分法（DDA法）